قطر الدائرة المحددة للمثلث. ملخص الدرس "الدائرة المحددة". كيفية إيجاد نصف قطر دائرة حول مثلث - الصيغة العامة
في هذا الجزء ، سنناقش الدائرة المقيدة حول (غالبًا ما يُقال "بالقرب") من المثلث. بادئ ذي بدء ، دعنا نعطي تعريفًا.
1. وجود ومركز الدائرة المحصورة
هنا السؤال الذي يطرح نفسه: هل توجد مثل هذه الدائرة لأي مثلث؟ اتضح أن نعم ، للجميع. علاوة على ذلك ، سنقوم الآن بصياغة نظرية تجيب أيضًا على السؤال ، أين يقع مركز الدائرة المحددة.
صيغ لإيجاد طول قطر المستطيل
صيغة على جانب مستطيل في القطر والزاوية β. يطلق عليه اسم قطري المستطيل لأي جزء يربط رأسين من زوايا متقابلة من المستطيل. صيغة قطر المستطيل بدلالة ضلعي المستطيل.
صيغة قطر المستطيل في المساحة وعلى كلا الجانبين. صيغة قطر المستطيل على طول المحيط وعلى كلا الجانبين. صيغة قطر المستطيل بدلالة نصف قطر الدائرة المحصورة. صيغة قطر المستطيل على طول محيط الدائرة.
يبدو مثل هذا:
دعونا نحشد الشجاعة ونثبت هذه النظرية. إذا كنت قد قرأت بالفعل موضوع "" ، واكتشفت سبب تقاطع المنشورات الثلاثة في نقطة واحدة ، فسيكون ذلك أسهل بالنسبة لك ، ولكن إذا لم تكن قد قرأته ، فلا تقلق: الآن سنكتشف كل شيء خارج.
سنقوم بإجراء الإثبات باستخدام مفهوم موضع النقاط (LPT).
صيغة قطر المستطيل بدلالة جيب الزاوية المجاورة للقطر وطول الضلع المقابل لتلك الزاوية. صيغة قطر المستطيل بدلالة جيب تمام الزاوية المجاورة للقطر وطول الضلع المجاور لتلك الزاوية. صيغة قطر المستطيل بدلالة جيب الزاوية الحادة بين الأقطار ومساحة المستطيل.
صيغ لتحديد طول محيط المستطيل
يسمى محيط المستطيل بمجموع أطوال جميع جوانب المستطيل. صيغة محيط المستطيل بدلالة ضلعي المستطيل. صيغة محيط المستطيل بمعلومية المساحة والجانبين. صيغة محيط المستطيل على طول القطر وعلى كلا الجانبين.
حسنًا ، على سبيل المثال ، هل مجموعة الكرات "مكان هندسي" للأجسام المستديرة؟ لا ، بالطبع ، لأن هناك بطيخ دائري. ولكن هل مجموعة من الناس ، "مكان هندسي" ، قادرة على الكلام؟ لا ، لأن هناك أطفالاً لا يستطيعون الكلام. في الحياة ، من الصعب عمومًا العثور على مثال حقيقي "لمكان هندسي للنقاط". الهندسة أسهل. هنا ، على سبيل المثال ، هو فقط ما نحتاجه:
صيغة محيط المستطيل بدلالة نصف قطر الدائرة المقيدة وعلى كلا الجانبين. صيغة محيط المستطيل بمعلومية قطر الدائرة المحصورة وكلا الجانبين. تسمى مساحة المستطيل في المساحة التي تحدها جوانب المستطيل ، أي داخل منطقة محيط المستطيل.
صيغ تحديد مساحة المستطيل
صيغة لمساحة المستطيل ذي الجانبين. صيغة مساحة المستطيل على طول المحيط وعلى كلا الجانبين. صيغة مساحة المستطيل على طول القطر وعلى كلا الجانبين. صيغة مساحة المستطيل على طول القطر وجيب الزاوية الحادة بين الأقطار.
هنا تكون المجموعة هي المنتصف عموديًا ، وتكون الخاصية "" هي "أن تكون على مسافة متساوية (نقطة) من نهايات المقطع."
دعونا تحقق؟ لذلك ، عليك التأكد من أمرين:
تواصل مع ومع. ثم الخط هو الوسيط والارتفاع في. لذلك ، - متساوي الساقين ، - تأكدنا من أن أي نقطة ملقاة على المنصف العمودي تكون بعيدة بنفس القدر عن النقاط و.
دائرة يحدها مستطيل
صيغة مساحة المستطيل بمعلومية نصف قطر الدائرة المحصورة وأي جانب. صيغة مساحة المستطيل في الدائرة هي دائرة على كلا الجانبين. تسمى الدائرة المحددة حول المستطيل ، بدائرة تمر عبر الرؤوس الأربعة للمستطيل ، مركزها تقاطع أقطار المستطيل.
صيغ لإيجاد نصف قطر دائرة مقيدة حول مستطيل
صيغة نصف قطر الدائرة التي يحدها مستطيل من ضلعين. صيغة نصف قطر الدائرة المحصورة حول مستطيل على طول محيط المربع وأي من الضلعين. وصف صيغة نصف قطر الدائرة حول المستطيل بدلالة مساحة المستطيل وطول أحد أضلاعه.
خذ - الوسط واتصل و. حصلت على الوسيط. لكن - متساوي الساقين حسب الشرط ، ليس فقط الوسيط ، ولكن أيضًا الارتفاع ، أي المتوسط العمودي. هذا يعني أن النقطة تقع بالضبط على المنصف العمودي.
الجميع! لقد تحققنا تمامًا من حقيقة أن المنصف العمودي على مقطع ما هو موضع النقاط على مسافة متساوية من نهايات المقطع.
صيغة نصف قطر الدائرة المُحددة حول مستطيل بامتداد قطر المستطيل. معادلة نصف قطر الدائرة الموصوفة حول المستطيل بالقطر المحيطي للدائرة. صيغة نصف قطر الدائرة الموصوفة حول المستطيل بدلالة جيب الزاوية المجاورة للقطر وطول الضلع المقابل لهذه الزاوية.
الدائرة المحيطة بالمضلع المحدد هي الدائرة المقيدة. سمع معظم الناس المصطلحين محيط ونصف قطر ، لكن الدائرة المحدودة هي مصطلح أقل شيوعًا. تخيل مضلعًا ثنائي الأبعاد بجوانب مستقيمة ، مثل المثلث. تخيل دائرة حول مثلث بحيث يلامس رؤوسه الثلاثة ؛ إنها دائرة محدودة. لحساب نصف قطرك ، ما عليك سوى استخدام بعض الجبر البسيط والآلة الحاسبة.
كل هذا جيد وجيد ، لكن هل نسينا الدائرة المقيدة؟ لا على الإطلاق ، لقد أعددنا أنفسنا للتو "رأس جسر للهجوم".
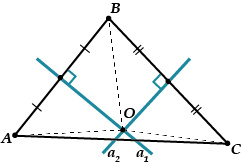
فكر في مثلث. لنرسم عمودين متوسطين ، ولنقل ، على المقاطع و. سوف يتقاطعون في مرحلة ما ، والتي سنسميها.
تحقق من جميع قياساتك وتأكد من أن البوصلة تشير إلى أنها لا تتغير أثناء الدوران.
- من المهم للغاية القياس بدقة ودقة.
- لا يمكن أن تحتوي كل المضلعات على دائرة محددة.
وبالتالي ، فإن مساحة الدائرة المنقوشة في شكل سداسي تساوي. الآن ننتقل إلى المربع المنقوش. بما أن قطر المربع يساوي ضلع جذر ضرب المثلثات ، فلدينا. ثم نصف قطر الدائرة المدرجة في مربع سيكون له نصف قياس ضلعها. وهكذا ، سترى أن نصف قطر الدائرة المدرجة في المثلث هو نصف نصف قطر الدائرة المحاطة بمثلث ، لأن محيط الدائرة موصوف بوسط مقسم إلى جزأين يتناسبان مع 1 ، ثم نصف القطر سيكون من الدائرة المنقوشة.
والآن الانتباه!
النقطة تقع على المنصف العمودي ؛
النقطة تقع على المنصف العمودي.
وهذا يعني و.
عدة أشياء تتبع من هذا:
أولاً، يجب أن تقع النقطة على المنصف العمودي الثالث ، على المقطع.
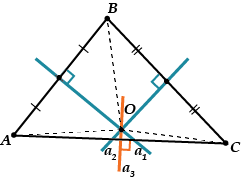
قياس الدائرة وتقريبها
وبالتالي ، ستكون مساحة الدائرة المنقوشة. والمشكلة هي إثبات أن مجموع هذه المساحات يساوي مساحة الدائرة الداخلية. لذا ، دعونا نحسب مجموع مساحات التيجان. هذا هو مجموع مناطق التيجان. يمكنك أن ترى أن لدينا 3 دوائر من الأشعة. تقترح هذه المقالة فرضية ، ذريعة للنظر في بعض النقاط في رياضيات هذه الفترة في بلاد ما بين النهرين.
من خلال تشكيل دائرة بين شكلين سداسيين ، يمكن حساب محيطهما بسهولة ، ثم مضاعفة عدد الأضلاع على التوالي ، يحصل على إطار به مضلعات من 96 جانبًا. ربما يكون من الأسهل تقييم الأداء من خلال تحديد القيم الرقمية.
وهذا يعني أن المنصف العمودي يجب أن يمر أيضًا بالنقطة ، وتتقاطع جميع المنصات الثلاثة المتعامدة عند نقطة واحدة.
ثانيًا: إذا رسمنا دائرة مركزها عند نقطة ونصف قطر ، فستمر هذه الدائرة أيضًا بالنقطة وعبر النقطة ، أي ستكون الدائرة المحددة. هذا يعني أنه موجود بالفعل أن تقاطع المنصفات الثلاثة المتعامدة هو مركز الدائرة المقيدة لأي مثلث.
نرى هنا فائدة وفعالية أساليب المراقبة: من ناحية ، توفر تقريبيًا ، ومن ناحية أخرى ، تسمح لك بالتحكم في خطأ كامل. وبقدر ما أعلم ، فإن أرخميدس هو أول من يبرر صراحة نتائجه فيما يتعلق بالدائرة ، ويعطي خطوة بخطوة سلسلة من الحجج التي تشرح سبب صحة ما يدعيه. لكنه ليس أول من يهتم بالدائرة وقياسها. لدينا أدلة قديمة جدًا ، واحدة في مصر والبعض الآخر في بلاد ما بين النهرين ، تسير في هذا الاتجاه.
وهناك بعض الألواح الطينية "البابلية" التي تعود إلى نفس الفترة وعلى طول محيط أو مساحة القرص. هذا هو موضوع هذا المقال. يمكن أن تبدأ المسيرة ولكن قبل المغادرة إلى بابل في القرنين السابع عشر والثامن عشر قبل الميلاد. تم العثور على لوح طيني بابلي يعطي نسبة محيط الشكل السداسي إلى محيط دائرته المحددة.
وآخر شيء: عن التفرد. من الواضح (تقريبًا) أنه يمكن الحصول على النقطة بطريقة فريدة ، وبالتالي فإن الدائرة فريدة أيضًا. حسنًا ، "تقريبًا" - سنترك الأمر لك. هنا أثبتنا النظرية. يمكنك أن تصرخ "مرحى!".
وإذا كانت المشكلة هي السؤال "أوجد نصف قطر الدائرة المحددة"؟ أو بالعكس ، يتم إعطاء نصف القطر ، لكنك بحاجة إلى العثور على شيء آخر؟ هل هناك معادلة تربط نصف قطر الدائرة المحددة بعناصر أخرى في المثلث؟
وغالبًا ما يتم إضافتهم بشكل أو بآخر. كانت هذه هي الثانية التي أعطتني مشكلة: هل يستطيع البابليون حقًا العثور على هذه القيمة من خلال التجربة؟ حاليًا ، التجربة سهلة الاستخدام ، مع مقياس خياطة وأشياء يومية بأقطار مختلفة: مقلاة ، قدر ، علب من الصفيح. يتم قياس المحيط والقطر ويتم إجراء التقسيم. كانت الاختلافات في المكان العشري الثالث. بالطبع ، لا توجد مثل هذه العناصر الصناعية الدقيقة ، ولا توجد عدادات للخياطة متدرجة بالمليمترات.
للقياس ، يكون أرق: حبل ، حزام جلدي ، يمكن أن يمتد تحت التوتر ويتقلص بسهولة. من ناحية أخرى ، لا يطول لحاء البردى المجفف. لسوء الحظ ، لم يكن لدي. من الواضح أنهم لم يتخرجوا ، لكن هذا ليس خطيرًا: نحن مهتمون بنسبة طولين: من المحيط والقطر ، وليس من الأطوال نفسها. من السهل الالتفاف حول كائن مع الروطان وقطعه. من الغريب أنه ليس من السهل قطع خيط الروطان بدقة لمطابقة القطر. في الواقع ، غالبًا ما يتم تقريب الحافة العلوية للفخار.
في كثير من الأحيان ، عند حل المشكلات الهندسية ، يتعين عليك تنفيذ إجراءات بأشكال مساعدة. على سبيل المثال ، ابحث عن نصف قطر دائرة منقوشة أو مقيدة ، إلخ. ستوضح لك هذه المقالة كيفية العثور على نصف قطر دائرة تحيط بمثلث. أو بعبارة أخرى ، نصف قطر الدائرة المدرج فيها المثلث.
لذلك ، من الضروري تثبيت الروطان حول المحيط ، ثم قطع سكين الروطان الثاني ، المقابل للقطر الداخلي للقطر الأول. يبقى حساب نسبة الطولين دون معرفتهما القيم الدقيقة، والذي يمكن القيام به من خلال العودة إلى أصل الانقسام. 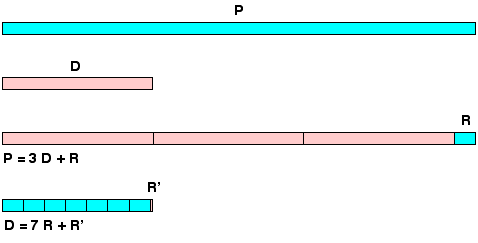
كان أفضل أداء لي هو 6 ، 8 مرات ، أي 6 مرات ، مع راحة رائعة. ومع ذلك ، أقنعتني هذه التجارب أن البابليين لم يتلقوا قيمة تجريبية ، على الأقل ليس من هذا الطريق. لكن في هذه الحالة ، ينشأ سؤالان.
كيفية إيجاد نصف قطر دائرة حول مثلث - الصيغة العامة
الصيغة العامة هي كما يلي: R = abc / 4√p (p - a) (p - b) (p - c) ، حيث R هو نصف قطر الدائرة المحصورة ، p هو محيط المثلث مقسومًا على 2 (نصف محيط). أ ، ب ، ج هي أضلاع المثلث.
أوجد نصف قطر دائرة المثلث إذا كانت أ = 3 ، ب = 6 ، ج = 7.
السؤال الأول: إذا لم يكن تجريبيًا فهو نظري وهندسي. 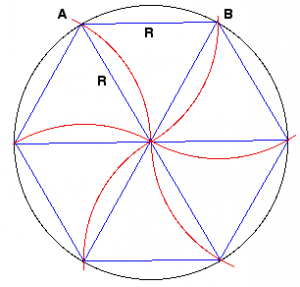
وهكذا ، فإن محيط الدائرة أكبر من محيط الشكل السداسي ، والنسبة بينهما متساوية. من الطبيعي جدًا أن نقدر محيط دائرة ، غير معروف بالنسبة إلى ما هو معروف عن الشكل السداسي نفسه.
في وقت لاحق سوف نرى ما يجب التفكير فيه. الفرضية الأولى: عرف البابليون نظرية فيثاغورس قبل ألف عام. الفرضية 2: كانوا يعرفون أنهم وجدوا مستطيلات ذات جوانب صحيحة. ربما ليس كل شيء ، ولكن على الأقل أولئك الذين يكون الوتر وأحد أضلاعه أعدادًا صحيحة.
وبالتالي ، بناءً على الصيغة أعلاه ، نحسب شبه المحيط:
ع = (أ + ب + ج) / 2 = 3 + 6 + 7 = 16. => 16/2 = 8.
استبدل القيم الموجودة في الصيغة واحصل على:
R = 3 × 6 × 7 / 4√8 (8-3) (8-6) (8-7) = 126 / 4√ (8 × 5 × 2 × 1) = 126/4√80 = 126/16 √5.
الجواب: R = 126 / 16-5
كيفية إيجاد نصف قطر دائرة حول مثلث متساوي الأضلاع
لإيجاد نصف قطر دائرة حول مثلث متساوي الأضلاع ، توجد صيغة بسيطة إلى حد ما: R = a / √3 ، حيث a هو حجم جانبها.
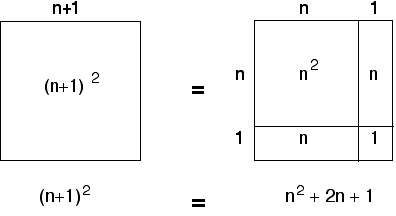
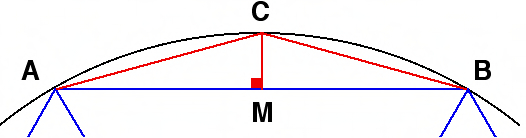
بالطبع ، لا يوجد دليل على أن البابليين فعلوا ذلك. فقط اكتشاف لوح طيني جديد يمكنه القيام بذلك. علاوة على ذلك ، تستند هذه الفكرة إلى الفرضيات 1 وهل عرف البابليون حقًا كيفية إيجاد مثل هذه المثلثات؟ 
تم تقسيم آخر 15 سطرًا إلى 4 أعمدة ، يحدد أول سطرين المحتوى. يحتوي العمود 4 على العلامة متبوعة بالأرقام من 1 إلى.
مثال: ضلع مثلث متساوي الأضلاع هو 5. أوجد نصف قطر الدائرة المحصورة.
نظرًا لأن جميع جوانب المثلث متساوي الأضلاع متساوية ، لحل المشكلة ، ما عليك سوى إدخال قيمته في الصيغة. نحصل على: R = 5 / √3.
الجواب: R = 5 / √3.
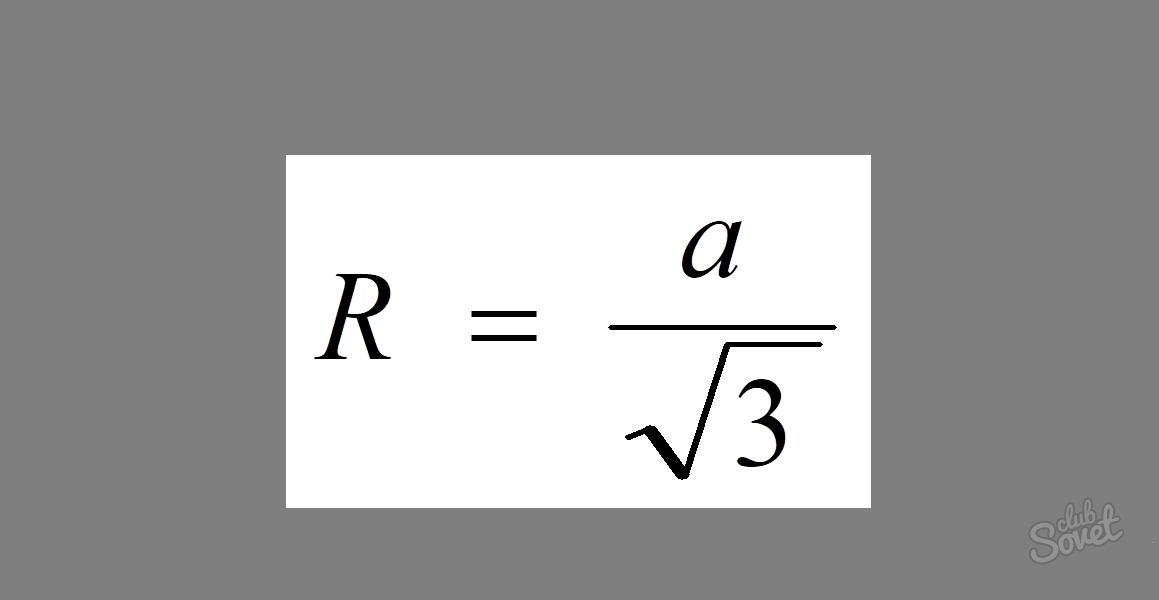
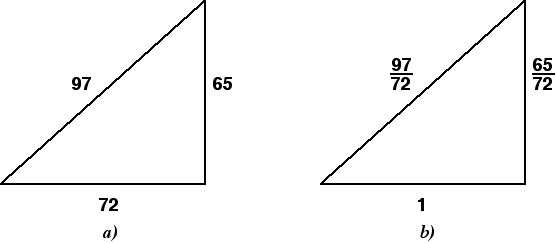
كيفية إيجاد نصف قطر دائرة حول مثلث قائم الزاوية
تبدو الصيغة كما يلي: R = 1/2 × √ (a² + b²) = c / 2 ، حيث a و b ساقان و c هو الوتر. إذا أضفنا مربعات الأرجل في مثلث قائم الزاوية ، نحصل على مربع الوتر. كما يتضح من الصيغة ، هذا التعبير موجود تحت الجذر. بحساب جذر تربيع الوتر ، نحصل على الطول نفسه. يؤدي ضرب التعبير الناتج بمقدار 1/2 في النهاية إلى التعبير 1/2 × c = c / 2.
تشير الأعمدة 1 و 2 و 3 إلى مثلثات قائمة. يعطي العمودان 2 و 3 على التوالي أصغر ضلع ووتر لكل مثلث. يعطي العمود 1 مربع النسبة على جانبي الزاوية اليمنى. على سبيل المثال ، السطر 5 يبدأ في النظام الجنسي.
هذا دقيق جدًا لدرجة يصعب تصديقه ، لكن يمكنك التحقق من أنه متماثل مع السلاسل الأخرى. هناك جدل حول الأساليب التي ربما استخدمها البابليون لتجميع هذا الجدول. هناك أيضًا أخطاء في نسخة الكاتب وألغاز صغيرة ، مثل السطر 11 الذي يعطي 45 و 1 15 كضلع ، أي في الترقيم العشري: 45 ، وكلاهما من مضاعفات الرقم 15 ، وهذا المثلث ليس سوى مثلث من الجانبين. لماذا لم يتم تقديمها بهذا الشكل ، أبسط من ذلك بكثير؟ وما هي ميزة إعطاء مربع المنحدر بدلاً من المنحدر نفسه؟
مثال: احسب نصف قطر الدائرة المحصورة إذا كانت أرجل المثلث 3 و 4. عوض بالقيم في الصيغة. نحصل على: R = 1/2 × √ (3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2.5.
في هذا التعبير ، 5 هو طول الوتر.
الجواب: R = 2.5.
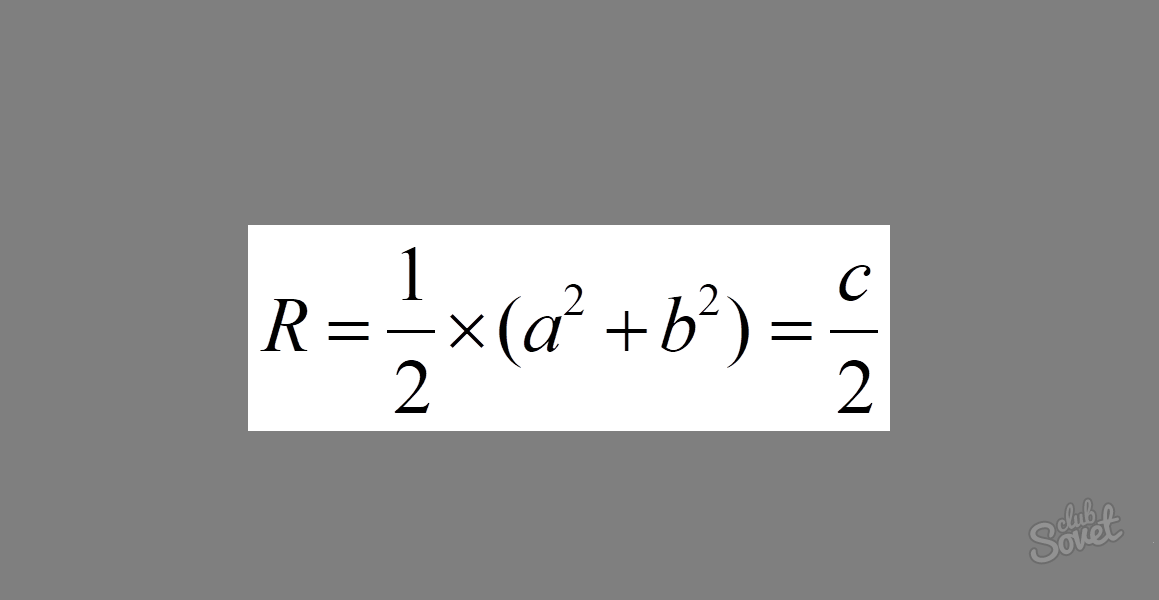
كيفية إيجاد نصف قطر دائرة حول مثلث متساوي الساقين
تبدو الصيغة كما يلي: R = a² / √ (4a² - b²) ، حيث a هو طول فخذ المثلث و b طول القاعدة.
مثال: احسب نصف قطر دائرة إذا كان وركها = 7 وقاعدتها = 8.
الحل: نحن نستبدل هذه القيم في الصيغة ونحصل على: R \ u003d 7² / √ (4 × 7² - 8²).
R = 49 / √ (196-64) = 49 / √132. يمكن كتابة الجواب مباشرة مثل هذا.
الجواب: R = 49 / √132
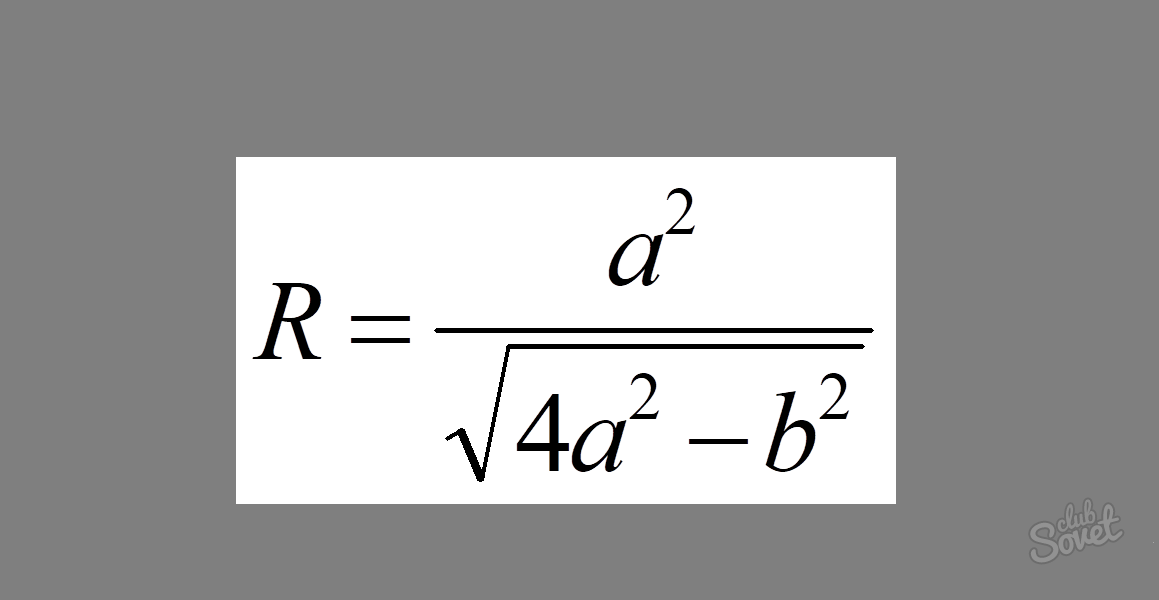
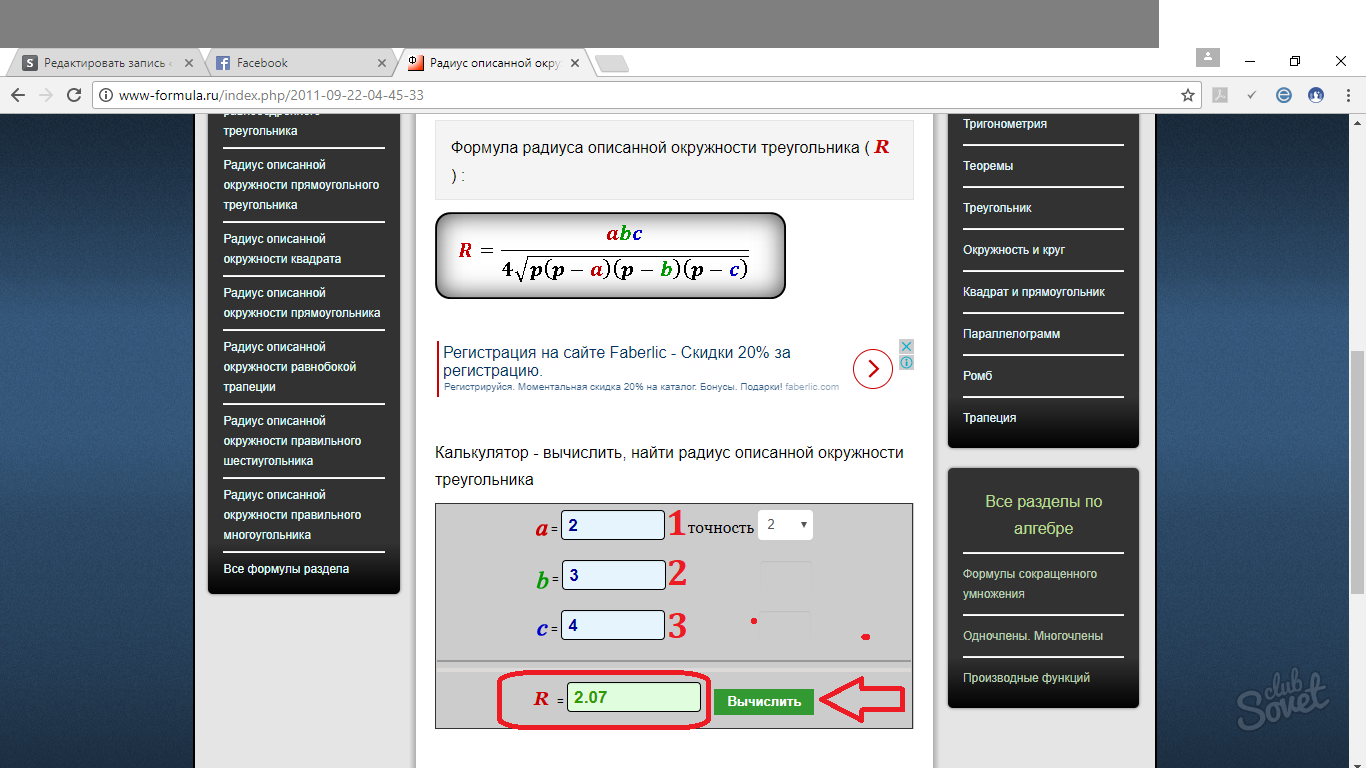
الموارد عبر الإنترنت لحساب نصف قطر الدائرة
من السهل جدًا الخلط بين كل هذه الصيغ. لذلك ، إذا لزم الأمر ، يمكنك استخدام حاسبات على الإنترنت، مما سيساعدك في حل المشكلات المتعلقة بإيجاد نصف القطر. مبدأ تشغيل هذه البرامج الصغيرة بسيط للغاية. استبدل قيمة الضلع في الحقل المناسب واحصل على إجابة جاهزة. يمكنك اختيار عدة خيارات لتقريب الإجابة: إلى الكسور العشرية ، والمئات ، والألف ، إلخ.