Durchmesser des umschriebenen Kreises eines Dreiecks. Zusammenfassung der Lektion „umschriebener Kreis“. So ermitteln Sie den Radius eines um ein Dreieck umschriebenen Kreises – die allgemeine Formel
In diesem Teil besprechen wir den umschriebenen Kreis (oft „in der Nähe“) eines Dreiecks. Lassen Sie uns zunächst eine Definition geben.
1. Existenz und Mittelpunkt des umschriebenen Kreises
Hier stellt sich die Frage: Gibt es einen solchen Kreis für jedes Dreieck? Es stellt sich heraus, dass ja, für alle. Und darüber hinaus formulieren wir nun einen Satz, der auch die Frage beantwortet, wo der Mittelpunkt des umschriebenen Kreises liegt.
Formeln zum Ermitteln der Länge der Diagonale eines Rechtecks
Formel auf der Seite eines Rechtecks mit Durchmesser und Winkel β. Sie wird als Diagonale eines Rechtecks für jedes Segment bezeichnet, das zwei Eckpunkte gegenüberliegender Ecken des Rechtecks verbindet. Die Formel für die Diagonale eines Rechtecks in Bezug auf die beiden Seiten des Rechtecks.
Die Formel für die Diagonale eines Rechtecks in der Fläche und auf beiden Seiten. Die Formel für die Diagonale eines Rechtecks entlang des Umfangs und auf beiden Seiten. Die Formel für die Diagonale eines Rechtecks in Bezug auf den Radius des umschriebenen Kreises. Die Formel für die Diagonale eines Rechtecks entlang des Umfangs eines Kreises.
Sieht aus wie das:
Nehmen wir den Mut zusammen und beweisen wir diesen Satz. Wenn Sie das Thema „“ bereits gelesen haben und herausgefunden haben, warum sich die drei Winkelhalbierenden in einem Punkt schneiden, wird es für Sie einfacher, aber wenn Sie es noch nicht gelesen haben, machen Sie sich keine Sorgen: Jetzt werden wir alles herausfinden aus.
Den Beweis führen wir mit dem Konzept des Ortspunktes (LPT) durch.
Die Formel für die Diagonale eines Rechtecks als Sinus des an die Diagonale angrenzenden Winkels und der Länge der diesem Winkel gegenüberliegenden Seite. Die Formel für die Diagonale eines Rechtecks als Kosinus des an die Diagonale angrenzenden Winkels und der Länge der an diesen Winkel angrenzenden Seite. Die Formel für die Diagonale eines Rechtecks als Sinus des spitzen Winkels zwischen den Diagonalen und der Fläche des Rechtecks.
Formeln zur Bestimmung der Länge des Umfangs eines Rechtecks
Der Umfang eines Rechtecks wird als Summe der Längen aller Seiten des Rechtecks bezeichnet. Die Formel für den Umfang eines Rechtecks in Bezug auf die beiden Seiten des Rechtecks. Die Formel für den Umfang eines Rechtecks mit gegebener Fläche und beiden Seiten. Die Formel für den Umfang eines Rechtecks entlang der Diagonale und auf beiden Seiten.
Ist die Kugelmenge zum Beispiel ein „geometrischer Ort“ runder Objekte? Nein, natürlich, denn es gibt runde ... Wassermelonen. Aber ist eine Gruppe von Menschen, ein „geometrischer Ort“, in der Lage zu sprechen? Weder noch, denn es gibt Babys, die nicht sprechen können. Im Leben ist es generell schwierig, ein Beispiel für einen echten „geometrischen Ort der Punkte“ zu finden. Geometrie ist einfacher. Hier ist zum Beispiel genau das, was wir brauchen:
Die Formel für den Umfang eines Rechtecks, ausgedrückt als Radius des umschriebenen Kreises und auf beiden Seiten. Die Formel für den Umfang eines Rechtecks, gegeben durch den Durchmesser des umschriebenen Kreises und beider Seiten. Sie wird als Fläche des Rechtecks in dem von den Seiten des Rechtecks begrenzten Raum bezeichnet, also innerhalb der Umfangsfläche des Rechtecks.
Formeln zur Bestimmung der Fläche eines Rechtecks
Formel für die Fläche eines Rechtecks mit zwei Seiten. Die Formel für die Fläche eines Rechtecks entlang des Umfangs und auf beiden Seiten. Die Formel für die Fläche eines Rechtecks entlang der Diagonale und auf beiden Seiten. Die Formel für die Fläche eines Rechtecks entlang der Diagonale und den Sinus des spitzen Winkels zwischen den Diagonalen.
Hier ist die Menge die Mittelsenkrechte, und die Eigenschaft „“ besteht darin, „den gleichen Abstand (Punkt) von den Enden des Segments zu haben“.
Lass uns das Prüfen? Sie müssen also zwei Dinge sicherstellen:
Verbinde mit und mit. Dann ist die Linie der Median und die Höhe in. Also, - gleichschenklig, - wir haben sichergestellt, dass jeder Punkt, der auf der Mittelsenkrechten liegt, gleich weit von den Punkten und entfernt ist.
Kreis, der um ein Rechteck begrenzt ist
Die Formel für die Fläche eines Rechtecks, wenn der Radius des umschriebenen Kreises und eine beliebige Seite gegeben sind. Die Formel für die Fläche eines Rechtecks in einem Kreis ist ein Kreis eines Kreises und auf beiden Seiten. Man spricht von einem um ein Rechteck begrenzten Kreis, einem Kreis, der durch die vier Eckpunkte des Rechtecks verläuft und dessen Mittelpunkt der Schnittpunkt der Diagonalen des Rechtecks ist.
Formeln zum Ermitteln des Radius eines um ein Rechteck umschriebenen Kreises
Die Formel für den Radius eines Kreises, der von einem Rechteck durch zwei Seiten begrenzt wird. Die Formel für den Radius eines Kreises, der entlang des Umfangs des Quadrats und auf beiden Seiten um ein Rechteck herum beschrieben wird. Die Formel für den Radius eines Kreises, der um ein Rechteck herum beschrieben wird, ausgedrückt durch die Fläche des Rechtecks und die Länge einer seiner Seiten.
Nehmen Sie die Mitte und verbinden Sie und. Habe den Median erhalten. Aber - je nach Bedingung gleichschenklig, nicht nur der Median, sondern auch die Höhe, also die Mediansenkrechte. Das bedeutet, dass der Punkt genau auf der Mittelsenkrechten liegt.
Alle! Wir haben die Tatsache vollständig bestätigt, dass die Mittelsenkrechte zu einem Segment der Ort der Punkte ist, die von den Enden des Segments gleich weit entfernt sind.
Die Formel für den Radius eines Kreises, der um ein Rechteck entlang der Diagonale des Rechtecks umschrieben wird. Die Formel für den Radius eines Kreises, der um ein Rechteck herum durch den Umfangsdurchmesser des Kreises beschrieben wird. Die Formel für den Radius eines Kreises um ein Rechteck wird anhand des Sinus des an die Diagonale angrenzenden Winkels und der Länge der diesem Winkel gegenüberliegenden Seite beschrieben.
Der Kreis, der das gegebene Polygon umgibt, ist der umschriebene Kreis. Die meisten Menschen haben die Begriffe Umfang und Radius gehört, aber der Begriff „begrenzter Kreis“ ist weniger geläufig. Stellen Sie sich ein zweidimensionales Polygon mit geraden Seiten vor, wie ein Dreieck. Stellen Sie sich einen Kreis um ein Dreieck vor, so dass es alle drei Eckpunkte berührt; Es ist ein begrenzter Kreis. Um Ihren Radius zu berechnen, verwenden Sie einfach eine einfache Algebra und einen Taschenrechner.
Das ist alles schön und gut, aber haben wir den eingegrenzten Kreis vergessen? Überhaupt nicht, wir haben uns nur einen „Brückenkopf für den Angriff“ vorbereitet.
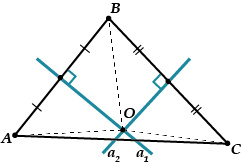
Betrachten Sie ein Dreieck. Zeichnen wir zwei mittlere Senkrechte und, sagen wir, zu den Segmenten und. Sie werden sich irgendwann kreuzen, den wir benennen werden.
Überprüfen Sie alle Ihre Messungen und stellen Sie sicher, dass der Kompass anzeigt, dass er sich beim Kreisen nicht ändert.
- Es ist äußerst wichtig, genau und genau zu messen.
- Nicht alle Polygone können einen begrenzten Kreis haben.
Somit ist die Fläche eines in ein Sechseck eingeschriebenen Kreises gleich. Nun wenden wir uns dem beschrifteten Quadrat zu. Da die Diagonale des Quadrats gleich der Seite der Wurzelzeiten ist, gilt. Dann hat der Radius eines in ein Quadrat eingeschriebenen Kreises die halbe Seitenlänge. Sie werden also sehen, dass der Radius eines in ein Dreieck eingeschriebenen Kreises halb so groß ist wie der Radius eines in ein Dreieck umschriebenen Kreises, da der Umfang eines Kreises durch ein geteiltes Medium in zwei Teile proportional zu 1 und dann dem Radius beschrieben wird des eingeschriebenen Kreises wird sein.
Und nun, Achtung!
Der Punkt liegt auf der Mittelsenkrechten;
der Punkt liegt auf der Mittelsenkrechten.
Und das bedeutet und.
Daraus ergeben sich mehrere Dinge:
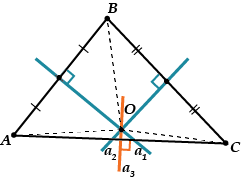
Erstens, der Punkt muss auf der dritten Mittelsenkrechten zum Segment liegen.
Kreismessung und -näherung
Somit beträgt die Fläche des eingeschriebenen Kreises. Und das Problem besteht darin, zu beweisen, dass die Summe dieser Flächen gleich der Fläche des inneren Kreises ist. Berechnen wir also die Summe der Flächen der Kronen. Dies ist die Summe der Flächen der Kronen. Sie können sehen, dass wir 3 Strahlenkreise haben. In diesem Artikel wird eine Hypothese vorgeschlagen, ein Vorwand für die Betrachtung einiger Punkte der Mathematik dieser Zeit in Mesopotamien.
Indem er zwischen zwei Sechsecken einen Kreis bildet, dessen Umfang leicht berechnet werden kann, und dann die Anzahl der Seiten sukzessive verdoppelt, erhält er einen Rahmen aus Polygonen mit 96 Seiten. Es ist wahrscheinlich einfacher, die Leistung durch die Angabe numerischer Werte zu bewerten.
Das heißt, die Mittelsenkrechte muss ebenfalls durch den Punkt gehen und alle drei Mittelsenkrechten schneiden sich in einem Punkt.
Zweitens: Wenn wir einen Kreis mit einem Mittelpunkt in einem Punkt und einem Radius zeichnen, dann wird dieser Kreis auch durch den Punkt und durch den Punkt gehen, das heißt, es wird der umschriebene Kreis sein. Dies bedeutet, dass es bereits existiert, dass der Schnittpunkt der drei Mittelsenkrechten der Mittelpunkt des umschriebenen Kreises für jedes Dreieck ist.
Wir sehen hier das Interesse und die Wirksamkeit von Beobachtungsmethoden: Einerseits liefern sie eine Annäherung, andererseits ermöglichen sie die Kontrolle eines perfekten Fehlers. Soweit ich weiß, ist Archimedes der erste, der seine Ergebnisse bezüglich des Kreises explizit begründet und Schritt für Schritt eine Reihe von Argumenten anführt, die erklären, warum seine Behauptungen wahr sind. Aber er ist nicht der Erste, der sich für den Kreis und sein Maß interessiert. Wir haben sehr alte Beweise, einen in Ägypten und einige andere in Mesopotamien, die in diese Richtung gehen.
Und es gibt einige „babylonische“ Tontafeln aus derselben Zeit und entlang des Umfangs oder Bereichs der Scheibe. Dies ist das Thema dieses Artikels. Die Wanderung kann beginnen, jedoch vor der Abreise nach Babylon im 17. oder 18. Jahrhundert v. Chr. Es wurde eine babylonische Tontafel gefunden, die das Verhältnis des Umfangs eines Sechsecks zum Umfang seines umschriebenen Kreises angibt.
Und das Letzte: über Einzigartigkeit. Es ist (fast) klar, dass der Punkt auf einzigartige Weise gewonnen werden kann und daher auch der Kreis einzigartig ist. Na ja, „fast“ – das überlassen wir Ihnen. Hier haben wir den Satz bewiesen. Sie können „Hurra!“ rufen.
Und wenn das Problem die Frage ist: „Finden Sie den Radius des umschriebenen Kreises“? Oder umgekehrt, der Radius ist vorgegeben, Sie müssen aber etwas anderes finden? Gibt es eine Formel, die den Radius des umschriebenen Kreises mit den anderen Elementen eines Dreiecks in Beziehung setzt?
Und sie werden oft in der einen oder anderen Form hinzugefügt. Dies war die zweite Frage, die mich vor ein Problem stellte: Konnten die Babylonier diesen Wert wirklich experimentell ermitteln? Derzeit ist das Erlebnis einfach zu bedienen, mit einem Schneidermesser und Alltagsgegenständen unterschiedlicher Durchmesser: Bratpfanne, Kochtopf, Blechdosen. Umfang und Durchmesser werden gemessen und die Teilung vorgenommen. Die Unterschiede lagen bei der dritten Dezimalstelle. Natürlich gibt es keine derart präzisen Industrieartikel und auch keine in Millimetern eingeteilten Nähermeter.
Für die Messung ist es dünner: Seil, Lederband, kann sich unter Spannung dehnen und problemlos zusammenziehen. Andererseits dehnt sich getrocknete Papyrusrinde nicht. Leider hatte ich es nicht. Offensichtlich sind sie nicht abgestuft, aber das ist nicht ernst: Uns interessiert das Verhältnis zweier Längen: vom Umfang und Durchmesser und nicht von den Längen selbst. Es ist einfach, mit Rattan um einen Gegenstand herumzugehen und ihn zu schneiden. Merkwürdigerweise ist es weniger einfach, Rattanfäden genau auf den Durchmesser zuzuschneiden. Tatsächlich ist die Oberkante der Keramik häufig abgerundet.
Sehr oft müssen Sie beim Lösen geometrischer Probleme Aktionen mit Hilfsfiguren ausführen. Ermitteln Sie beispielsweise den Radius eines eingeschriebenen oder umschriebenen Kreises usw. In diesem Artikel erfahren Sie, wie Sie den Radius eines Kreises ermitteln, der ein Dreieck umschreibt. Oder mit anderen Worten, der Radius des Kreises, in den das Dreieck eingeschrieben ist.
Daher ist es notwendig, das Rattan um den Umfang herum zu befestigen und dann das zweite Rattanmesser entsprechend dem Innendurchmesser des ersten zu schneiden. Es bleibt das Verhältnis der beiden Längen zu berechnen, ohne sie zu kennen genaue Werte, was erreicht werden kann, indem man zum eigentlichen Ursprung der Teilung zurückkehrt. 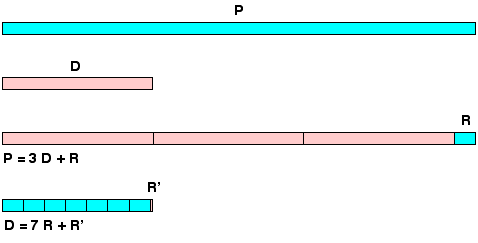
Meine beste Leistung war 6, 8 Mal, also 6 Mal, mit einer wunderbaren Pause. Diese Experimente überzeugten mich jedoch davon, dass die Babylonier keinen experimentellen Wert hatten, zumindest nicht von dieser Route. Aber in diesem Fall stellen sich zwei Fragen.
So ermitteln Sie den Radius eines um ein Dreieck umschriebenen Kreises – die allgemeine Formel
Die allgemeine Formel lautet wie folgt: R = abc/4√p(p - a)(p - b)(p - c), wobei R der Radius des umschriebenen Kreises und p der Umfang des Dreiecks geteilt durch 2 ist (halber Umfang). a, b, c sind die Seiten des Dreiecks.
Finden Sie den Radius des Umkreises des Dreiecks, wenn a = 3, b = 6, c = 7.
Frage 1: Wenn es nicht experimentell ist, ist es theoretisch, geometrisch. 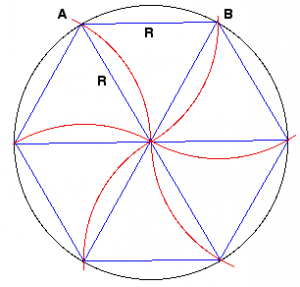
Somit ist der Umfang P eines Kreises größer als der eines Sechsecks und das Verhältnis zwischen ihnen ist gleich. Für uns ist es ganz natürlich, den Umfang eines Kreises abzuschätzen, der im Verhältnis zu dem, was das Sechseck selbst kennt, unbekannt ist.
Später werden wir sehen, was wir davon halten. Hypothese 1: Die Babylonier kannten den Satz des Pythagoras tausend Jahre zuvor. Hypothese 2: Sie wussten, dass sie Rechtecke mit ganzzahligen Seiten gefunden hatten. Vielleicht nicht alle, aber zumindest diejenigen, deren Hypotenuse und eine der Seiten ganze Zahlen sind.
Basierend auf der obigen Formel berechnen wir also den Halbumfang:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Ersetzen Sie die Werte in der Formel und erhalten Sie:
R = 3 x 6 x 7/4√8(8 - 3)(8 - 6)(8 - 7) = 126/4√(8 x 5 x 2 x 1) = 126/4√80 = 126/16 √5.
Antwort: R = 126/16√5
So ermitteln Sie den Radius eines Kreises, der von einem gleichseitigen Dreieck umschrieben wird
Um den Radius eines um ein gleichseitiges Dreieck umschriebenen Kreises zu ermitteln, gibt es eine ziemlich einfache Formel: R = a/√3, wobei a die Größe seiner Seite ist.
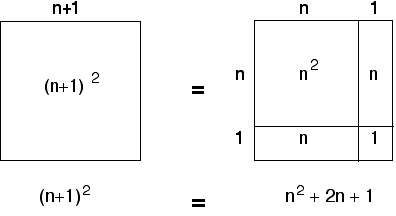
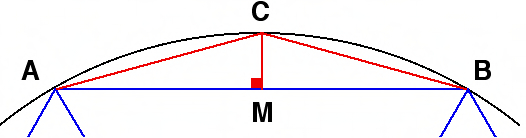
Natürlich gibt es keinen Beweis dafür, dass die Babylonier dies taten. Dies kann nur durch die Entdeckung einer neuen Tontafel erreicht werden. Darüber hinaus basiert diese Idee auf Hypothese 1: Wussten die Babylonier wirklich, wie man solche Dreiecke findet? 
Die letzten 15 Zeilen sind in 4 Spalten unterteilt, wobei die ersten beiden Zeilen den Inhalt definieren. Spalte 4 enthält das Vorzeichen gefolgt von den Zahlen von 1 bis.
Beispiel: Die Seite eines gleichseitigen Dreiecks ist 5. Ermitteln Sie den Radius des umschriebenen Kreises.
Da alle Seiten eines gleichseitigen Dreiecks gleich sind, müssen Sie zur Lösung des Problems lediglich seinen Wert in die Formel eingeben. Wir erhalten: R = 5/√3.
Antwort: R = 5/√3.
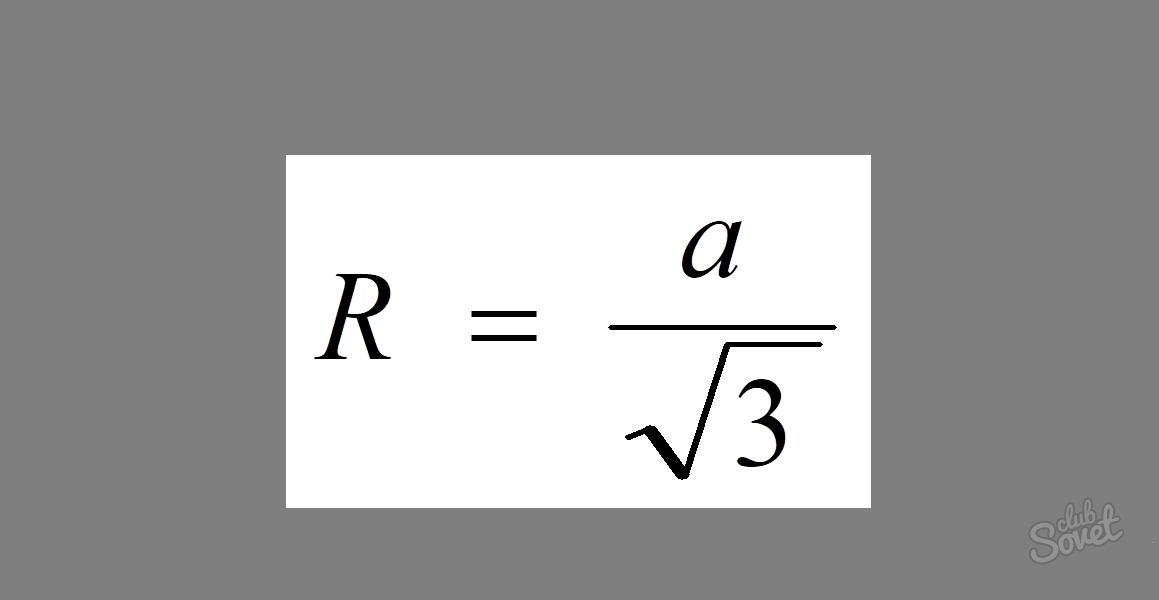
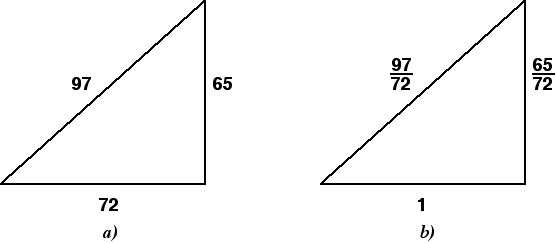
So ermitteln Sie den Radius eines um ein rechtwinkliges Dreieck umschriebenen Kreises
Die Formel sieht so aus: R = 1/2 × √(a² + b²) = c/2, wobei a und b die Schenkel und c die Hypotenuse sind. Wenn wir die Quadrate der Schenkel eines rechtwinkligen Dreiecks addieren, erhalten wir das Quadrat der Hypotenuse. Wie aus der Formel hervorgeht, liegt dieser Ausdruck unter der Wurzel. Indem wir die Wurzel des Quadrats der Hypotenuse berechnen, erhalten wir die Länge selbst. Die Multiplikation des resultierenden Ausdrucks mit 1/2 führt schließlich zum Ausdruck 1/2 × c = c/2.
Die Spalten 1, 2 und 3 beziehen sich auf rechtwinklige Dreiecke. Die Spalten 2 und 3 geben jeweils die kleinste Seite und Hypotenuse jedes Dreiecks an. Spalte 1 gibt das Quadrat des Verhältnisses auf beiden Seiten der rechten Ecke an. Zeile 5 beginnt beispielsweise im Sexualsystem.
Das ist zu präzise, um wahr zu sein, aber Sie können überprüfen, ob es auch für andere Zeichenfolgen gilt. Es gibt Kontroversen über die Methoden, die die Babylonier möglicherweise zur Zusammenstellung dieser Tabelle verwendet haben. Es gibt auch Fehler in der Kopie des Schreibers und kleine Rätsel, wie zum Beispiel Zeile 11, die als Seiten 45 und 1 15 angibt, also in der Dezimalzahl: 45, und beide sind Vielfache von 15, und dieses Dreieck ist nichts als ein Dreieck von Seiten. Warum wird es nicht in dieser viel einfacheren Form angegeben? Und welchen Vorteil könnte es haben, das Quadrat der Steigung anstelle der Steigung selbst anzugeben?
Beispiel: Berechnen Sie den Radius des umschriebenen Kreises, wenn die Schenkel des Dreiecks 3 und 4 sind. Setzen Sie die Werte in die Formel ein. Wir erhalten: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2,5.
In diesem Ausdruck ist 5 die Länge der Hypotenuse.
Antwort: R = 2,5.
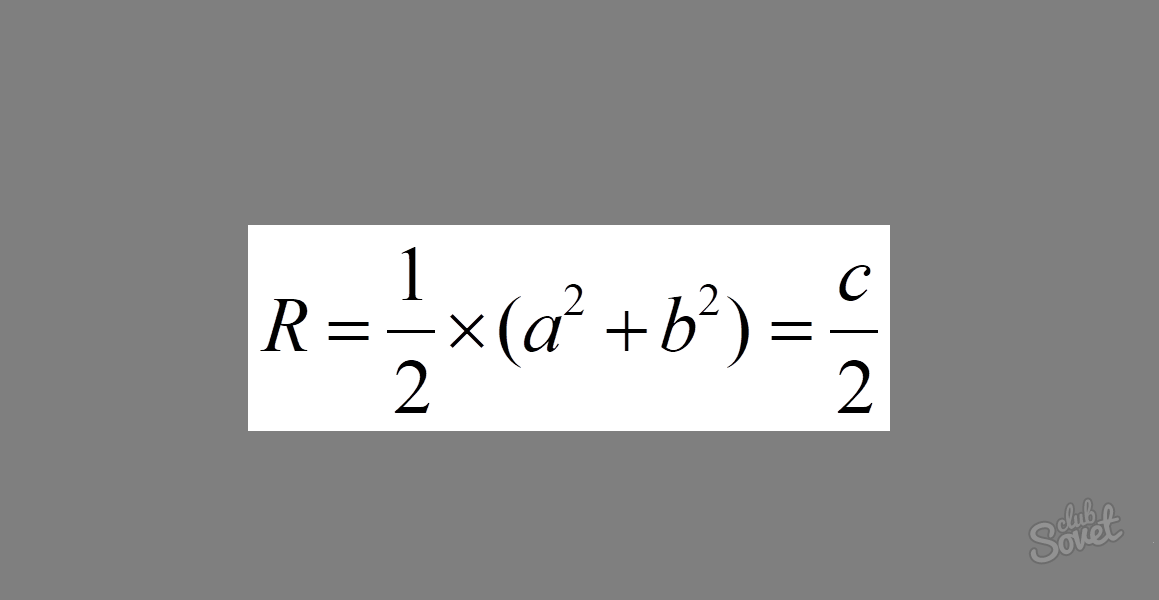
So ermitteln Sie den Radius eines Kreises, der um ein gleichschenkliges Dreieck beschrieben wird
Die Formel sieht so aus: R = a² / √ (4a² - b²), wobei a die Länge des Schenkels des Dreiecks und b die Länge der Basis ist.
Beispiel: Berechnen Sie den Radius eines Kreises, wenn seine Hüfte = 7 und seine Basis = 8 ist.
Lösung: Wir setzen diese Werte in die Formel ein und erhalten: R \u003d 7² / √ (4 × 7² - 8²).
R = 49/√(196 - 64) = 49/√132. Die Antwort kann direkt so geschrieben werden.
Antwort: R = 49/√132
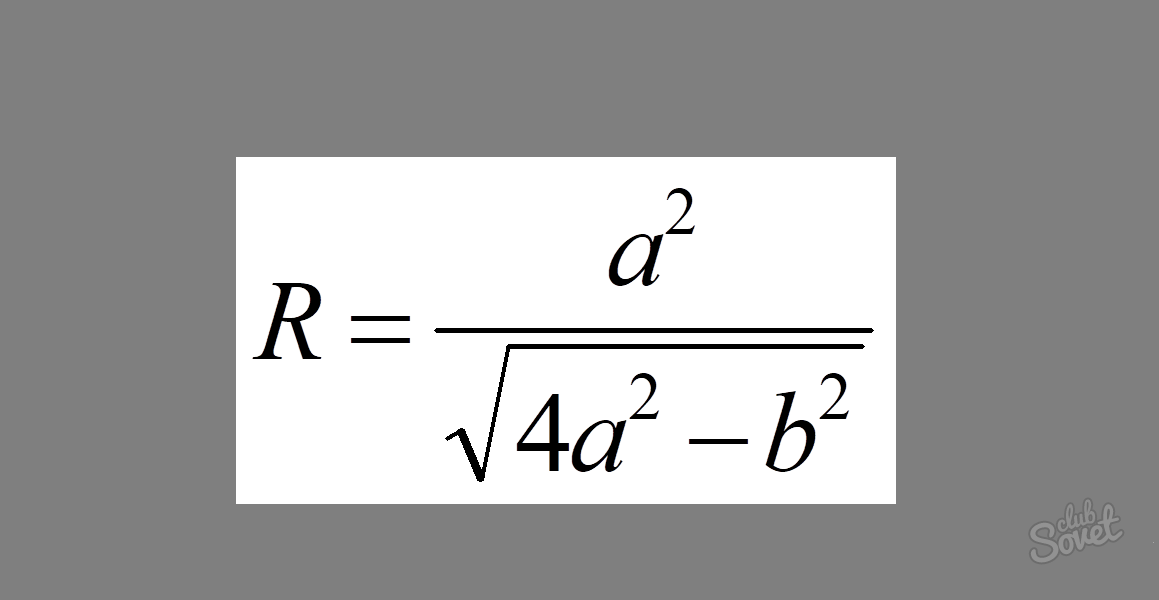
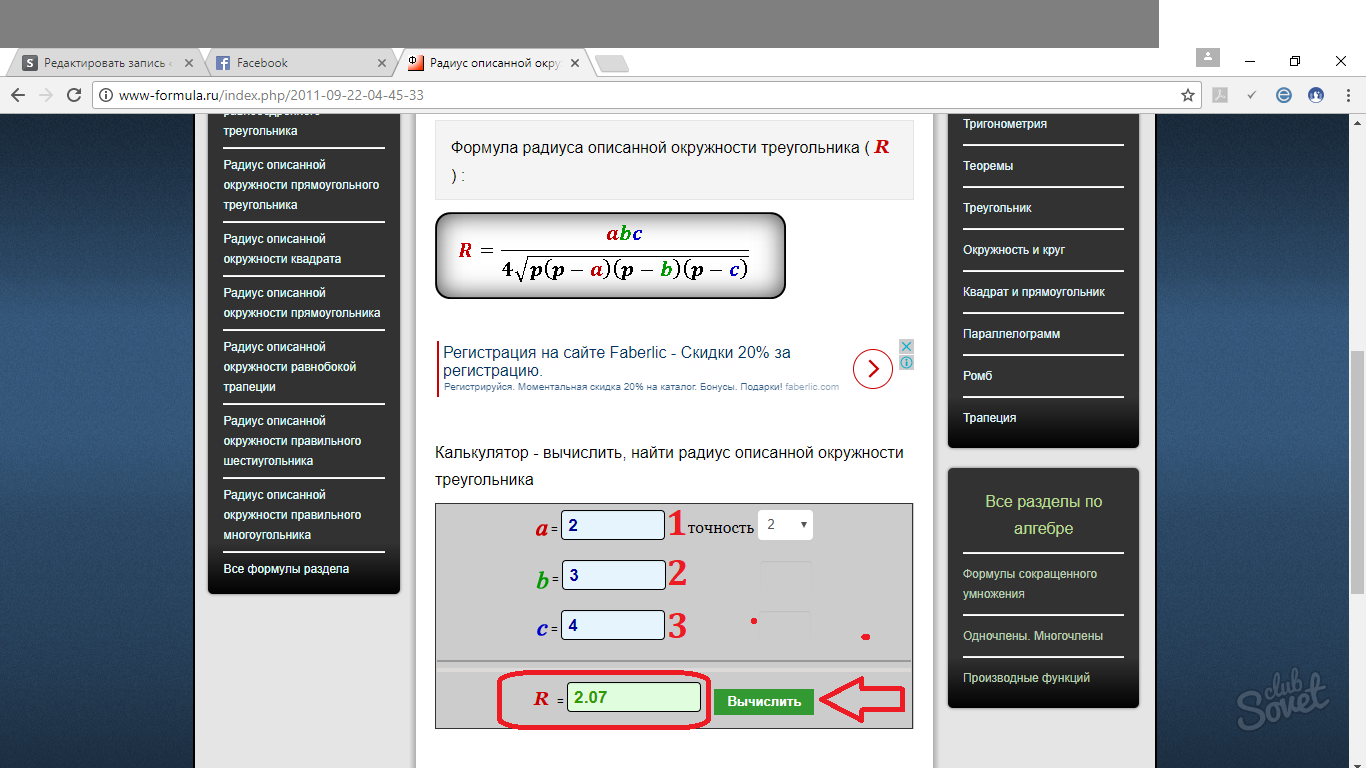
Online-Ressourcen zur Berechnung des Radius eines Kreises
Bei all diesen Formeln kommt man sehr leicht durcheinander. Daher können Sie bei Bedarf verwenden Online-Rechner, das Ihnen bei der Lösung von Problemen beim Finden des Radius hilft. Das Funktionsprinzip solcher Miniprogramme ist sehr einfach. Geben Sie den Wert der Seite in das entsprechende Feld ein und Sie erhalten eine vorgefertigte Antwort. Sie können zwischen mehreren Optionen zum Runden der Antwort wählen: auf Dezimalstellen, Hundertstel, Tausendstel usw.