Διάμετρος του περιγεγραμμένου κύκλου ενός τριγώνου. Περίληψη του μαθήματος «περιγεγραμμένος κύκλος». Πώς να βρείτε την ακτίνα ενός κύκλου που περιβάλλεται γύρω από ένα τρίγωνο - ο γενικός τύπος
Σε αυτό το μέρος, θα συζητήσουμε τον περιγεγραμμένο κύκλο γύρω από ένα τρίγωνο (που συχνά λέγεται "κοντά"). Πρώτα απ 'όλα, ας δώσουμε έναν ορισμό.
1. Ύπαρξη και κέντρο του περιγεγραμμένου κύκλου
Εδώ τίθεται το ερώτημα: υπάρχει τέτοιος κύκλος για οποιοδήποτε τρίγωνο; Αποδεικνύεται ότι ναι, για όλους. Και επιπλέον, θα διατυπώσουμε τώρα ένα θεώρημα που απαντά επίσης στο ερώτημα, πού είναι το κέντρο του περιγεγραμμένου κύκλου.
Τύποι για την εύρεση του μήκους της διαγωνίου ενός ορθογωνίου
Τύπος στην πλευρά ενός ορθογωνίου σε διάμετρο και γωνία β. Ονομάζεται διαγώνιος ορθογωνίου για κάθε τμήμα που συνδέει δύο κορυφές απέναντι γωνίες του ορθογωνίου. Ο τύπος για τη διαγώνιο ενός παραλληλογράμμου ως προς τις δύο πλευρές του ορθογωνίου.
Ο τύπος για τη διαγώνιο ενός ορθογωνίου στο εμβαδόν και στις δύο πλευρές. Ο τύπος για τη διαγώνιο ενός ορθογωνίου κατά μήκος της περιμέτρου και στις δύο πλευρές. Ο τύπος για τη διαγώνιο ενός ορθογωνίου ως προς την ακτίνα του περιγεγραμμένου κύκλου. Ο τύπος για τη διαγώνιο ενός ορθογωνίου κατά μήκος της περιφέρειας ενός κύκλου.
Μοιάζει με αυτό:
Ας συγκεντρώσουμε το θάρρος και ας αποδείξουμε αυτό το θεώρημα. Εάν έχετε ήδη διαβάσει το θέμα "", έχετε καταλάβει γιατί οι τρεις διχοτόμοι τέμνονται σε ένα σημείο, τότε θα είναι πιο εύκολο για εσάς, αλλά αν δεν το έχετε διαβάσει, μην ανησυχείτε: τώρα θα τα καταλάβουμε όλα έξω.
Θα πραγματοποιήσουμε την απόδειξη χρησιμοποιώντας την έννοια του τόπου των σημείων (LPT).
Ο τύπος για τη διαγώνιο ενός ορθογωνίου ως προς το ημίτονο της γωνίας δίπλα στη διαγώνιο και το μήκος της πλευράς απέναντι από αυτήν τη γωνία. Ο τύπος για τη διαγώνιο ενός ορθογωνίου ως προς το συνημίτονο της γωνίας που γειτνιάζει με τη διαγώνιο και το μήκος της πλευράς που γειτνιάζει με τη γωνία αυτή. Ο τύπος για τη διαγώνιο ενός ορθογωνίου ως προς το ημίτονο της οξείας γωνίας μεταξύ των διαγωνίων και του εμβαδού του ορθογωνίου.
Τύποι για τον προσδιορισμό του μήκους της περιμέτρου ενός ορθογωνίου
Η περίμετρος ενός παραλληλογράμμου ονομάζεται το άθροισμα των μηκών όλων των πλευρών του ορθογωνίου. Ο τύπος για την περίμετρο ενός παραλληλογράμμου ως προς τις δύο πλευρές του ορθογωνίου. Ο τύπος για την περίμετρο ενός ορθογωνίου δεδομένου του εμβαδού και των δύο πλευρών. Ο τύπος για την περίμετρο ενός ορθογωνίου κατά μήκος της διαγώνιας και στις δύο πλευρές.
Λοιπόν, για παράδειγμα, το σύνολο των μπάλων είναι ένα «γεωμετρικό μέρος» στρογγυλών αντικειμένων; Όχι, φυσικά, γιατί υπάρχουν στρογγυλά... καρπούζια. Είναι όμως ένα σύνολο ανθρώπων, ένας «γεωμετρικός τόπος», ικανός να μιλήσει; Ούτε, γιατί υπάρχουν μωρά που δεν μπορούν να μιλήσουν. Στη ζωή, είναι γενικά δύσκολο να βρεθεί ένα παράδειγμα ενός πραγματικού «γεωμετρικού τόπου σημείων». Η γεωμετρία είναι πιο εύκολη. Εδώ, για παράδειγμα, είναι ακριβώς αυτό που χρειαζόμαστε:
Ο τύπος για την περίμετρο ενός ορθογωνίου ως προς την ακτίνα του περιγεγραμμένου κύκλου και στις δύο πλευρές. Ο τύπος για την περίμετρο ενός ορθογωνίου δίνεται η διάμετρος του περιγεγραμμένου κύκλου και των δύο πλευρών. Ονομάζεται το εμβαδόν του ορθογωνίου στον χώρο που οριοθετείται από τις πλευρές του ορθογωνίου, δηλαδή μέσα στην περιμετρική περιοχή του ορθογωνίου.
Τύποι για τον προσδιορισμό του εμβαδού ενός ορθογωνίου
Τύπος για το εμβαδόν ενός ορθογωνίου με δύο πλευρές. Ο τύπος για το εμβαδόν ενός ορθογωνίου κατά μήκος της περιμέτρου και στις δύο πλευρές. Ο τύπος για το εμβαδόν ενός ορθογωνίου κατά μήκος της διαγώνιας και στις δύο πλευρές. Ο τύπος για το εμβαδόν ενός ορθογωνίου κατά μήκος της διαγωνίου και του ημιτόνου της οξείας γωνίας μεταξύ των διαγωνίων.
Εδώ το σύνολο είναι η μέση κάθετος και η ιδιότητα "" είναι "να είναι ίση απόσταση (σημείο) από τα άκρα του τμήματος."
Ας ελέγξουμε? Επομένως, πρέπει να βεβαιωθείτε για δύο πράγματα:
Συνδέστε με και με. Τότε η γραμμή είναι η διάμεσος και το ύψος μέσα. Άρα, - ισοσκελές, - φροντίσαμε ότι οποιοδήποτε σημείο βρίσκεται στην κάθετη διχοτόμο είναι εξίσου μακριά από τα σημεία και.
Κύκλος οριοθετημένος γύρω από ένα ορθογώνιο
Ο τύπος για το εμβαδόν ενός ορθογωνίου δεδομένης της ακτίνας του περιγεγραμμένου κύκλου και οποιασδήποτε πλευράς. Ο τύπος για το εμβαδόν ενός ορθογωνίου σε κύκλο είναι κύκλος κύκλου και στις δύο πλευρές. Ονομάζεται κύκλος οριοθετημένος γύρω από ένα ορθογώνιο, σε κύκλο που διέρχεται από τις τέσσερις κορυφές του ορθογωνίου, το κέντρο του οποίου είναι η τομή των διαγωνίων του παραλληλογράμμου.
Τύποι για την εύρεση της ακτίνας ενός κύκλου που περιβάλλεται γύρω από ένα ορθογώνιο
Ο τύπος για την ακτίνα ενός κύκλου που οριοθετείται από ένα ορθογώνιο από δύο πλευρές. Ο τύπος για την ακτίνα ενός κύκλου που περιβάλλεται γύρω από ένα ορθογώνιο κατά μήκος της περιμέτρου του τετραγώνου και σε κάθε πλευρά. Ο τύπος για την ακτίνα ενός κύκλου περιγράφεται γύρω από ένα ορθογώνιο ως προς το εμβαδόν του ορθογωνίου και το μήκος μιας από τις πλευρές του.
Πάρτε - τη μέση και συνδέστε και. Πήρε τη διάμεσο. Αλλά - ισοσκελές κατά συνθήκη, όχι μόνο η διάμεσος, αλλά και το ύψος, δηλαδή η διάμεσος κάθετος. Αυτό σημαίνει ότι το σημείο βρίσκεται ακριβώς στην κάθετη διχοτόμο.
Ολα! Επαληθεύσαμε πλήρως το γεγονός ότι η κάθετη διχοτόμος σε ένα τμήμα είναι ο τόπος των σημείων που απέχουν ίσα από τα άκρα του τμήματος.
Ο τύπος για την ακτίνα ενός κύκλου που περιβάλλεται γύρω από ένα ορθογώνιο κατά μήκος της διαγώνιας του ορθογωνίου. Ο τύπος για την ακτίνα ενός κύκλου που περιγράφεται γύρω από ένα ορθογώνιο από την περιφερειακή διάμετρο του κύκλου. Ο τύπος για την ακτίνα ενός κύκλου που περιγράφεται γύρω από ένα ορθογώνιο ως προς το ημίτονο της γωνίας δίπλα στη διαγώνιο και το μήκος της πλευράς απέναντι από αυτή τη γωνία.
Ο κύκλος που περιβάλλει το δεδομένο πολύγωνο είναι ο περιγεγραμμένος κύκλος. Οι περισσότεροι άνθρωποι έχουν ακούσει τους όρους περιφέρεια και ακτίνα, αλλά ο περιορισμένος κύκλος είναι ένας λιγότερο γνωστός όρος. Φανταστείτε ένα δισδιάστατο πολύγωνο με ευθείες πλευρές, σαν τρίγωνο. Φανταστείτε έναν κύκλο γύρω από ένα τρίγωνο έτσι ώστε να αγγίζει και τις τρεις κορυφές του. είναι ένας περιορισμένος κύκλος. Για να υπολογίσετε την ακτίνα σας, απλώς χρησιμοποιήστε μια απλή άλγεβρα και μια αριθμομηχανή.
Ωραία όλα αυτά, αλλά έχουμε ξεχάσει τον περιγεγραμμένο κύκλο; Καθόλου, απλώς ετοιμάσαμε «προγεφύρωμα για την επίθεση».
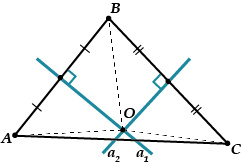
Θεωρήστε ένα τρίγωνο. Ας σχεδιάσουμε δύο διαμέσους κάθετους και, ας πούμε, στα τμήματα και. Θα διασταυρωθούν κάποια στιγμή, που θα ονομάσουμε.
Ελέγξτε όλες τις μετρήσεις σας και βεβαιωθείτε ότι η πυξίδα λέει ότι δεν αλλάζει ενώ κάνετε κύκλους.
- Είναι εξαιρετικά σημαντικό να μετράτε με ακρίβεια και ακρίβεια.
- Δεν μπορούν όλα τα πολύγωνα να έχουν περιορισμένο κύκλο.
Έτσι, το εμβαδόν ενός κύκλου που εγγράφεται σε ένα εξάγωνο είναι ίσο με. Τώρα στραφούμε στο εγγεγραμμένο τετράγωνο. Εφόσον η διαγώνιος του τετραγώνου είναι ίση με την πλευρά των χρόνων της ρίζας, έχουμε. Τότε η ακτίνα ενός κύκλου εγγεγραμμένου σε ένα τετράγωνο θα έχει το μισό μέτρο της πλευράς. Έτσι, θα δείτε ότι η ακτίνα ενός κύκλου που είναι εγγεγραμμένος σε ένα τρίγωνο είναι η μισή της ακτίνας ενός κύκλου που περιγράφεται σε ένα τρίγωνο, αφού η περιφέρεια ενός κύκλου περιγράφεται από ένα διαιρεμένο μέσο σε δύο μέρη ανάλογα με το 1, και μετά η ακτίνα του εγγεγραμμένου κύκλου θα είναι.
Και τώρα, προσοχή!
Το σημείο βρίσκεται στην κάθετη διχοτόμο.
το σημείο βρίσκεται στην κάθετη διχοτόμο.
Και αυτό σημαίνει και.
Από αυτό προκύπτουν αρκετά πράγματα:
Πρώτα, το σημείο πρέπει να βρίσκεται στην τρίτη κάθετη διχοτόμο, στο τμήμα.
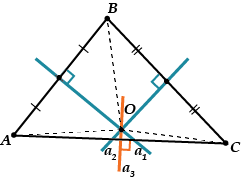
Μέτρηση και προσέγγιση κύκλου
Έτσι, το εμβαδόν του εγγεγραμμένου κύκλου θα είναι. Και το πρόβλημα είναι να αποδείξουμε ότι το άθροισμα αυτών των περιοχών είναι ίσο με το εμβαδόν του εσωτερικού κύκλου. Λοιπόν, ας κάνουμε το άθροισμα των περιοχών των κορωνών. Αυτό είναι το άθροισμα των περιοχών των κορωνών. Μπορείτε να δείτε ότι έχουμε 3 κύκλους ακτίνων. Αυτό το άρθρο προτείνει μια υπόθεση, μια πρόφαση για την εξέταση ορισμένων σημείων των μαθηματικών αυτής της περιόδου στη Μεσοποταμία.
Σχηματίζοντας έναν κύκλο ανάμεσα σε δύο εξάγωνα, η περίμετρος του οποίου μπορεί εύκολα να υπολογιστεί και στη συνέχεια διπλασιάζοντας διαδοχικά τον αριθμό των πλευρών, αποκτά ένα πλαίσιο με πολύγωνα με 96 πλευρές. Είναι πιθανώς πιο εύκολο να αξιολογήσετε την απόδοση καθορίζοντας αριθμητικές τιμές.
Δηλαδή, η κάθετη διχοτόμος πρέπει επίσης να διέρχεται από το σημείο, και οι τρεις κάθετες διχοτόμοι τέμνονται σε ένα σημείο.
κατα δευτερον: αν σχεδιάσουμε έναν κύκλο με κέντρο σε σημείο και ακτίνα, τότε και αυτός ο κύκλος θα περάσει από το σημείο και από το σημείο, δηλαδή θα είναι ο περιγεγραμμένος κύκλος. Αυτό σημαίνει ότι υπάρχει ήδη ότι η τομή των τριών κάθετων διχοτόμων είναι το κέντρο του περιγεγραμμένου κύκλου για οποιοδήποτε τρίγωνο.
Βλέπουμε εδώ το ενδιαφέρον και την αποτελεσματικότητα των μεθόδων παρατήρησης: αφενός παρέχουν μια προσέγγιση και, αφετέρου, σας επιτρέπουν να ελέγξετε ένα τέλειο λάθος. Από όσο γνωρίζω, ο Αρχιμήδης είναι ο πρώτος που δικαιολογεί ρητά τα αποτελέσματά του σχετικά με τον κύκλο και δίνει βήμα προς βήμα μια σειρά από επιχειρήματα εξηγώντας γιατί αυτά που ισχυρίζεται είναι αληθινά. Δεν είναι όμως ο πρώτος που ενδιαφέρεται για τον κύκλο και το μέτρο του. Έχουμε πολύ αρχαία στοιχεία, ένα στην Αίγυπτο και μερικά άλλα στη Μεσοποταμία, που πηγαίνουν προς αυτή την κατεύθυνση.
Και υπάρχουν μερικές «βαβυλωνιακές» πήλινες πλάκες που χρονολογούνται από την ίδια περίοδο και κατά μήκος της περιμέτρου ή της περιοχής του δίσκου. Αυτό είναι το θέμα αυτού του άρθρου. Ο περίπατος μπορεί να ξεκινήσει αλλά πριν φύγει για τη Βαβυλώνα 17ος ή 18ος αιώνας π.Χ. Έχει βρεθεί μια βαβυλωνιακή πήλινη πλάκα που δίνει τον λόγο της περιμέτρου ενός εξαγώνου προς την περίμετρο του περιγεγραμμένου κύκλου του.
Και το τελευταίο: για τη μοναδικότητα. Είναι σαφές (σχεδόν) ότι το σημείο μπορεί να ληφθεί με μοναδικό τρόπο, και επομένως ο κύκλος είναι επίσης μοναδικός. Λοιπόν, "σχεδόν" - θα το αφήσουμε στην κρίση σας. Εδώ αποδείξαμε το θεώρημα. Μπορείτε να φωνάξετε "Όρα!".
Και αν το πρόβλημα είναι η ερώτηση "βρες την ακτίνα του περιγεγραμμένου κύκλου"; Ή το αντίστροφο, η ακτίνα είναι δεδομένη, αλλά πρέπει να βρείτε κάτι άλλο; Υπάρχει τύπος που να συσχετίζει την ακτίνα του περιγεγραμμένου κύκλου με τα άλλα στοιχεία ενός τριγώνου;
Και συχνά προστίθενται με τη μια ή την άλλη μορφή. Αυτό ήταν το δεύτερο που μου δημιούργησε ένα πρόβλημα: θα μπορούσαν πραγματικά οι Βαβυλώνιοι να βρουν αυτή την τιμή πειραματικά; Επί του παρόντος, η εμπειρία είναι εύκολη στη χρήση, με μετρητή μοδίστρας και καθημερινά αντικείμενα διαφορετικών διαμέτρων: τηγάνι, κατσαρόλα, τενεκέδες. Μετράται η περίμετρος και η διάμετρος και γίνεται η διαίρεση. Οι διαφορές ήταν στο τρίτο δεκαδικό ψηφίο. Φυσικά, δεν υπάρχουν τόσο ακριβή βιομηχανικά είδη, ούτε μετρητές μοδίστρας βαθμολογημένα σε χιλιοστά.
Για μέτρηση, είναι πιο λεπτό: σχοινί, δερμάτινο λουρί, μπορεί να τεντωθεί υπό τάση και να συστέλλεται άνετα. Από την άλλη πλευρά, ο αποξηραμένος φλοιός παπύρου δεν επιμηκύνεται. Δυστυχώς δεν το είχα. Προφανώς, δεν είναι βαθμολογημένες, αλλά αυτό δεν είναι σοβαρό: μας ενδιαφέρει η αναλογία δύο μηκών: από την περίμετρο και τη διάμετρο, και όχι από τα ίδια τα μήκη. Είναι εύκολο να γυρίσεις ένα αντικείμενο με μπαστούνι και να το κόψεις. Περιέργως, είναι λιγότερο εύκολο να κόψετε με ακρίβεια το νήμα μπαστούνι για να ταιριάζει με τη διάμετρο. Πράγματι, η άνω άκρη της κεραμικής είναι συχνά στρογγυλεμένη.
Πολύ συχνά, όταν λύνετε γεωμετρικά προβλήματα, πρέπει να κάνετε ενέργειες με βοηθητικά σχήματα. Για παράδειγμα, βρείτε την ακτίνα ενός εγγεγραμμένου ή περιγεγραμμένου κύκλου κ.λπ. Αυτό το άρθρο θα σας δείξει πώς να βρείτε την ακτίνα ενός κύκλου που περιβάλλει ένα τρίγωνο. Ή, με άλλα λόγια, η ακτίνα του κύκλου στον οποίο είναι εγγεγραμμένο το τρίγωνο.
Επομένως, είναι απαραίτητο να στερεώσετε το μπαστούνι γύρω από την περίμετρο και στη συνέχεια να κόψετε το δεύτερο μαχαίρι μπαστούνι, που αντιστοιχεί στην εσωτερική διάμετρο του πρώτου. Μένει να υπολογίσουμε την αναλογία των δύο μηκών χωρίς να τα γνωρίζουμε ακριβείς τιμές, το οποίο μπορεί να γίνει επιστρέφοντας στην ίδια την αρχή της διαίρεσης. 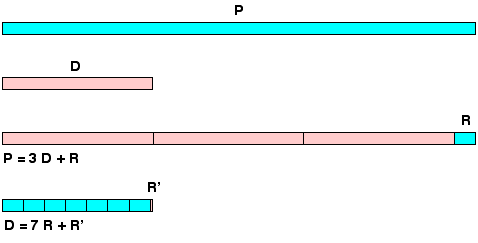
Η καλύτερη μου επίδοση ήταν 6, 8 φορές, δηλαδή 6 φορές, με υπέροχη ξεκούραση. Ωστόσο, αυτά τα πειράματα με έπεισαν ότι οι Βαβυλώνιοι δεν έλαβαν πειραματική αξία, τουλάχιστον όχι από αυτή τη διαδρομή. Σε αυτή την περίπτωση όμως προκύπτουν δύο ερωτήματα.
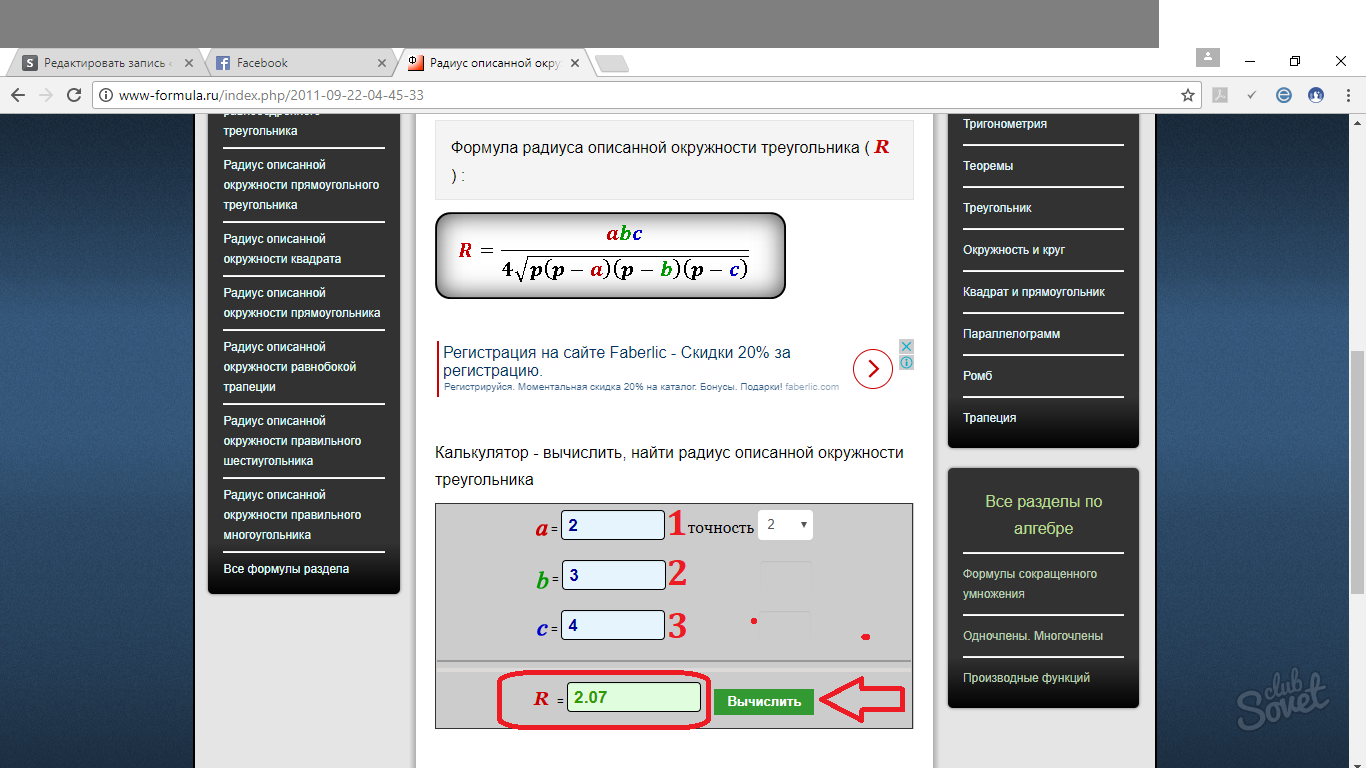
Πώς να βρείτε την ακτίνα ενός κύκλου που περιβάλλεται γύρω από ένα τρίγωνο - ο γενικός τύπος
Ο γενικός τύπος είναι ο εξής: R = abc/4√p(p - a)(p - b)(p - c), όπου R είναι η ακτίνα του περιγεγραμμένου κύκλου, p είναι η περίμετρος του τριγώνου διαιρούμενη με 2 (ημιπερίμετρος). α, β, γ είναι οι πλευρές του τριγώνου.
Να βρείτε την ακτίνα του κύκλου του τριγώνου αν a = 3, b = 6, c = 7.
Ερώτηση 1: Αν δεν είναι πειραματικό, είναι θεωρητικό, γεωμετρικό. 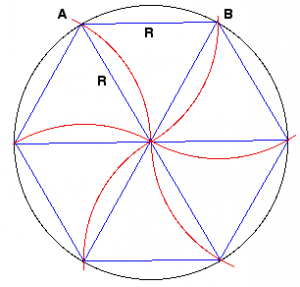
Έτσι, η περίμετρος P ενός κύκλου είναι μεγαλύτερη από αυτή ενός εξαγώνου και η αναλογία μεταξύ τους είναι ίση. Είναι πολύ φυσικό να υπολογίζουμε την περίμετρο ενός κύκλου, άγνωστου σε σχέση με αυτό που είναι γνωστό στο ίδιο το εξάγωνο.
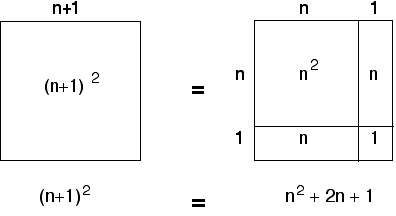
Αργότερα θα δούμε τι να σκεφτούμε για αυτό. Υπόθεση 1: Οι Βαβυλώνιοι γνώριζαν το Πυθαγόρειο Θεώρημα χίλια χρόνια πριν. Υπόθεση 2: Ήξεραν ότι είχαν βρει ορθογώνια με ακέραιες πλευρές. Ίσως όχι όλοι, αλλά τουλάχιστον αυτοί των οποίων η υποτείνουσα και η μία από τις πλευρές είναι ολόκληροι ακέραιοι.
Έτσι, με βάση τον παραπάνω τύπο, υπολογίζουμε την ημιπερίμετρο:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Αντικαταστήστε τις τιμές στον τύπο και λάβετε:
R = 3 x 6 x 7/4√8(8 - 3)(8 - 6)(8 - 7) = 126/4√(8 x 5 x 2 x 1) = 126/4√80 = 126/16 √5.
Απάντηση: R = 126/16√5
Πώς να βρείτε την ακτίνα ενός κύκλου που περικλείεται σε ένα ισόπλευρο τρίγωνο
Για να βρείτε την ακτίνα ενός κύκλου που περικλείεται γύρω από ένα ισόπλευρο τρίγωνο, υπάρχει ένας αρκετά απλός τύπος: R = a/√3, όπου a είναι το μέγεθος της πλευράς του.
Φυσικά, δεν υπάρχει καμία απόδειξη ότι οι Βαβυλώνιοι το έκαναν αυτό. Μόνο η ανακάλυψη μιας νέας πήλινης ταμπλέτας μπορεί να το κάνει αυτό. Επιπλέον, αυτή η ιδέα βασίζεται στην υπόθεση 1 και γνώριζαν πραγματικά οι Βαβυλώνιοι πώς να βρίσκουν τέτοια τρίγωνα; 
Οι τελευταίες 15 γραμμές χωρίζονται σε 4 στήλες, οι δύο πρώτες γραμμές των οποίων ορίζουν το περιεχόμενο. Η στήλη 4 περιέχει το σύμβολο ακολουθούμενο από τους αριθμούς από το 1 έως.
Παράδειγμα: Η πλευρά ενός ισόπλευρου τριγώνου είναι 5. Βρείτε την ακτίνα του περιγεγραμμένου κύκλου.
Δεδομένου ότι όλες οι πλευρές ενός ισόπλευρου τριγώνου είναι ίσες, για να λύσετε το πρόβλημα, πρέπει απλώς να εισαγάγετε την τιμή του στον τύπο. Παίρνουμε: R = 5/√3.
Απάντηση: R = 5/√3.
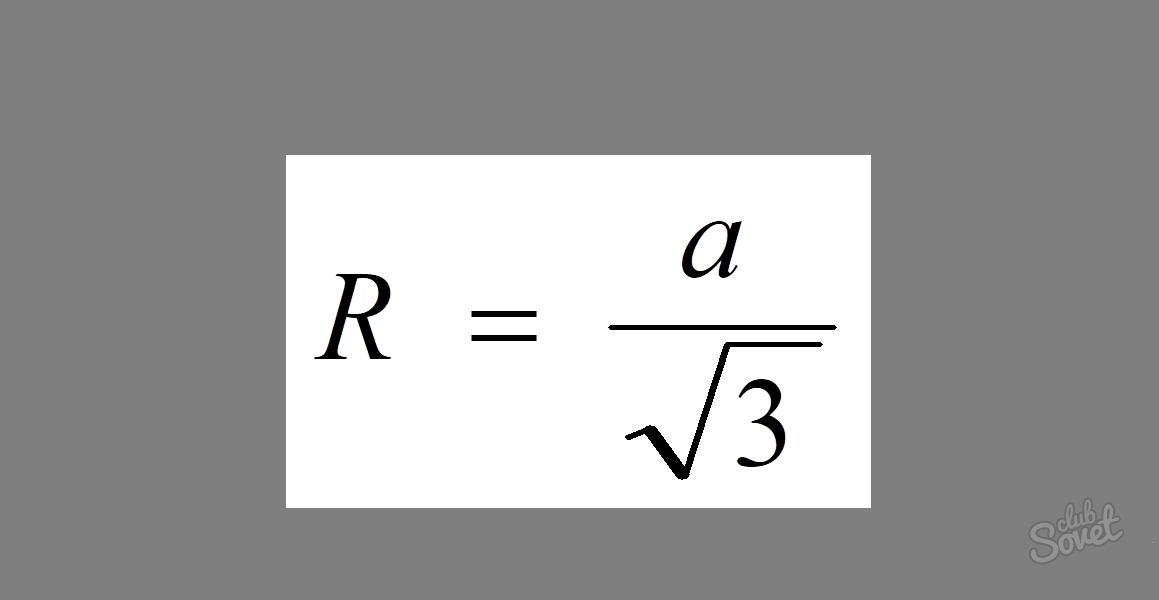
Πώς να βρείτε την ακτίνα ενός κύκλου που περιβάλλεται γύρω από ένα ορθογώνιο τρίγωνο
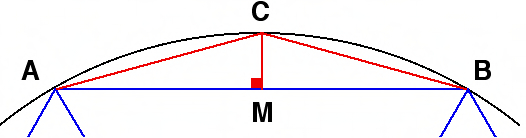
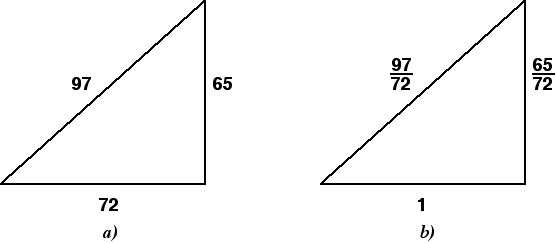
Ο τύπος μοιάζει με αυτό: R = 1/2 × √(a² + b²) = c/2, όπου a και b είναι σκέλη και c είναι η υποτείνουσα. Αν προσθέσουμε τα τετράγωνα των σκελών σε ορθογώνιο τρίγωνο, παίρνουμε το τετράγωνο της υποτείνουσας. Όπως φαίνεται από τον τύπο, αυτή η έκφραση βρίσκεται κάτω από τη ρίζα. Υπολογίζοντας τη ρίζα του τετραγώνου της υποτείνουσας, παίρνουμε το ίδιο το μήκος. Πολλαπλασιάζοντας την παράσταση που προκύπτει με το 1/2 τελικά μας οδηγεί στην παράσταση 1/2 × c = c/2.
Οι στήλες 1, 2 και 3 αναφέρονται σε ορθογώνια τρίγωνα. Οι στήλες 2 και 3 αντίστοιχα δίνουν τη μικρότερη πλευρά και την υποτείνουσα κάθε τριγώνου. Η στήλη 1 δίνει το τετράγωνο της αναλογίας εκατέρωθεν της δεξιάς γωνίας. Για παράδειγμα, η γραμμή 5 ξεκινά στο σεξουαλικό σύστημα.
Αυτό είναι πολύ ακριβές για να είναι αληθινό, αλλά μπορείτε να ελέγξετε ότι είναι το ίδιο και για άλλες χορδές. Υπάρχει διαμάχη σχετικά με τις μεθόδους που θα μπορούσαν να χρησιμοποιούσαν οι Βαβυλώνιοι για να συντάξουν αυτόν τον πίνακα. Υπάρχουν επίσης λάθη στο αντίγραφο του γραφέα και μικρά μυστήρια, όπως η γραμμή 11, που δίνει το 45 και το 1 15 ως πλευρές, δηλαδή στον δεκαδικό αριθμό: 45, και τα δύο είναι πολλαπλάσια του 15, και αυτό το τρίγωνο δεν είναι παρά ένα τρίγωνο των πλευρών. Γιατί δεν δίνεται σε αυτή τη μορφή, πολύ πιο απλό; Και ποιο θα μπορούσε να είναι το πλεονέκτημα να δοθεί το τετράγωνο της κλίσης παρά η ίδια η κλίση;
Παράδειγμα: Υπολογίστε την ακτίνα του περιγεγραμμένου κύκλου εάν τα σκέλη του τριγώνου είναι 3 και 4. Αντικαταστήστε τις τιμές στον τύπο. Παίρνουμε: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2,5.
Σε αυτήν την έκφραση, το 5 είναι το μήκος της υποτείνουσας.
Απάντηση: R = 2,5.
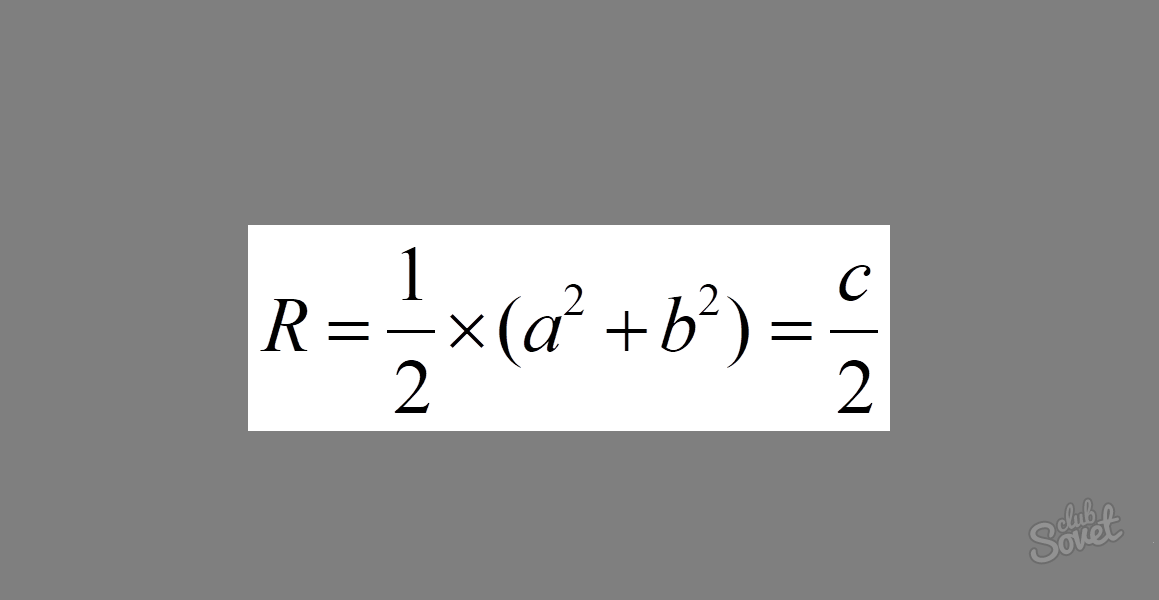
Πώς να βρείτε την ακτίνα ενός κύκλου που περικλείεται γύρω από ένα ισοσκελές τρίγωνο
Ο τύπος μοιάζει με αυτό: R = a² / √ (4a² - b²), όπου a είναι το μήκος του μηρού του τριγώνου και b είναι το μήκος της βάσης.
Παράδειγμα: Υπολογίστε την ακτίνα ενός κύκλου αν ο γοφός του = 7 και η βάση του = 8.
Λύση: Αντικαθιστούμε αυτές τις τιμές στον τύπο και παίρνουμε: R \u003d 7² / √ (4 × 7² - 8²).
R = 49/√(196 - 64) = 49/√132. Η απάντηση μπορεί να γραφτεί κατευθείαν έτσι.
Απάντηση: R = 49/√132
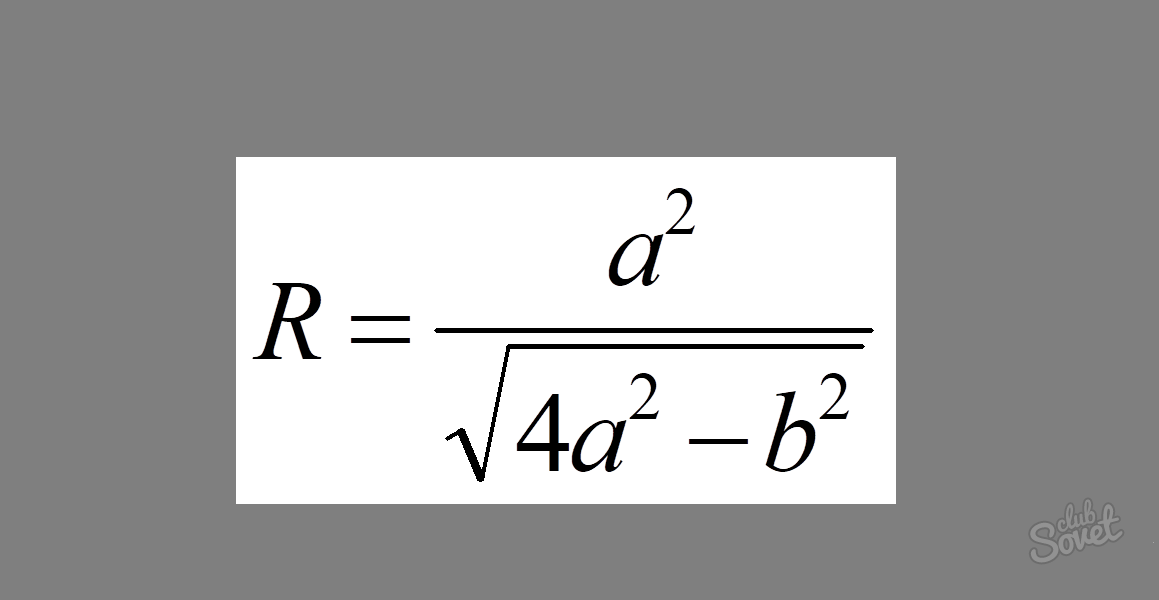
Διαδικτυακοί πόροι για τον υπολογισμό της ακτίνας ενός κύκλου
Είναι πολύ εύκολο να μπερδευτείς σε όλες αυτές τις φόρμουλες. Επομένως, εάν είναι απαραίτητο, μπορείτε να χρησιμοποιήσετε ηλεκτρονικές αριθμομηχανές, που θα σας βοηθήσει στην επίλυση προβλημάτων σχετικά με την εύρεση της ακτίνας. Η αρχή λειτουργίας τέτοιων μίνι προγραμμάτων είναι πολύ απλή. Αντικαταστήστε την τιμή της πλευράς στο κατάλληλο πεδίο και λάβετε μια έτοιμη απάντηση. Μπορείτε να επιλέξετε διάφορες επιλογές για τη στρογγυλοποίηση της απάντησης: σε δεκαδικά, εκατοστά, χιλιοστά κ.λπ.