एक त्रिभुज के परिबद्ध वृत्त का व्यास. पाठ का सारांश "परिक्रमा वृत्त"। किसी त्रिभुज के चारों ओर परिचालित वृत्त की त्रिज्या कैसे ज्ञात करें - सामान्य सूत्र
इस भाग में, हम एक त्रिभुज के चारों ओर (अक्सर "पास" कहा जाता है) परिबद्ध वृत्त पर चर्चा करेंगे। सबसे पहले, आइए एक परिभाषा दें।
1.परिवृत्त वृत्त का अस्तित्व एवं केन्द्र
यहां प्रश्न उठता है: क्या किसी त्रिभुज के लिए ऐसा वृत्त मौजूद है? यह पता चला कि हाँ, सभी के लिए। और इसके अलावा, अब हम एक प्रमेय तैयार करेंगे जो इस प्रश्न का भी उत्तर देता है कि परिचालित वृत्त का केंद्र कहाँ है।
एक आयत के विकर्ण की लंबाई ज्ञात करने के सूत्र
व्यास और कोण β में एक आयत के किनारे का सूत्र। इसे किसी भी खंड के लिए आयत का विकर्ण कहा जाता है जो आयत के विपरीत कोनों के दो शीर्षों को जोड़ता है। आयत की दोनों भुजाओं के संदर्भ में एक आयत के विकर्ण का सूत्र।
क्षेत्रफल और दोनों तरफ एक आयत के विकर्ण का सूत्र। परिधि और दोनों तरफ एक आयत के विकर्ण का सूत्र। परिचालित वृत्त की त्रिज्या के संदर्भ में एक आयत के विकर्ण का सूत्र। एक वृत्त की परिधि के अनुदिश एक आयत के विकर्ण का सूत्र।
ऐसे दिखते हैं:
आइए साहस जुटाएं और इस प्रमेय को सिद्ध करें। यदि आपने पहले ही विषय "" पढ़ लिया है और यह समझ लिया है कि तीन समद्विभाजक एक बिंदु पर क्यों प्रतिच्छेद करते हैं, तो यह आपके लिए आसान होगा, लेकिन यदि आपने इसे नहीं पढ़ा है, तो चिंता न करें: अब हम यह सब समझेंगे बाहर।
हम बिन्दुपथ (एलपीटी) की अवधारणा का उपयोग करके प्रमाण प्रस्तुत करेंगे।
एक आयत के विकर्ण का सूत्र, विकर्ण से सटे कोण की ज्या और उस कोण के विपरीत भुजा की लंबाई के संदर्भ में। किसी आयत के विकर्ण का सूत्र, विकर्ण से सटे कोण की कोज्या और उस कोण से सटे भुजा की लंबाई के संदर्भ में। विकर्णों और आयत के क्षेत्रफल के बीच न्यून कोण की ज्या के पदों में एक आयत के विकर्ण का सूत्र।
एक आयत की परिधि की लंबाई निर्धारित करने के सूत्र
किसी आयत का परिमाप उसकी सभी भुजाओं की लंबाई के योग को कहा जाता है। आयत की दोनों भुजाओं के संदर्भ में एक आयत की परिधि का सूत्र। क्षेत्रफल और दोनों भुजाओं को देखते हुए एक आयत की परिधि का सूत्र। एक आयत के विकर्ण और दोनों तरफ के परिमाप का सूत्र।
खैर, उदाहरण के लिए, क्या गेंदों का सेट गोल वस्तुओं का "ज्यामितीय स्थान" है? नहीं, बिल्कुल, क्योंकि वहाँ गोल हैं...तरबूज। लेकिन क्या लोगों का एक समूह, एक "ज्यामितीय स्थान", बोलने में सक्षम है? न ही, क्योंकि ऐसे बच्चे हैं जो बोल नहीं सकते। जीवन में, वास्तविक "बिंदुओं के ज्यामितीय स्थान" का उदाहरण ढूंढना आम तौर पर मुश्किल होता है। ज्यामिति आसान है. उदाहरण के लिए, यहाँ वही है जो हमें चाहिए:
परिचालित वृत्त की त्रिज्या और दोनों तरफ के संदर्भ में एक आयत की परिधि का सूत्र। एक आयत की परिधि का सूत्र, परिचालित वृत्त और दोनों भुजाओं का व्यास दिया गया है। इसे आयत की भुजाओं से घिरे स्थान में, अर्थात् आयत के परिधि क्षेत्र के अंदर, आयत का क्षेत्रफल कहा जाता है।
एक आयत का क्षेत्रफल ज्ञात करने के सूत्र
दो भुजाओं वाले एक आयत के क्षेत्रफल का सूत्र। परिधि और दोनों तरफ एक आयत के क्षेत्रफल का सूत्र। एक आयत के विकर्ण और दोनों तरफ के क्षेत्रफल का सूत्र। विकर्ण के अनुदिश एक आयत के क्षेत्रफल और विकर्णों के बीच न्यून कोण की ज्या का सूत्र।
यहां सेट मध्य लंबवत है, और संपत्ति "" खंड के सिरों से समान दूरी (बिंदु) होना है।
की जाँच करें? तो, आपको दो बातें सुनिश्चित करनी होंगी:
के साथ और साथ से जुड़ें। फिर रेखा मध्य और ऊंचाई है। तो, - समद्विबाहु, - हमने यह सुनिश्चित किया कि लंबवत समद्विभाजक पर स्थित कोई भी बिंदु बिंदुओं से समान रूप से दूर हो।
वृत्त एक आयत के चारों ओर घिरा हुआ है
परिचालित वृत्त और किसी भी भुजा की त्रिज्या को देखते हुए एक आयत के क्षेत्रफल का सूत्र। एक वृत्त में एक आयत के क्षेत्रफल का सूत्र एक वृत्त के दोनों ओर एक वृत्त है। इसे एक आयत के चारों ओर घिरा हुआ वृत्त कहा जाता है, जो आयत के चारों शीर्षों से होकर गुजरता है, जिसका केंद्र आयत के विकर्णों का प्रतिच्छेदन होता है।
एक आयत के चारों ओर परिचालित वृत्त की त्रिज्या ज्ञात करने के सूत्र
दो भुजाओं वाले एक आयत से घिरे वृत्त की त्रिज्या का सूत्र। वर्ग की परिधि और दोनों ओर एक आयत के चारों ओर परिचालित वृत्त की त्रिज्या का सूत्र। एक आयत के चारों ओर वर्णित वृत्त की त्रिज्या का सूत्र आयत के क्षेत्रफल और उसकी एक भुजा की लंबाई के संदर्भ में वर्णित है।
लो - मध्य और कनेक्ट करें और। माध्यिका प्राप्त हुई। लेकिन - स्थिति के अनुसार समद्विबाहु, न केवल माध्यिका, बल्कि ऊंचाई, यानी माध्यिका लंबवत भी। इसका मतलब यह है कि बिंदु बिल्कुल लम्ब समद्विभाजक पर स्थित है।
सभी! हमने इस तथ्य को पूरी तरह से सत्यापित कर लिया है कि किसी खंड का लंबवत समद्विभाजक खंड के सिरों से समान दूरी पर स्थित बिंदुओं का स्थान है।
आयत के विकर्ण के अनुदिश एक आयत के चारों ओर परिचालित वृत्त की त्रिज्या का सूत्र। वृत्त की परिधि के व्यास द्वारा एक आयत के चारों ओर वर्णित वृत्त की त्रिज्या का सूत्र। एक आयत के चारों ओर वर्णित वृत्त की त्रिज्या का सूत्र विकर्ण से सटे कोण की ज्या और इस कोण के विपरीत भुजा की लंबाई के संदर्भ में वर्णित है।
दिए गए बहुभुज के चारों ओर का वृत्त परिबद्ध वृत्त है। अधिकांश लोगों ने परिधि और त्रिज्या शब्द सुने हैं, लेकिन परिबद्ध वृत्त एक कम परिचित शब्द है। एक त्रिभुज की तरह सीधी भुजाओं वाले 2D बहुभुज की कल्पना करें। एक त्रिभुज के चारों ओर एक वृत्त की कल्पना करें ताकि वह इसके तीनों शीर्षों को छू सके; यह एक सीमित दायरा है. अपनी त्रिज्या की गणना करने के लिए, बस कुछ सरल बीजगणित और एक कैलकुलेटर का उपयोग करें।
यह सब ठीक है और अच्छा है, लेकिन क्या हम परिचालित घेरे के बारे में भूल गए हैं? बिलकुल नहीं, हमने बस खुद को "हमले के लिए पुलहेड" तैयार किया है।
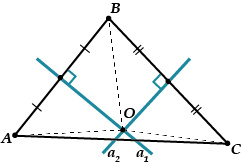
एक त्रिभुज पर विचार करें. आइए दो मध्य लंब बनाएं और, कहें, खंडों पर और। वे किसी बिंदु पर प्रतिच्छेद करेंगे, जिसे हम नाम देंगे।
अपने सभी मापों की जांच करें और सुनिश्चित करें कि जब आप चक्कर लगा रहे हों तो कम्पास का कहना है कि यह नहीं बदलता है।
- सटीक एवं सटीकता से माप करना अत्यंत महत्वपूर्ण है।
- सभी बहुभुजों में एक घिरा हुआ वृत्त नहीं हो सकता।
इस प्रकार, एक षट्भुज में अंकित वृत्त का क्षेत्रफल बराबर होता है। अब हम अंकित वर्ग की ओर मुड़ते हैं। चूँकि वर्ग का विकर्ण मूल समय की भुजा के बराबर है, हमारे पास है। तब एक वर्ग में अंकित वृत्त की त्रिज्या भुजा की आधी माप होगी। इस प्रकार, आप देखेंगे कि त्रिभुज में अंकित वृत्त की त्रिज्या, त्रिभुज में घिरे वृत्त की त्रिज्या की आधी है, क्योंकि वृत्त की परिधि को 1 के अनुपात में दो भागों में विभाजित माध्यम द्वारा वर्णित किया गया है, और फिर त्रिज्या अंकित वृत्त का होगा.
और अब, ध्यान!
बिंदु लंब समद्विभाजक पर स्थित है;
बिंदु लम्ब समद्विभाजक पर स्थित है।
और इसका मतलब है और.
इससे कई बातें सामने आती हैं:
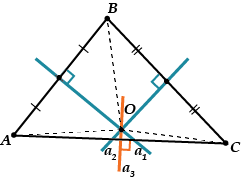
पहले तो, बिंदु को खंड के तीसरे लंबवत समद्विभाजक पर स्थित होना चाहिए।
वृत्त माप और सन्निकटन
अत: अंकित वृत्त का क्षेत्रफल होगा। और समस्या यह सिद्ध करने की है कि इन क्षेत्रों का योग आंतरिक वृत्त के क्षेत्रफल के बराबर है। तो, आइए मुकुटों के क्षेत्रफलों का योग करें। यह मुकुटों के क्षेत्रफलों का योग है। आप देख सकते हैं कि हमारे पास किरणों के 3 वृत्त हैं। यह लेख मेसोपोटामिया में इस अवधि के गणित के कुछ बिंदुओं पर विचार करने के लिए एक परिकल्पना, एक बहाना प्रस्तावित करता है।
दो षट्भुजों के बीच एक वृत्त बनाकर, जिसकी परिधि की गणना आसानी से की जा सकती है, फिर भुजाओं की संख्या को क्रमिक रूप से दोगुना करके, वह 96 भुजाओं वाले बहुभुजों वाला एक फ्रेम प्राप्त करता है। संख्यात्मक मान निर्दिष्ट करके प्रदर्शन का मूल्यांकन करना संभवतः आसान है।
अर्थात्, लम्ब समद्विभाजक को भी बिंदु से गुजरना होगा, और तीनों लम्ब समद्विभाजक एक बिंदु पर प्रतिच्छेद करते हैं।
दूसरे: यदि हम एक वृत्त खींचते हैं जिसका केंद्र एक बिंदु और त्रिज्या पर है, तो यह वृत्त भी बिंदु से होकर गुजरेगा, अर्थात यह परिचालित वृत्त होगा। इसका मतलब यह है कि यह पहले से ही मौजूद है कि तीन लंबवत समद्विभाजकों का प्रतिच्छेदन किसी भी त्रिभुज के लिए परिबद्ध वृत्त का केंद्र है।
हम यहां अवलोकन विधियों की रुचि और प्रभावशीलता देखते हैं: एक ओर, वे एक अनुमान प्रदान करते हैं, और दूसरी ओर, वे आपको एक सही गलती को नियंत्रित करने की अनुमति देते हैं। जहाँ तक मुझे पता है, आर्किमिडीज़ वृत्त के संबंध में अपने परिणामों को स्पष्ट रूप से उचित ठहराने वाले पहले व्यक्ति हैं, और चरण दर चरण तर्कों की एक श्रृंखला देते हैं जो बताते हैं कि उनका दावा सच क्यों है। लेकिन वह पहले व्यक्ति नहीं हैं जिनकी वृत्त और उसकी माप में रुचि है। हमारे पास बहुत प्राचीन साक्ष्य हैं, एक मिस्र में और कुछ अन्य मेसोपोटामिया में, जो उस दिशा में जा रहे हैं।
और कुछ "बेबीलोनियन" मिट्टी की गोलियाँ हैं जो उसी अवधि की हैं और डिस्क की परिधि या क्षेत्र के आसपास हैं। यही इस लेख का विषय है. पैदल यात्रा 17वीं या 18वीं शताब्दी ईसा पूर्व बेबीलोन के लिए रवाना होने से पहले शुरू हो सकती है। एक बेबीलोनियाई मिट्टी की गोली मिली है जो एक षट्भुज की परिधि और उसके परिबद्ध वृत्त की परिधि का अनुपात बताती है।
और आखिरी बात: विशिष्टता के बारे में. यह स्पष्ट (लगभग) है कि बिंदु को एक अनूठे तरीके से प्राप्त किया जा सकता है, और इसलिए वृत्त भी अद्वितीय है। खैर, "लगभग" - हम इसे आप पर छोड़ देंगे। यहां हमने प्रमेय को सिद्ध कर दिया है। आप "हुर्रे!" चिल्ला सकते हैं।
और यदि समस्या "परिवृत्त वृत्त की त्रिज्या ज्ञात करें" प्रश्न है? या इसके विपरीत, त्रिज्या दी गई है, लेकिन आपको कुछ और खोजने की ज़रूरत है? क्या परिचालित वृत्त की त्रिज्या को त्रिभुज के अन्य तत्वों से संबंधित करने का कोई सूत्र है?
और इन्हें अक्सर किसी न किसी रूप में जोड़ा जाता है। यह दूसरा था जिसने मुझे एक समस्या दी: क्या बेबीलोनवासी वास्तव में प्रयोगात्मक रूप से इस मूल्य को पा सकते थे? वर्तमान में, सीमस्ट्रेस मीटर और विभिन्न व्यास की रोजमर्रा की वस्तुओं के साथ अनुभव का उपयोग करना आसान है: फ्राइंग पैन, सॉस पैन, टिन के डिब्बे। परिधि और व्यास को मापा जाता है और विभाजन किया जाता है। अंतर दशमलव के तीसरे स्थान पर था। निःसंदेह, ऐसी कोई सटीक औद्योगिक वस्तुएँ नहीं हैं, न ही सीमस्ट्रेस के मीटरों को मिलीमीटर में वर्गीकृत किया गया है।
माप के लिए, यह पतला है: रस्सी, चमड़े का पट्टा, तनाव के तहत खिंच सकता है और आराम से सिकुड़ सकता है। दूसरी ओर, सूखे पपीरस की छाल लम्बी नहीं होती है। दुर्भाग्य से, मेरे पास यह नहीं था। जाहिर है, वे स्नातक नहीं हैं, लेकिन यह गंभीर नहीं है: हम दो लंबाई के अनुपात में रुचि रखते हैं: परिधि और व्यास से, और स्वयं लंबाई से नहीं। रतन से किसी वस्तु के चारों ओर घूमना और उसे काटना आसान है। दिलचस्प बात यह है कि व्यास से मेल खाने के लिए रतन धागे को सटीक रूप से काटना कम आसान है। दरअसल, मिट्टी के बर्तनों का ऊपरी किनारा अक्सर गोल होता है।
अक्सर, ज्यामितीय समस्याओं को हल करते समय, आपको सहायक आकृतियों के साथ कार्य करना पड़ता है। उदाहरण के लिए, किसी खुदे हुए या परिबद्ध वृत्त की त्रिज्या ज्ञात करें, आदि। यह लेख आपको दिखाएगा कि त्रिभुज के चारों ओर स्थित वृत्त की त्रिज्या कैसे ज्ञात करें। या, दूसरे शब्दों में, उस वृत्त की त्रिज्या जिसमें त्रिभुज अंकित है।
इसलिए, परिधि के चारों ओर रतन को ठीक करना आवश्यक है, और फिर पहले के आंतरिक व्यास के अनुरूप दूसरे रतन चाकू को काटें। यह दोनों लंबाई को जाने बिना उनके अनुपात की गणना करने के लिए बना हुआ है सटीक मान, जो विभाजन के मूल स्रोत पर लौटकर किया जा सकता है। 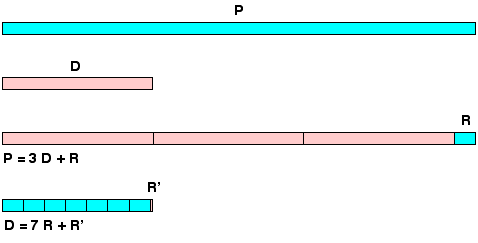
मेरा सर्वश्रेष्ठ प्रदर्शन 6, 8 बार, यानी 6 बार, एक अद्भुत विश्राम के साथ था। हालाँकि, इन प्रयोगों ने मुझे आश्वस्त किया कि बेबीलोनियों को प्रायोगिक मूल्य प्राप्त नहीं हुआ, कम से कम इस मार्ग से नहीं। लेकिन इस मामले में दो सवाल उठते हैं.
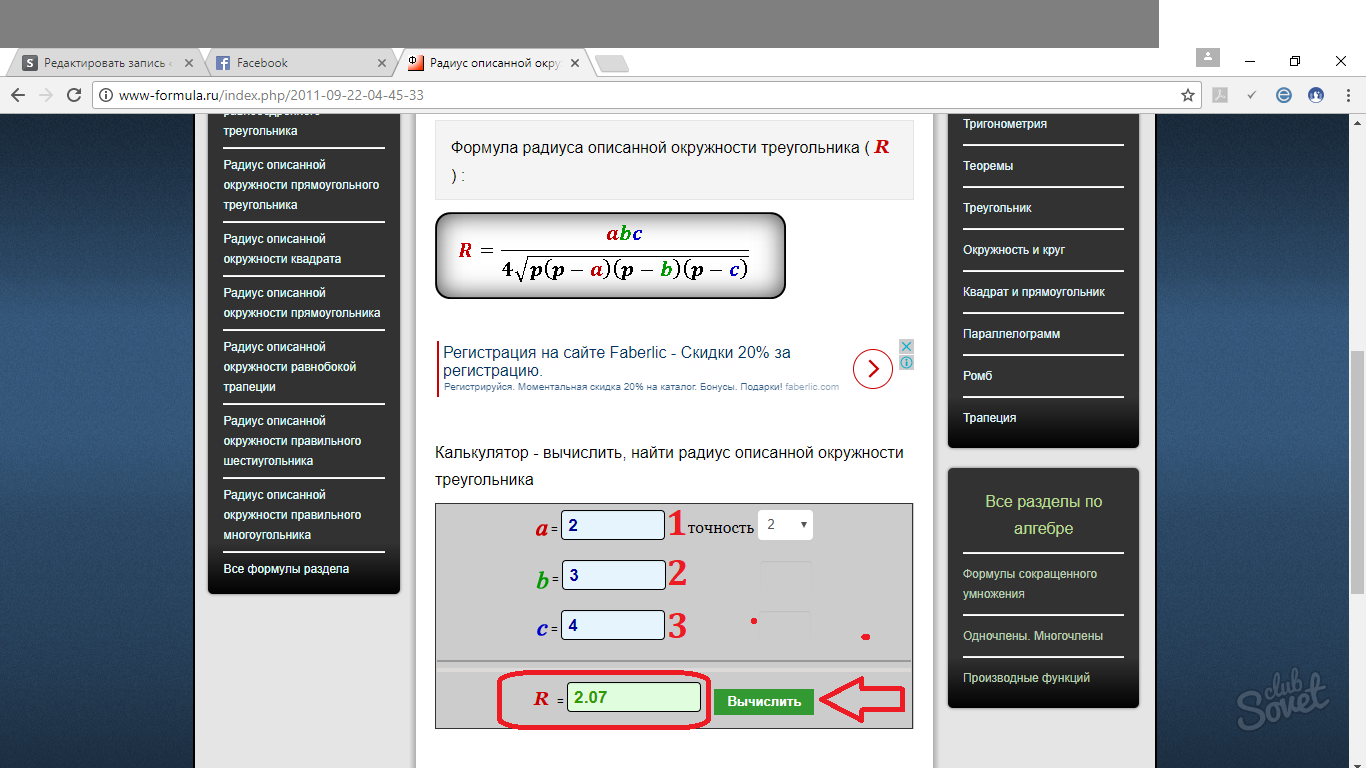
किसी त्रिभुज के चारों ओर परिचालित वृत्त की त्रिज्या कैसे ज्ञात करें - सामान्य सूत्र
सामान्य सूत्र इस प्रकार है: R = abc/4√p(p - a)(p - b)(p - c), जहां R परिचालित वृत्त की त्रिज्या है, p 2 से विभाजित त्रिभुज की परिधि है (आधा-परिधि)। a, b, c त्रिभुज की भुजाएँ हैं।
यदि a = 3, b = 6, c = 7 है तो त्रिभुज के परिवृत्त की त्रिज्या ज्ञात कीजिए।
प्रश्न 1: यदि यह प्रयोगात्मक नहीं है, तो यह सैद्धांतिक, ज्यामितीय है। 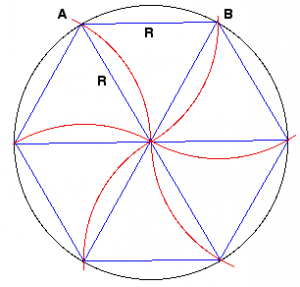
इस प्रकार, एक वृत्त की परिधि P एक षट्भुज की परिधि से अधिक है, और उनके बीच का अनुपात बराबर है। हमारे लिए किसी वृत्त की परिधि का अनुमान लगाना बिल्कुल स्वाभाविक है, जो कि षट्भुज के संबंध में अज्ञात है।
बाद में देखेंगे कि इस बारे में क्या सोचना है. परिकल्पना 1: बेबीलोनवासी पाइथागोरस प्रमेय को एक हजार साल पहले से जानते थे। परिकल्पना 2: वे जानते थे कि उन्हें पूर्णांक भुजाओं वाले आयत मिल गए हैं। शायद सभी नहीं, लेकिन कम से कम वे जिनका कर्ण और एक भुजा पूर्णांक हैं।
इस प्रकार, उपरोक्त सूत्र के आधार पर, हम अर्ध-परिधि की गणना करते हैं:
पी = (ए + बी + सी)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
सूत्र में मानों को प्रतिस्थापित करें और प्राप्त करें:
आर = 3 x 6 x 7/4√8(8 - 3)(8 - 6)(8 - 7) = 126/4√(8 x 5 x 2 x 1) = 126/4√80 = 126/16 √5.
उत्तर: आर = 126/16√5
एक समबाहु त्रिभुज के चारों ओर परिचालित वृत्त की त्रिज्या कैसे ज्ञात करें
एक समबाहु त्रिभुज के चारों ओर परिचालित वृत्त की त्रिज्या ज्ञात करने के लिए, एक काफी सरल सूत्र है: R = a/√3, जहां a इसकी भुजा का आकार है।
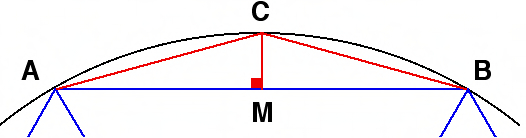
बेशक, इस बात का कोई सबूत नहीं है कि बेबीलोनियों ने ऐसा किया था। केवल नई मिट्टी की गोली की खोज ही ऐसा कर सकती है। इसके अलावा, यह विचार परिकल्पना 1 पर आधारित है और क्या बेबीलोनवासी वास्तव में जानते थे कि ऐसे त्रिकोण कैसे खोजे जाते हैं? 
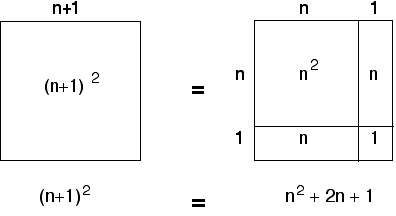
अंतिम 15 पंक्तियों को 4 स्तंभों में विभाजित किया गया है, जिनमें से पहली दो पंक्तियाँ सामग्री को परिभाषित करती हैं। कॉलम 4 में चिह्न के बाद 1 से लेकर तक की संख्याएँ शामिल हैं।
उदाहरण: एक समबाहु त्रिभुज की भुजा 5 है। परिबद्ध वृत्त की त्रिज्या ज्ञात कीजिए।
चूँकि एक समबाहु त्रिभुज की सभी भुजाएँ समान होती हैं, समस्या को हल करने के लिए, आपको बस सूत्र में इसका मान दर्ज करना होगा। हमें मिलता है: R = 5/√3.
उत्तर: आर = 5/√3.
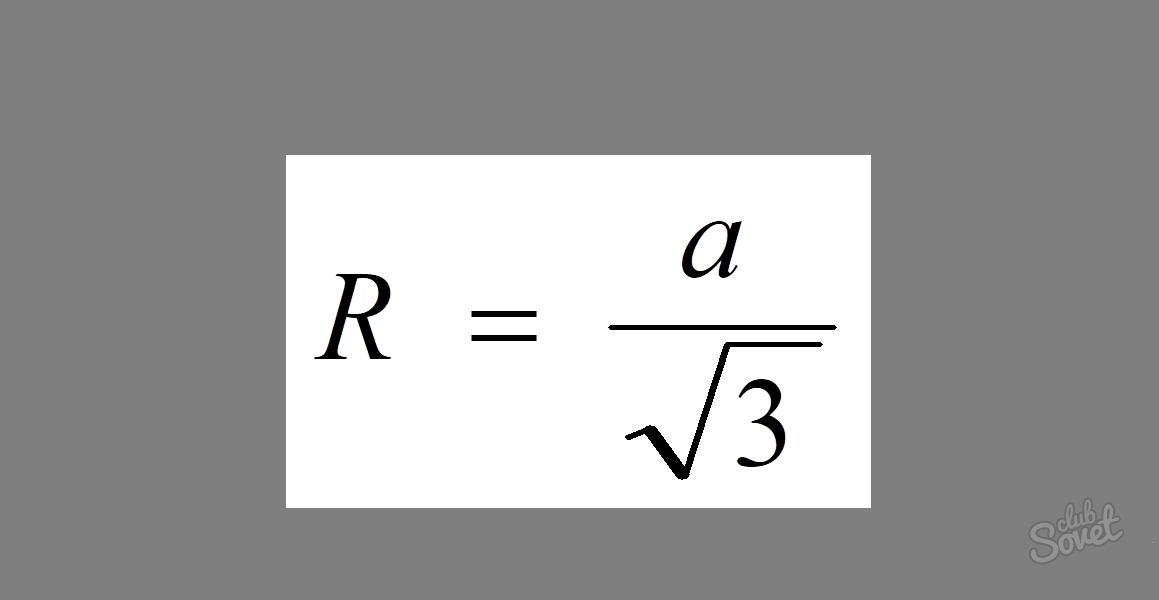
एक समकोण त्रिभुज के चारों ओर परिचालित वृत्त की त्रिज्या कैसे ज्ञात करें
सूत्र इस तरह दिखता है: R = 1/2 × √(a² + b²) = c/2, जहां a और b पैर हैं और c कर्ण है। यदि हम किसी समकोण त्रिभुज में पैरों के वर्गों को जोड़ते हैं, तो हमें कर्ण का वर्ग प्राप्त होता है। जैसा कि सूत्र से देखा जा सकता है, यह अभिव्यक्ति मूल के अंतर्गत है। कर्ण के वर्ग के मूल की गणना करने से हमें लंबाई ही प्राप्त होती है। परिणामी व्यंजक को 1/2 से गुणा करने पर अंततः हमें व्यंजक 1/2 × c = c/2 प्राप्त होता है।
कॉलम 1, 2 और 3 समकोण त्रिभुजों को संदर्भित करते हैं। कॉलम 2 और 3 क्रमशः प्रत्येक त्रिभुज की सबसे छोटी भुजा और कर्ण देते हैं। कॉलम 1 दाएं कोने के दोनों ओर अनुपात का वर्ग देता है। उदाहरण के लिए, पंक्ति 5 यौन प्रणाली से शुरू होती है।
यह सत्य होने के लिए बहुत सटीक है, लेकिन आप जाँच सकते हैं कि यह अन्य स्ट्रिंग्स के लिए भी समान है। इस तालिका को संकलित करने के लिए बेबीलोनियों ने जिन तरीकों का उपयोग किया होगा, उनके बारे में विवाद है। लेखक की प्रतिलिपि में त्रुटियां और छोटे रहस्य भी हैं, जैसे पंक्ति 11, जो 45 और 1 15 को भुजाओं के रूप में देता है, यानी दशमलव संख्या में: 45, और दोनों 15 के गुणज हैं, और यह त्रिकोण एक त्रिकोण के अलावा और कुछ नहीं है पक्षों का. इसे इस अधिक सरल रूप में क्यों नहीं दिया जाता? और ढलान के बजाय ढलान का वर्ग देने से क्या फायदा हो सकता है?
उदाहरण: यदि त्रिभुज के पैर 3 और 4 हैं तो परिचालित वृत्त की त्रिज्या की गणना करें। मानों को सूत्र में रखें। हमें मिलता है: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2.5.
इस अभिव्यक्ति में, 5 कर्ण की लंबाई है।
उत्तर: आर = 2.5.
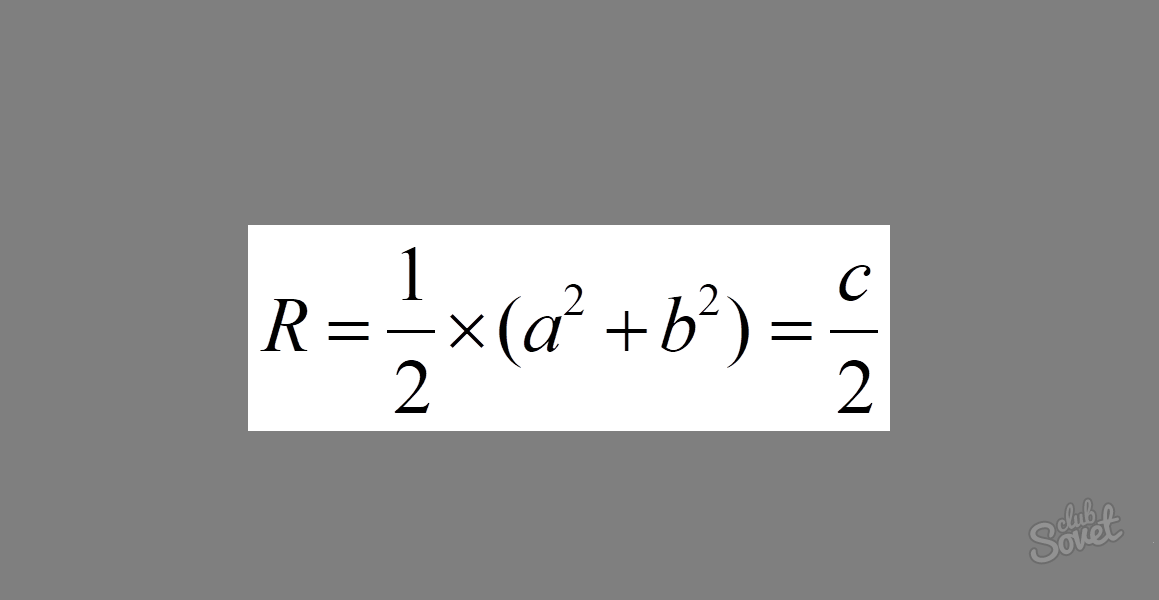
एक समद्विबाहु त्रिभुज के चारों ओर परिचालित वृत्त की त्रिज्या कैसे ज्ञात करें
सूत्र इस तरह दिखता है: R = a² / √ (4a² - b²), जहां a त्रिभुज की जांघ की लंबाई है और b आधार की लंबाई है।
उदाहरण: एक वृत्त की त्रिज्या की गणना करें यदि उसका कूल्हा = 7 और उसका आधार = 8 है।
समाधान: हम इन मानों को सूत्र में प्रतिस्थापित करते हैं और प्राप्त करते हैं: R = 7² / √ (4 × 7² - 8²)।
आर = 49/√(196 - 64) = 49/√132। उत्तर सीधे इस प्रकार लिखा जा सकता है।
उत्तर: आर = 49/√132
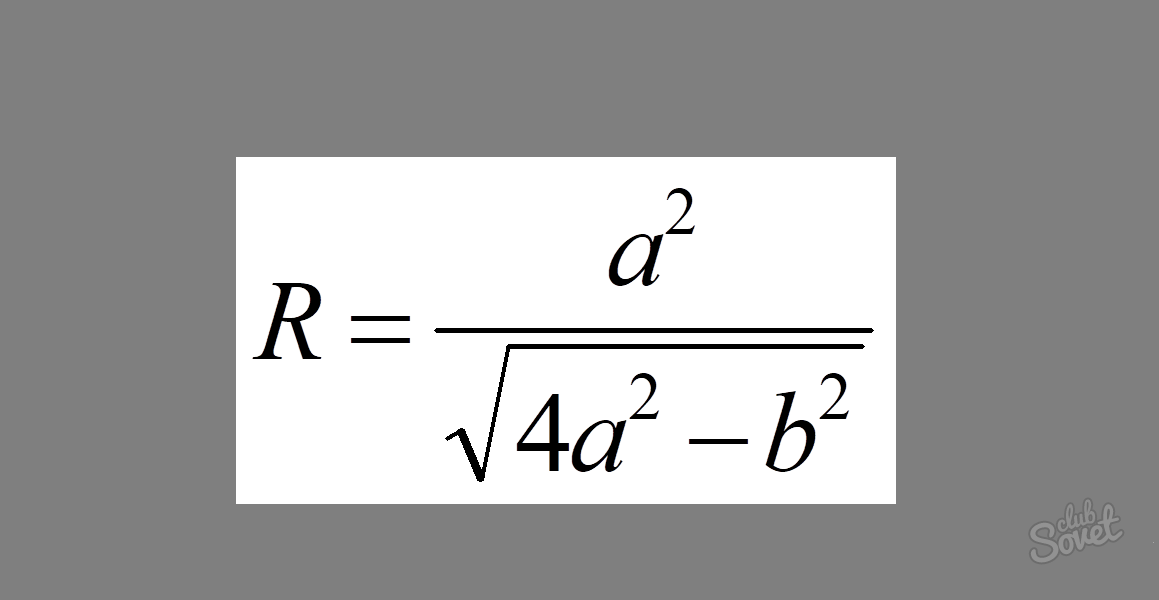
किसी वृत्त की त्रिज्या की गणना के लिए ऑनलाइन संसाधन
इन सभी फॉर्मूलों में उलझना बहुत आसान है. इसलिए, यदि आवश्यक हो, तो आप उपयोग कर सकते हैं ऑनलाइन कैलकुलेटर, जो त्रिज्या ज्ञात करने में आने वाली समस्याओं को हल करने में आपकी सहायता करेगा। ऐसे लघु कार्यक्रमों के संचालन का सिद्धांत बहुत सरल है। पक्ष के मान को उपयुक्त फ़ील्ड में रखें और तैयार उत्तर प्राप्त करें। आप उत्तर को पूर्णांकित करने के लिए कई विकल्प चुन सकते हैं: दशमलव, सौवां, हज़ारवां, आदि।