Średnica okręgu opisanego na trójkącie. Podsumowanie lekcji „określony okrąg”. Jak znaleźć promień koła opisanego na trójkącie - wzór ogólny
W tej części omówimy opisany okrąg wokół (często mówionego „blisko”) trójkąta. Przede wszystkim podajmy definicję.
1. Istnienie i środek okręgu opisanego
Tu pojawia się pytanie: czy taki okrąg istnieje dla dowolnego trójkąta? Okazuje się, że tak, dla każdego. Co więcej, sformułujemy teraz twierdzenie, które odpowiada również na pytanie, gdzie znajduje się środek opisanego okręgu.
Wzory na znalezienie długości przekątnej prostokąta
Formuła na boku prostokąta o średnicy i kącie β. Nazywa się to przekątną prostokąta dla dowolnego odcinka, który łączy dwa wierzchołki przeciwległych rogów prostokąta. Wzór na przekątną prostokąta pod względem dwóch boków prostokąta.
Wzór na przekątną prostokąta w polu i po obu stronach. Wzór na przekątną prostokąta wzdłuż obwodu i po obu stronach. Wzór na przekątną prostokąta pod względem promienia opisanego koła. Wzór na przekątną prostokąta wzdłuż obwodu koła.
Wygląda jak to:
Zbierzmy się na odwagę i udowodnijmy to twierdzenie. Jeśli już przeczytałeś temat „”, zorientowałeś się, dlaczego trzy dwusieczne przecinają się w jednym punkcie, będzie ci łatwiej, ale jeśli go nie przeczytałeś, nie martw się: teraz wszystko wymyślimy na zewnątrz.
Dowód przeprowadzimy z wykorzystaniem koncepcji miejsca punktów (LPT).
Wzór na przekątną prostokąta wyrażony jako sinus kąta przylegającego do przekątnej i długość boku przeciwległego do tego kąta. Wzór na przekątną prostokąta wyrażony cosinusem kąta przylegającego do przekątnej i długością boku przylegającego do tego kąta. Wzór na przekątną prostokąta pod względem sinusa kąta ostrego między przekątnymi a polem prostokąta.
Wzory do wyznaczania długości obwodu prostokąta
Obwód prostokąta nazywamy sumą długości wszystkich boków prostokąta. Wzór na obwód prostokąta pod względem dwóch boków prostokąta. Wzór na obwód prostokąta, mając dane pole i oba boki. Wzór na obwód prostokąta wzdłuż przekątnej i po obu stronach.
No właśnie, czy zbiór kulek to „geometryczne miejsce” okrągłych przedmiotów? Nie, oczywiście, bo są okrągłe... arbuzy. Ale czy zbiór ludzi, „miejsce geometryczne” jest w stanie mówić? Żadne, ponieważ są dzieci, które nie potrafią mówić. W życiu na ogół trudno jest znaleźć przykład prawdziwego „geometrycznego miejsca punktów”. Geometria jest prostsza. Oto, na przykład, właśnie to, czego potrzebujemy:
Wzór na obwód prostokąta pod względem promienia opisanego koła i po obu stronach. Wzór na obwód prostokąta, biorąc pod uwagę średnicę opisanego koła i oba boki. Nazywa się to obszarem prostokąta w przestrzeni ograniczonej bokami prostokąta, to znaczy wewnątrz obszaru obwodu prostokąta.
Wzory do określania pola prostokąta
Wzór na pole prostokąta o dwóch bokach. Wzór na pole prostokąta wzdłuż obwodu i po obu stronach. Wzór na pole prostokąta wzdłuż przekątnej i po obu stronach. Wzór na pole prostokąta wzdłuż przekątnej i sinus kąta ostrego między przekątnymi.
Tutaj zestaw jest środkową prostopadłą, a właściwość „” to „być w równej odległości (punkt) od końców odcinka”.
Sprawdźmy? Musisz więc upewnić się co do dwóch rzeczy:
Połącz z i z. Wtedy linia jest medianą, a wysokość w. Tak więc - równoramienny - upewniliśmy się, że każdy punkt leżący na prostopadłej dwusiecznej jest jednakowo oddalony od punktów i.
Okrąg ograniczony wokół prostokąta
Wzór na pole prostokąta, biorąc pod uwagę promień opisanego koła i dowolny bok. Wzór na pole prostokąta w okręgu to okrąg koła i po obu stronach. Nazywa się to kołem ograniczonym wokół prostokąta, do koła przechodzącego przez cztery wierzchołki prostokąta, którego środek jest przecięciem przekątnych prostokąta.
Wzory na znalezienie promienia koła opisanego na prostokącie
Wzór na promień okręgu ograniczonego prostokątem przechodzącym przez dwa boki. Wzór na promień okręgu opisanego na prostokącie wzdłuż obwodu kwadratu i po obu stronach. Wzór na promień okręgu opisanego wokół prostokąta pod względem pola prostokąta i długości jednego z jego boków.
Weź - środek i połącz i. Dostałem medianę. Ale - równoramienne z warunku, nie tylko środkowa, ale także wysokość, czyli środkowa prostopadła. Oznacza to, że punkt leży dokładnie na dwusiecznej prostopadłej.
Wszystko! W pełni zweryfikowaliśmy fakt, że dwusieczna prostopadła do odcinka jest miejscem geometrycznym punktów równoodległych od końców odcinka.
Wzór na promień okręgu opisanego na prostokącie wzdłuż przekątnej prostokąta. Wzór na promień okręgu opisanego wokół prostokąta średnicą obwodową koła. Wzór na promień okręgu opisanego wokół prostokąta za pomocą sinusa kąta przylegającego do przekątnej i długości boku przeciwległego do tego kąta.
Okrąg otaczający dany wielokąt jest okręgiem opisanym. Większość ludzi słyszała terminy obwód i promień, ale koło ograniczone jest terminem mniej znanym. Wyobraź sobie wielokąt 2D z prostymi bokami, jak trójkąt. Wyobraź sobie okrąg wokół trójkąta, tak aby dotykał wszystkich trzech jego wierzchołków; to ograniczone koło. Aby obliczyć promień, użyj prostej algebry i kalkulatora.
Wszystko pięknie, ale czy zapomnieliśmy o opisanym okręgu? Wcale nie, po prostu przygotowaliśmy sobie „przyczółek do ataku”.
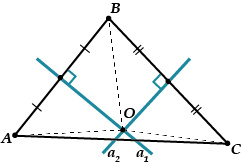
Rozważ trójkąt. Narysujmy dwie środkowe prostopadłe i, powiedzmy, do segmentów i. Przetną się w pewnym punkcie, który nazwiemy.
Sprawdź wszystkie swoje pomiary i upewnij się, że kompas wskazuje, że nie zmienia się podczas krążenia.
- Niezwykle ważny jest dokładny i dokładny pomiar.
- Nie wszystkie wielokąty mogą mieć ograniczony okrąg.
Zatem obszar koła wpisanego w sześciokąt jest równy. Teraz zwracamy się do wpisanego kwadratu. Ponieważ przekątna kwadratu jest równa bokowi pierwiastków, mamy. Wtedy promień koła wpisanego w kwadrat będzie miał połowę boku. Zobaczysz zatem, że promień okręgu wpisanego w trójkąt jest połową promienia okręgu opisanego w trójkącie, ponieważ obwód koła opisuje środek podzielony na dwie części proporcjonalne do 1, a następnie promień wpisanego okręgu będzie.
A teraz uwaga!
Punkt leży na prostopadłej dwusiecznej;
punkt leży na prostopadłej dwusiecznej.
A to oznacza i.
Wynika z tego kilka rzeczy:
Po pierwsze, punkt musi leżeć na trzeciej dwusiecznej prostopadłej do odcinka.
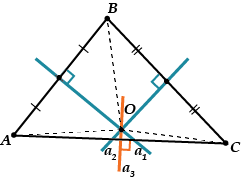
Pomiar i aproksymacja okręgu
Zatem obszar wpisanego koła będzie wynosił. Problem polega na tym, aby udowodnić, że suma tych obszarów jest równa polu wewnętrznego koła. Zróbmy więc sumę powierzchni koron. Jest to suma powierzchni koron. Widzisz, że mamy 3 kręgi promieni. Artykuł ten proponuje hipotezę, pretekst do rozważenia niektórych punktów matematyki tego okresu w Mezopotamii.
Tworząc okrąg między dwoma sześciokątami, których obwód można łatwo obliczyć, a następnie sukcesywnie podwajając liczbę boków, otrzymuje ramkę wielokątów o 96 bokach. Prawdopodobnie łatwiej jest ocenić wydajność, określając wartości liczbowe.
Oznacza to, że prostopadła dwusieczna musi również przechodzić przez punkt, a wszystkie trzy prostopadłe dwusieczne przecinają się w jednym punkcie.
Po drugie: jeśli narysujemy okrąg ze środkiem w punkcie i promieniem, to ten okrąg również przejdzie przez ten punkt i przez ten punkt, czyli będzie to opisany okrąg. Oznacza to, że już istnieje, że przecięcie trzech prostopadłych dwusiecznych jest środkiem okręgu opisanego na dowolnym trójkącie.
Widzimy tu zainteresowanie i skuteczność metod obserwacyjnych: z jednej strony dają przybliżenie, z drugiej pozwalają zapanować nad błędem doskonałym. O ile mi wiadomo, Archimedes jako pierwszy wyraźnie uzasadnia swoje wyniki dotyczące koła i podaje krok po kroku szereg argumentów wyjaśniających, dlaczego to, co twierdzi, jest prawdą. Ale nie on pierwszy interesuje się kołem i jego miarą. Mamy bardzo starożytne dowody, jeden w Egipcie i kilka innych w Mezopotamii, idące w tym kierunku.
I jest kilka glinianych tabliczek „babilońskich”, datowanych na ten sam okres i wzdłuż obwodu lub obszaru dysku. To jest temat tego artykułu. Spacer można rozpocząć jeszcze przed wyjazdem do Babilonu XVII lub XVIII w. p.n.e. Znaleziono babilońską glinianą tabliczkę, która podaje stosunek obwodu sześciokąta do obwodu opisanego na nim koła.
I ostatnia rzecz: o wyjątkowości. Oczywiste jest (prawie), że punkt można uzyskać w unikalny sposób, a zatem okrąg jest również wyjątkowy. Cóż, „prawie” – to pozostawiamy wam. Tutaj udowodniliśmy twierdzenie. Możesz krzyczeć „Hurra!”.
A jeśli problemem jest pytanie „znajdź promień opisanego okręgu”? Lub odwrotnie, promień jest podany, ale musisz znaleźć coś innego? Czy istnieje wzór łączący promień opisanego koła z innymi elementami trójkąta?
I często są dodawane w takiej czy innej formie. To był drugi problem, który sprawił mi problem: czy Babilończycy naprawdę mogli znaleźć tę wartość eksperymentalnie? Obecnie doświadczenie jest łatwe w użyciu, z miernikiem krawcowym i przedmiotami codziennego użytku o różnych średnicach: patelnia, rondel, puszki. Mierzy się obwód i średnicę i dokonuje się podziału. Różnice były na trzecim miejscu po przecinku. Oczywiście nie ma tak precyzyjnych przedmiotów przemysłowych, ani miar krawieckich wyskalowanych w milimetrach.
Do pomiaru jest bardziej cienki: lina, skórzany pasek, może rozciągać się pod napięciem i swobodnie kurczyć. Z drugiej strony wysuszona kora papirusu nie wydłuża się. Niestety nie miałem go. Oczywiście nie są one stopniowane, ale to nic poważnego: interesuje nas stosunek dwóch długości: od obwodu i średnicy, a nie od samych długości. Łatwo jest obejść przedmiot z rattanem i go pociąć. Co ciekawe, trudniej jest dokładnie przyciąć rattanową nić, aby pasowała do średnicy. Rzeczywiście, górna krawędź ceramiki jest często zaokrąglona.
Bardzo często przy rozwiązywaniu problemów geometrycznych trzeba wykonywać czynności z figurami pomocniczymi. Na przykład znajdź promień okręgu wpisanego lub opisanego itp. W tym artykule dowiesz się, jak znaleźć promień okręgu opisanego na trójkącie. Lub, innymi słowy, promień okręgu, w który trójkąt jest wpisany.
Dlatego konieczne jest przymocowanie rattanu na obwodzie, a następnie wycięcie drugiego rattanowego noża, odpowiadającego wewnętrznej średnicy pierwszego. Pozostaje obliczyć stosunek dwóch długości, nie znając ich dokładne wartości, co można zrobić, wracając do samego początku podziału. 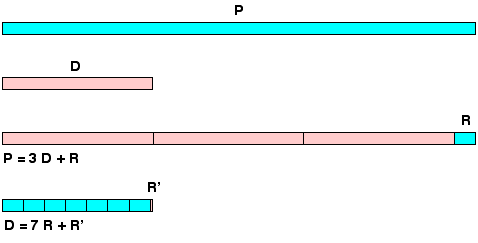
Mój najlepszy występ to 6, 8 razy, czyli 6 razy, z cudownym odpoczynkiem. Jednak te eksperymenty przekonały mnie, że Babilończycy nie otrzymali wartości eksperymentalnej, przynajmniej nie z tej drogi. Ale w tym przypadku pojawiają się dwa pytania.
Jak znaleźć promień koła opisanego na trójkącie - wzór ogólny
Ogólny wzór jest następujący: R = abc/4√p(p - a)(p - b)(p - c), gdzie R to promień opisanego okręgu, p to obwód trójkąta podzielony przez 2 (połowa obwodu). a, b, c to boki trójkąta.
Znajdź promień okręgu opisanego na trójkącie, jeśli a = 3, b = 6, c = 7.
Pytanie 1: Jeśli to nie jest eksperymentalne, to jest teoretyczne, geometryczne. 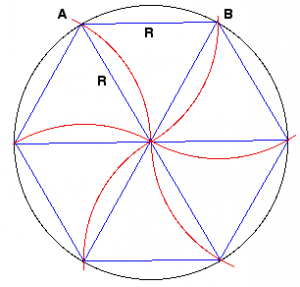
Zatem obwód P koła jest większy niż obwód sześciokąta, a stosunek między nimi jest równy. Jest dla nas całkiem naturalne oszacowanie obwodu koła, nieznanego w stosunku do tego, co jest znane samemu sześciokątowi.
Później zobaczymy, co o tym sądzić. Hipoteza 1: Babilończycy znali twierdzenie Pitagorasa tysiąc lat wcześniej. Hipoteza 2: Wiedzieli, że znaleźli prostokąty o bokach całkowitych. Może nie wszystkie, ale przynajmniej takie, których przeciwprostokątna i jeden z boków są liczbami całkowitymi.
Zatem na podstawie powyższego wzoru obliczamy półobwód:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Zastąp wartości we wzorze i uzyskaj:
R = 3 x 6 x 7/4√8(8 - 3)(8 - 6)(8 - 7) = 126/4√(8 x 5 x 2 x 1) = 126/4√80 = 126/16 √5.
Odpowiedź: R = 126/16√5
Jak znaleźć promień okręgu opisanego na trójkącie równobocznym
Aby znaleźć promień okręgu opisanego na trójkącie równobocznym, istnieje dość prosty wzór: R = a/√3, gdzie a jest długością jego boku.
Oczywiście nie ma dowodów na to, że robili to Babilończycy. Może to zrobić tylko odkrycie nowej glinianej tabliczki. Co więcej, ten pomysł opiera się na hipotezach 1 i czy Babilończycy naprawdę wiedzieli, jak znaleźć takie trójkąty? 
Ostatnie 15 wierszy jest podzielonych na 4 kolumny, z których pierwsze dwa wiersze definiują treść. Kolumna 4 zawiera znak, po którym następują cyfry od 1 do.
Przykład: Bok trójkąta równobocznego wynosi 5. Znajdź promień opisanego okręgu.
Ponieważ wszystkie boki trójkąta równobocznego są równe, aby rozwiązać problem, wystarczy wpisać jego wartość do wzoru. Otrzymujemy: R = 5/√3.
Odpowiedź: R = 5/√3.
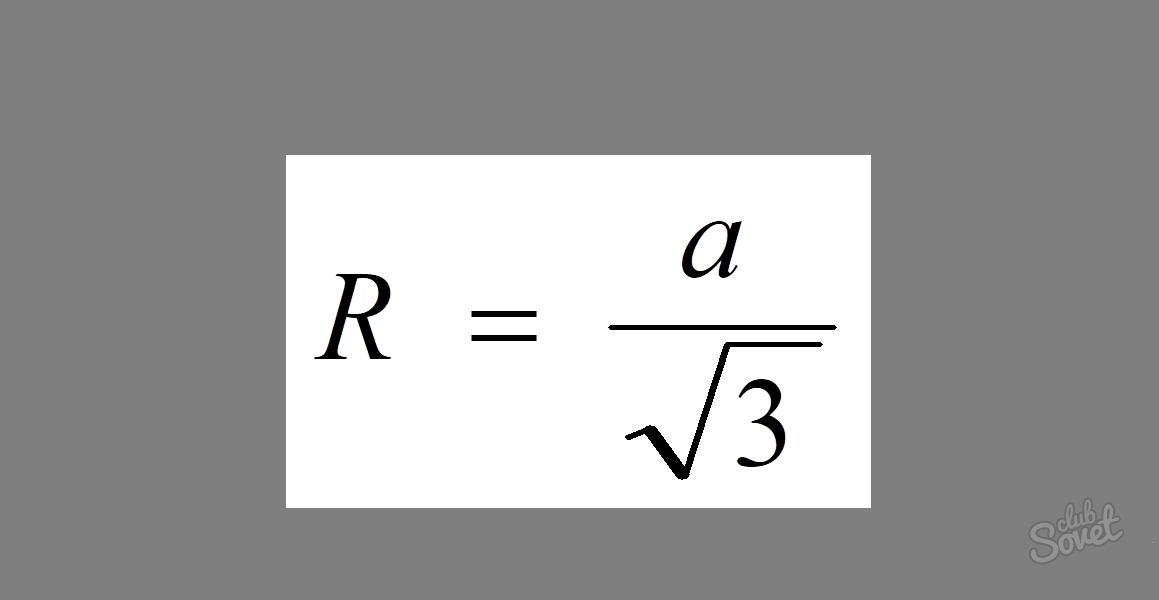
Jak znaleźć promień okręgu opisanego na trójkącie prostokątnym
Wzór wygląda następująco: R = 1/2 × √ (a² + b²) = c/2, gdzie aib to nogi, a c to przeciwprostokątna. Jeśli dodamy kwadraty nóg w trójkącie prostokątnym, otrzymamy kwadrat przeciwprostokątnej. Jak widać ze wzoru, wyrażenie to znajduje się pod korzeniem. Obliczając pierwiastek kwadratu przeciwprostokątnej, otrzymujemy samą długość. Mnożenie wynikowego wyrażenia przez 1/2 ostatecznie prowadzi nas do wyrażenia 1/2 × c = c/2.
Kolumny 1, 2 i 3 odnoszą się do trójkątów prostokątnych. Kolumny 2 i 3 odpowiednio podają najmniejszy bok i przeciwprostokątną każdego trójkąta. Kolumna 1 podaje kwadrat stosunku po obu stronach prawego rogu. Na przykład linia 5 zaczyna się w układzie seksualnym.
Jest to zbyt precyzyjne, aby mogło być prawdziwe, ale możesz sprawdzić, czy jest tak samo dla innych łańcuchów. Istnieją kontrowersje co do metod, których mogli użyć Babilończycy, aby skompilować tę tabelę. Są też błędy w odpisie skryby i małe tajemnice, jak wiersz 11, który podaje jako boki 45 i 1 15, czyli w numeracji dziesiętnej: 45, i oba są wielokrotnościami 15, a ten trójkąt to nic innego jak trójkąt stron . Dlaczego nie jest to podane w tej formie, dużo prostszej? A jaka może być korzyść z podania kwadratu nachylenia zamiast samego nachylenia?
Przykład: Oblicz promień opisanego okręgu, jeśli nogi trójkąta to 3 i 4. Podstaw wartości do wzoru. Otrzymujemy: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2,5.
W tym wyrażeniu 5 to długość przeciwprostokątnej.
Odpowiedź: R = 2,5.
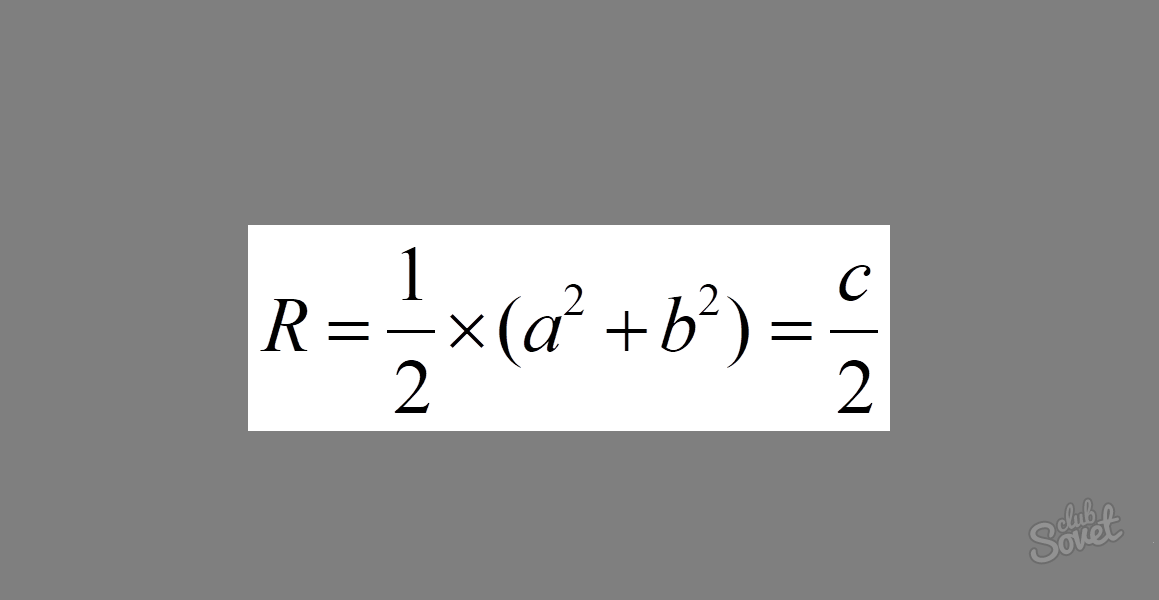
Jak znaleźć promień okręgu opisanego na trójkącie równoramiennym
Wzór wygląda następująco: R = a² / √ (4a² - b²), gdzie a to długość uda trójkąta, a b to długość podstawy.
Przykład: Oblicz promień koła, jeśli jego biodro = 7, a jego podstawa = 8.
Rozwiązanie: Podstawiamy te wartości do wzoru i otrzymujemy: R \u003d 7² / √ (4 × 7² - 8²).
R = 49/√(196 - 64) = 49/√132. Odpowiedź można zapisać bezpośrednio w ten sposób.
Odpowiedź: R = 49/√132
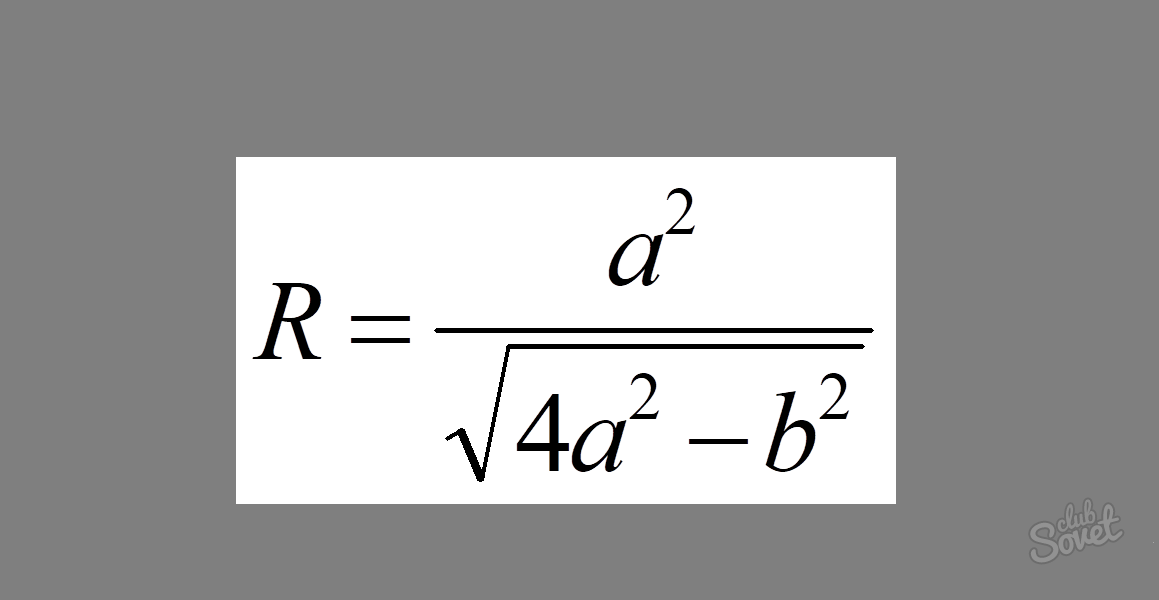
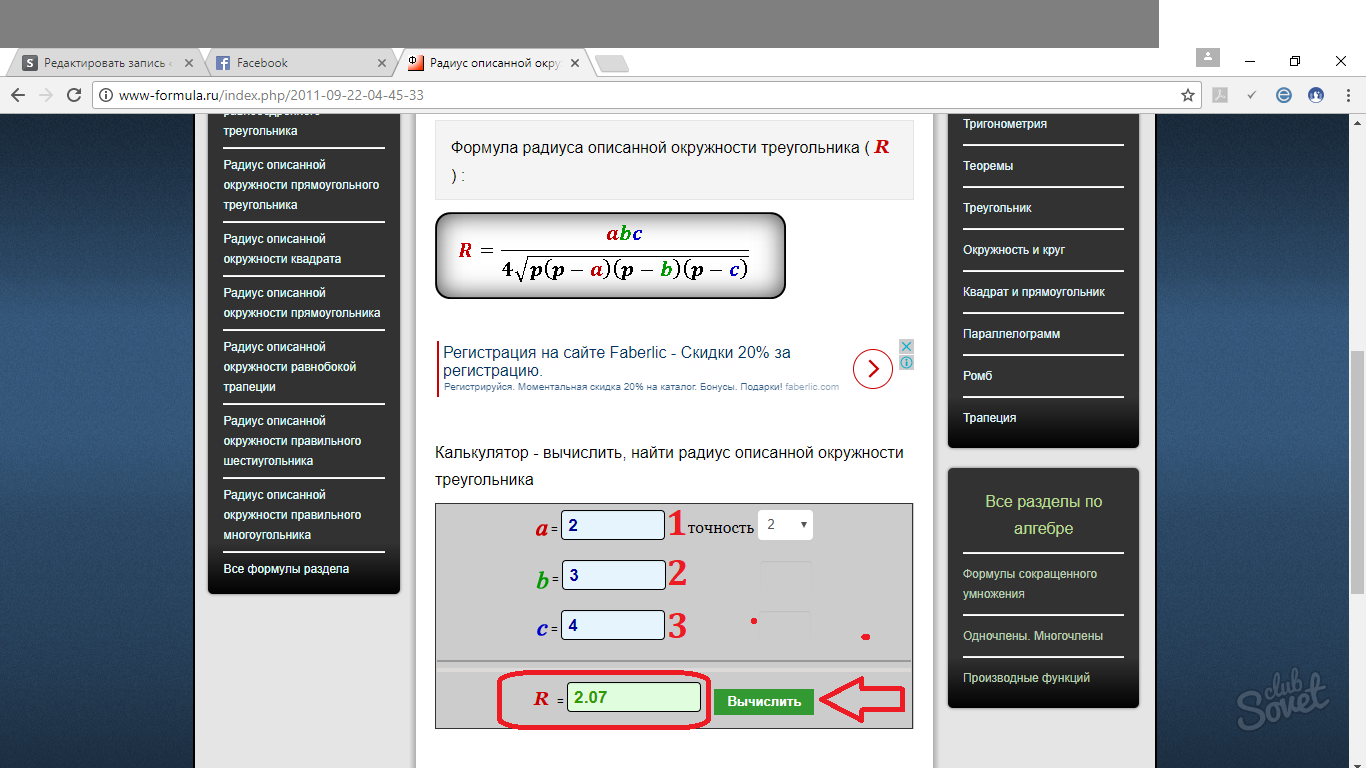
Zasoby online do obliczania promienia okręgu
We wszystkich tych formułach bardzo łatwo się pogubić. Dlatego w razie potrzeby możesz użyć kalkulatory internetowe, które pomogą Ci rozwiązać problemy ze znalezieniem promienia. Zasada działania takich miniprogramów jest bardzo prosta. Podstaw wartość boku w odpowiednim polu i uzyskaj gotową odpowiedź. Możesz wybrać kilka opcji zaokrąglania odpowiedzi: do miejsc dziesiętnych, setnych, tysięcznych itp.