Premer okroglega kroga trikotnika. Povzetek lekcije "okrožen krog". Kako najti polmer kroga, opisanega okoli trikotnika - splošna formula
V tem delu bomo razpravljali o opisanem krogu okoli (pogosto rečeno "blizu") trikotnika. Najprej dajmo definicijo.
1. Obstoj in središče opisanega kroga
Tu se pojavi vprašanje: ali takšen krog obstaja za vsak trikotnik? Izkazalo se je, da da, za vse. In poleg tega bomo zdaj oblikovali izrek, ki odgovarja tudi na vprašanje, kje je središče opisane krožnice.
Formule za iskanje dolžine diagonale pravokotnika
Formula stranice pravokotnika v premeru in kotu β. Imenuje se diagonala pravokotnika za kateri koli segment, ki povezuje dve točki nasprotnih vogalov pravokotnika. Formula za diagonalo pravokotnika glede na obe strani pravokotnika.
Formula za diagonalo pravokotnika v območju in na obeh straneh. Formula za diagonalo pravokotnika vzdolž oboda in na obeh straneh. Formula za diagonalo pravokotnika glede na polmer okroglega kroga. Formula za diagonalo pravokotnika vzdolž oboda kroga.
Poglej, takole:
Zberimo pogum in dokažimo ta izrek. Če ste že prebrali temo “”, ugotovili, zakaj se tri simetrale sekajo v eni točki, potem vam bo lažje, če pa je niste prebrali, ne skrbite: zdaj bomo ugotovili vse ven.
Dokaz bomo izvedli s konceptom geometrijskega mesta točk (LPT).
Formula za diagonalo pravokotnika glede na sinus kota, ki meji na diagonalo, in dolžino stranice nasproti tega kota. Formula za diagonalo pravokotnika v smislu kosinusa kota, ki meji na diagonalo, in dolžine stranice, ki meji na ta kot. Formula za diagonalo pravokotnika glede na sinus ostrega kota med diagonalami in površino pravokotnika.
Formule za določanje dolžine oboda pravokotnika
Obseg pravokotnika imenujemo vsota dolžin vseh stranic pravokotnika. Formula za obseg pravokotnika glede na obe strani pravokotnika. Formula za obseg pravokotnika glede na ploščino in obe strani. Formula za obseg pravokotnika vzdolž diagonale in na obeh straneh.
No, na primer, ali je množica kroglic "geometrično mesto" okroglih predmetov? Ne, seveda, ker obstajajo okrogle ... lubenice. Toda ali lahko skupina ljudi, »geometrijsko mesto«, govori? Tudi ne, ker obstajajo dojenčki, ki ne govorijo. V življenju je na splošno težko najti primer pravega "geometričnega mesta točk". Geometrija je lažja. Tukaj je na primer samo tisto, kar potrebujemo:
Formula za obseg pravokotnika glede na polmer okoli njega in na obeh straneh. Formula za obseg pravokotnika, ki je podan s premerom opisanega kroga in obeh stranic. Imenuje se območje pravokotnika v prostoru, ki ga omejujejo stranice pravokotnika, to je znotraj območja oboda pravokotnika.
Formule za določanje površine pravokotnika
Formula za površino pravokotnika z dvema stranicama. Formula za površino pravokotnika vzdolž oboda in na obeh straneh. Formula za površino pravokotnika vzdolž diagonale in na obeh straneh. Formula za površino pravokotnika vzdolž diagonale in sinusa ostrega kota med diagonalama.
Tu je niz srednja navpičnica, lastnost "" pa je "biti enako oddaljen (točka) od koncev segmenta."
Preverimo? Torej se morate prepričati o dveh stvareh:
Poveži z in z. Potem je črta sredina in višina v. Torej, - enakokraki, - smo se prepričali, da je vsaka točka, ki leži na simetrali pravokotnice, enako oddaljena od točk in.
Krog, omejen okoli pravokotnika
Formula za površino pravokotnika glede na polmer opisanega kroga in katero koli stran. Formula za območje pravokotnika v krogu je krog kroga in na obeh straneh. Imenuje se krog, omejen okoli pravokotnika, na krog, ki poteka skozi štiri oglišča pravokotnika, katerega središče je presečišče diagonal pravokotnika.
Formule za iskanje polmera kroga, urejenega okoli pravokotnika
Formula za polmer kroga, omejenega s pravokotnikom skozi dve stranici. Formula za polmer kroga, urejenega okoli pravokotnika vzdolž oboda kvadrata in obeh stranic. Formula za polmer kroga, opisanega okoli pravokotnika glede na površino pravokotnika in dolžino ene od njegovih stranic.
Vzemite - sredino in povežite in. Dobil sem mediano. Ampak - enakokraki po pogoju, ne samo mediana, ampak tudi višina, to je sredinska pravokotnica. To pomeni, da točka natančno leži na simetrali pravokotnice.
Vse! Popolnoma smo preverili dejstvo, da je pravokotna simetrala na odsek geometrijsko mesto točk, ki so enako oddaljene od koncev odseka.
Formula za polmer kroga, urejenega okoli pravokotnika vzdolž diagonale pravokotnika. Formula za polmer kroga, ki je okoli pravokotnika opisan z obodnim premerom kroga. Formula za polmer kroga, opisanega okoli pravokotnika, glede na sinus kota, ki meji na diagonalo, in dolžino stranice nasproti tega kota.
Krog, ki obdaja dani mnogokotnik, je opisan krog. Večina ljudi je že slišala za izraza obseg in polmer, omejeni krog pa je manj poznan izraz. Predstavljajte si 2D poligon z ravnimi stranicami, kot je trikotnik. Predstavljajte si krog okoli trikotnika, tako da se dotika vseh treh njegovih oglišč; to je omejen krog. Za izračun polmera uporabite preprosto algebro in kalkulator.
Vse lepo in prav, a smo pozabili na opisani krog? Sploh ne, le pripravili smo si »mosto za napad«.
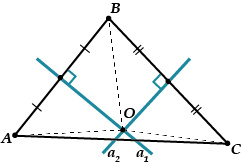
Razmislite o trikotniku. Narišimo dve sredinski navpičnici in, recimo, na segmente in. Sekala se bosta na neki točki, ki jo bomo poimenovali.
Preverite vse svoje meritve in se prepričajte, da kompas pravi, da se med vašim kroženjem ne spreminjajo.
- Izredno pomembno je natančno in natančno merjenje.
- Vsi poligoni ne morejo imeti omejenega kroga.
Tako je površina kroga, vpisanega v šesterokotnik, enaka. Zdaj se obrnemo na včrtan kvadrat. Ker je diagonala kvadrata enaka strani korena krat, imamo. Potem bo polmer kroga, včrtanega v kvadrat, imel polovico mere stranice. Tako boste videli, da je polmer kroga, včrtanega v trikotnik, polovica polmera kroga, opisanega v trikotniku, saj je obseg kroga opisan z razdeljenim medijem na dva dela, sorazmerna z 1, in nato polmer včrtanega kroga bo.
In zdaj, pozor!
Točka leži na simetrali pravokotnice;
točka leži na simetrali pravokotnice.
In to pomeni in.
Iz tega sledi več stvari:
Prvič, mora točka ležati na tretji simetrali pravokotnici na segment.
Merjenje in aproksimacija kroga
Tako bo območje včrtanega kroga. In problem je dokazati, da je vsota teh površin enaka površini notranjega kroga. Torej, naredimo vsoto površin kron. To je vsota površin kron. Vidite lahko, da imamo 3 kroge žarkov. Ta članek predlaga hipotezo, izgovor za obravnavo nekaterih točk matematike tega obdobja v Mezopotamiji.
S tem, ko med dvema šesterokotnikoma oblikuje krog, katerega obod je enostavno izračunati, nato pa zaporedno podvaja število stranic, dobi okvir s mnogokotniki s 96 stranicami. Verjetno je lažje oceniti uspešnost z navedbo številskih vrednosti.
To pomeni, da mora skozi točko potekati tudi simetrala pravokotnice in vse tri simetrale se sekajo v eni točki.
Drugič: če narišemo krog s središčem v točki in polmerom, potem bo tudi ta krog potekal skozi točko in skozi točko, to je opisani krog. To pomeni, da že obstaja, da je presečišče treh pravokotnih simetral središče opisanega kroga za vsak trikotnik.
Tu vidimo zanimivost in učinkovitost opazovalnih metod: po eni strani zagotavljajo približek, po drugi strani pa vam omogočajo nadzor popolne napake. Kolikor vem, je Arhimed prvi, ki je eksplicitno utemeljil svoje rezultate glede kroga, in podaja korak za korakom vrsto argumentov, ki pojasnjujejo, zakaj je to, kar trdi, res. Ni pa prvi, ki ga zanimata krog in njegova mera. Imamo zelo starodavne dokaze, enega v Egiptu in nekaj drugih v Mezopotamiji, ki gredo v to smer.
In obstaja nekaj "babilonskih" glinenih tablic iz istega obdobja in vzdolž oboda ali območja diska. To je tema tega članka. Sprehod se lahko začne, vendar pred odhodom v Babilon 17. ali 18. stoletje pr. Najdena je bila babilonska glinena ploščica, ki podaja razmerje med obsegom šesterokotnika in obsegom njegovega opisanega kroga.
In zadnja stvar: o edinstvenosti. Jasno (skoraj) je, da je točko mogoče dobiti na edinstven način, zato je tudi krog edinstven. No, "skoraj" - to bomo prepustili vam. Tukaj smo dokazali izrek. Lahko zavpijete "Hura!".
In če je problem vprašanje "poiščite polmer opisane kroge"? Ali obratno, radij je podan, vendar morate najti nekaj drugega? Ali obstaja formula, ki povezuje polmer opisanega kroga z drugimi elementi trikotnika?
In pogosto so dodani v takšni ali drugačni obliki. To je bil drugi, ki mi je povzročal težave: ali so Babilonci res eksperimentalno našli to vrednost? Trenutno je izkušnja enostavna za uporabo, s šiviljskim merilnikom in vsakodnevnimi predmeti različnih premerov: ponev, lonec, pločevinke. Izmeri se obseg in premer ter se naredi delitev. Razlike so bile na tretjem decimalnem mestu. Tako natančnih industrijskih predmetov seveda ni, niti šiviljskih metrov, graduiranih v milimetrih.
Za merjenje je tanjši: vrv, usnjen trak, se lahko raztegne pod napetostjo in se skrči brez težav. Po drugi strani pa se posušeno lubje papirusa ne podaljša. Na žalost ga nisem imel. Očitno niso graduirane, a to ni resno: zanima nas razmerje dveh dolžin: od oboda in premera in ne od samih dolžin. Predmet z ratanom je enostavno obiti in ga rezati. Nenavadno je, da je težje natančno odrezati nit iz ratana, da se ujema s premerom. Zgornji rob keramike je namreč pogosto zaobljen.
Zelo pogosto morate pri reševanju geometrijskih problemov izvajati dejanja s pomožnimi figurami. Na primer, poiščite polmer včrtanega ali očrtanega kroga itd. Ta članek vam bo pokazal, kako poiščete polmer kroga, ki obkroža trikotnik. Ali z drugimi besedami, polmer kroga, v katerega je vpisan trikotnik.
Zato je treba ratan pritrditi po obodu in nato odrezati drugi nož iz ratana, ki ustreza notranjemu premeru prvega. Ostaja še izračunati razmerje obeh dolžin, ne da bi ju poznali natančne vrednosti, kar lahko storimo tako, da se vrnemo k samemu izvoru delitve. 
Moj najboljši nastop je bil 6-, 8-krat, torej 6-krat, s čudovitim počitkom. Vendar so me ti poskusi prepričali, da Babilonci niso prejeli eksperimentalne vrednosti, vsaj ne na tej poti. Toda v tem primeru se postavljata dve vprašanji.
Kako najti polmer kroga, opisanega okoli trikotnika - splošna formula
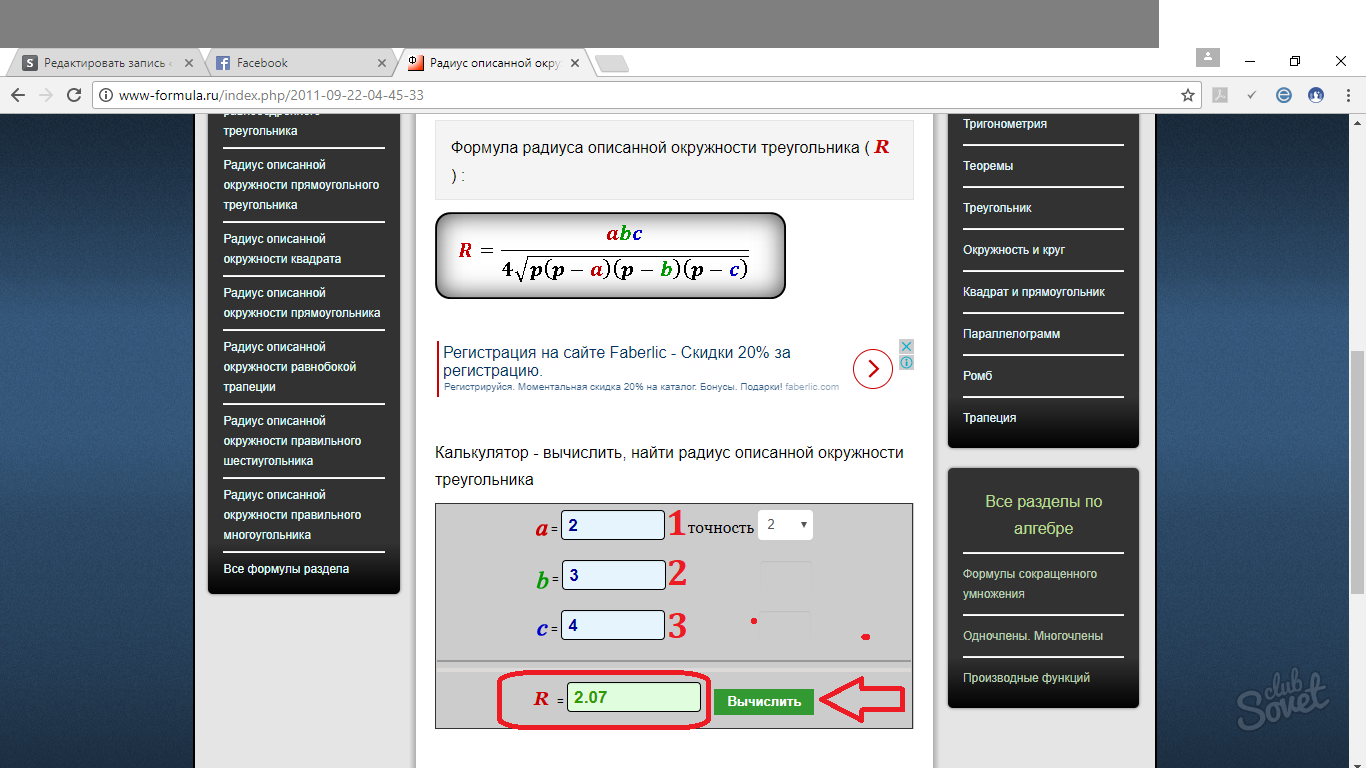
Splošna formula je naslednja: R = abc/4√p(p - a)(p - b)(p - c), kjer je R polmer opisanega kroga, p obseg trikotnika, deljen z 2 (polobod). a, b, c so stranice trikotnika.
Poiščite polmer okroglega kroga trikotnika, če je a = 3, b = 6, c = 7.
Vprašanje 1: Če ni eksperimentalno, je teoretično, geometrijsko. 
Tako je obseg P kroga večji od obsega šestkotnika, razmerje med njima pa je enako. Povsem naravno je, da ocenimo obseg kroga, ki je neznan glede na tisto, kar je znano samemu šesterokotniku.
Kasneje bomo videli, kaj si bomo o tem mislili. Hipoteza 1: Babilonci so poznali Pitagorov izrek pred tisoč leti. Hipoteza 2: Vedeli so, da so našli pravokotnike s celimi stranicami. Morda ne vsi, a vsaj tisti, katerih hipotenuza in ena od stranic sta celi števili.
Tako na podlagi zgornje formule izračunamo polobod:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Zamenjajte vrednosti v formuli in dobite:
R = 3 x 6 x 7/4√8(8 - 3)(8 - 6)(8 - 7) = 126/4√(8 x 5 x 2 x 1) = 126/4√80 = 126/16 √5.
Odgovor: R = 126/16√5
Kako najti polmer kroga, ki je opisan okoli enakostraničnega trikotnika
Če želite najti polmer kroga, opisanega okrog enakostraničnega trikotnika, obstaja dokaj preprosta formula: R = a/√3, kjer je a velikost njegove stranice.
Seveda ni dokazov, da so to storili Babilonci. To lahko stori le odkritje nove glinene tablice. Poleg tega ta ideja temelji na hipotezi 1 in ali so Babilonci res znali najti takšne trikotnike? 
Zadnjih 15 vrstic je razdeljenih v 4 stolpce, od katerih prvi dve vrstici določata vsebino. Stolpec 4 vsebuje znak, ki mu sledijo številke od 1 do.
Primer: stranica enakostraničnega trikotnika je 5. Poiščite polmer okoli njega opisanega kroga.
Ker so vse stranice enakostraničnega trikotnika enake, morate za rešitev problema samo vnesti njegovo vrednost v formulo. Dobimo: R = 5/√3.
Odgovor: R = 5/√3.
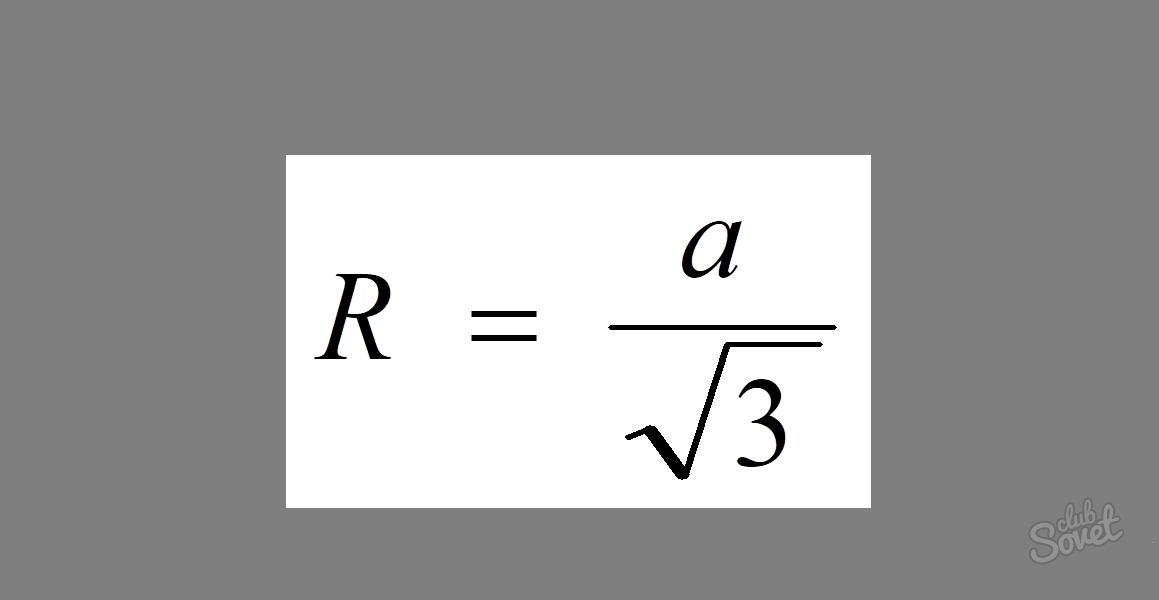
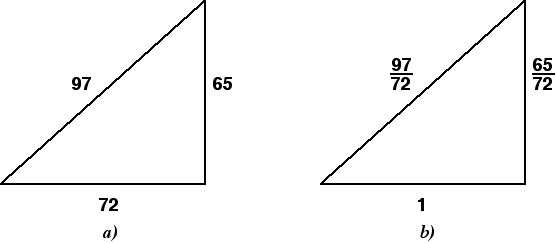
Kako najti polmer kroga, opisanega okoli pravokotnega trikotnika
Formula je videti takole: R = 1/2 × √(a² + b²) = c/2, kjer sta a in b kateta, c pa hipotenuza. Če seštejemo kvadrate katet v pravokotnem trikotniku, dobimo kvadrat hipotenuze. Kot je razvidno iz formule, je ta izraz pod korenom. Z izračunom kvadratnega korena hipotenuze dobimo samo dolžino. Množenje dobljenega izraza z 1/2 nas na koncu pripelje do izraza 1/2 × c = c/2.
Stolpci 1, 2 in 3 se nanašajo na pravokotne trikotnike. Stolpca 2 in 3 podajata najmanjšo stranico in hipotenuzo vsakega trikotnika. Stolpec 1 podaja kvadrat razmerja na obeh straneh desnega kota. Na primer, vrstica 5 se začne v spolnem sistemu.
To je preveč natančno, da bi bilo res, vendar lahko preverite, ali je enako za druge nize. Obstajajo polemike o metodah, ki so jih Babilonci morda uporabili za sestavljanje te tabele. Obstajajo tudi napake v zapisu pisarja in majhne skrivnosti, kot je 11. vrstica, ki podaja 45 in 1 15 kot strani, to je v decimalnem številčenju: 45, in oba sta večkratnika 15, in ta trikotnik ni nič drugega kot trikotnik strani. Zakaj ni podana v tej obliki, veliko preprosteje? In kakšna bi lahko bila prednost, če damo kvadrat naklona namesto samega naklona?
Primer: Izračunajte polmer opisanega kroga, če sta kraka trikotnika 3 in 4. Vrednosti nadomestite s formulo. Dobimo: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2,5.
V tem izrazu je 5 dolžina hipotenuze.
Odgovor: R = 2,5.
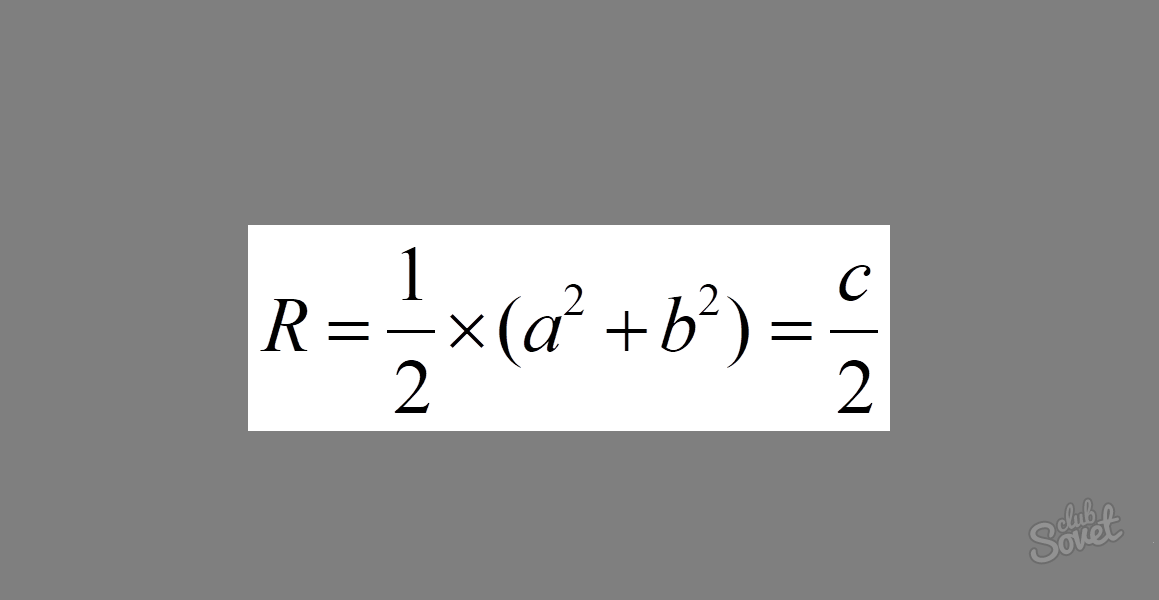
Kako najti polmer kroga, ki je opisan okoli enakokrakega trikotnika
Formula je videti takole: R = a² / √ (4a² - b²), kjer je a dolžina stegna trikotnika in b dolžina osnove.
Primer: Izračunajte polmer kroga, če je njegov steg = 7 in osnova = 8.
Rešitev: Te vrednosti nadomestimo s formulo in dobimo: R \u003d 7² / √ (4 × 7² - 8²).
R = 49/√(196 - 64) = 49/√132. Odgovor lahko zapišemo neposredno takole.
Odgovor: R = 49/√132
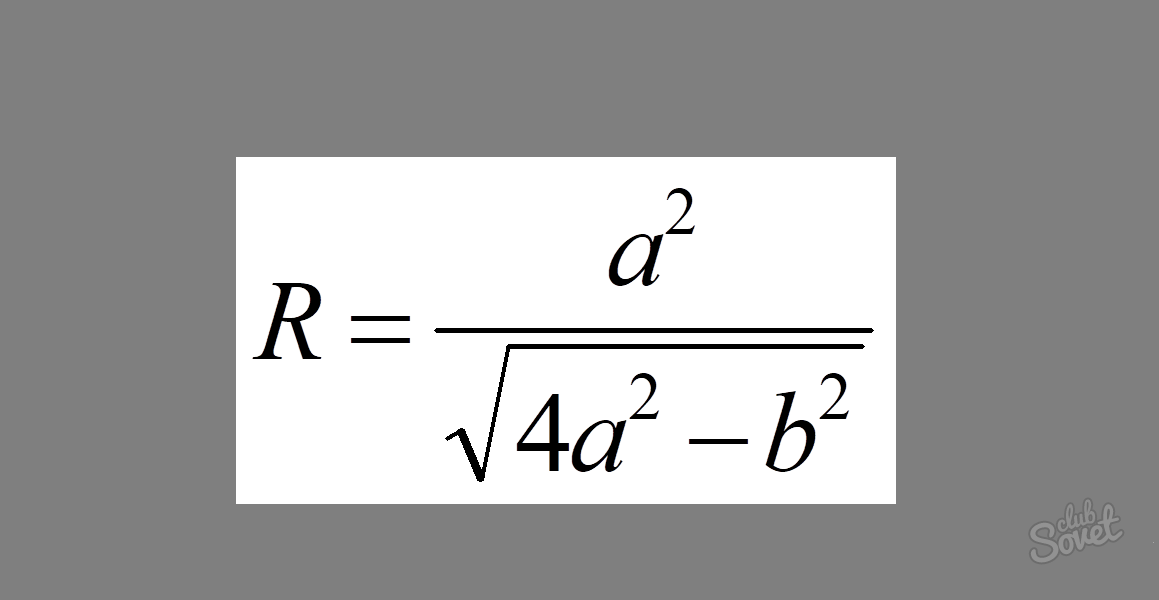
Spletni viri za izračun polmera kroga
V vseh teh formulah se je zelo enostavno zmotiti. Zato lahko po potrebi uporabite spletni kalkulatorji, ki vam bo pomagal pri reševanju nalog pri iskanju polmera. Načelo delovanja takšnih mini programov je zelo preprosto. Nadomestite vrednost strani v ustrezno polje in dobite pripravljen odgovor. Izberete lahko več možnosti zaokroževanja odgovora: na decimalke, stotinke, tisočinke itd.