Площадь многоугольника. Друзья! К вашему вниманию пару задачек с многоугольником и вписанной в него окружностью. Существует формула, которой связывается радиус указанной окружности и периметр с площадью такого многоугольника. Вот она:

Как выводится эта формула? Просто!

Имеем многоугольник и вписанную окружность. *Рассмотрим вывод на примере пятиугольника. Разобьём его на треугольники (соединим центр окружности и вершины отрезками). Получается, что у каждого треугольника основание является стороной многоугольника, а высоты образованных треугольников равны радиусу вписанной окружности:

Используя формулу площади треугольника можем записать:

Вынесем общие множители:

Уверен, сам принцип вам понятен.

*При выводе формулы количество сторон взятого многоугольника не имеет значения. В общем виде вывод формулы выглядел бы так:

*Дополнительная информация!

Известна формула радиуса окружности вписанной в треугольник

Не трудно заметить, что она исходит из полученной нами формулы, посмотрите (a,b,c – это стороны треугольника):

27640. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.

Вычисляем:

Ещё пара задач с многоугольниками.

27930. Угол между стороной правильного n -угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 54 0 . Найдите n .

Если угол между радиусом окружности и стороной многоугольника равен 54 0 , то угол между сторонами многоугольника будет равен 108 0 . Тут необходимо вспомнить формулу угла правильного многоугольника:

Остаётся подставить в формулу значение угла и вычислить n:

Всего доброго! Учитесь с удовольствием!

С уважением, Александр Крутицких.

Из жизни. В школе писали мы как-то на уроке мини-сочинение. И понадобилось мне в нем написать слово «нравится». Ну и написала я «нравица». Дома мама долго объясняла мне правило тся/ться, а я все спрашивала: «Ну почему?? Ведь говорим ЦА».
Маме надоело: «Просто запомни, когда слышится ца, пиши тся/ться». Ну ок. В следующем сочинении у меня появилась «красавится».

Как найти площадь многоугольника?

Многоугольник – это плоская или выпуклая фигура, которая состоит из пересеченных прямых (больше 3-х) и образует большое количество точек пересечения линий. Еще многоугольник можно определить как ломаную линию, которая замыкается. По-другому точки пересечения можно назвать вершинами фигуры. В зависимости от количества вершин фигура может называться пятиугольником, шестиугольником и так далее. Угол многоугольника – это угол, который образовывается сторонами, сходящимися в одной вершине. Угол находится внутри многоугольника. Причем углы могут быть разными, вплоть до 180 градусов. Есть также и внешние углы, которые обычно являются смежными внутренним.

Прямые линии, которые впоследствии пересекаются, называются сторонами многоугольника. Они могут быть соседними, смежными и не смежными. Очень важной характеристикой представленной геометрической фигуры является то, что несмежные ее стороны не пересекаются, а значит, не имеют общих точек. Смежные стороны фигуры не могут находиться на одной прямой. Те вершины фигуры, которые принадлежат одной и той же прямой, можно назвать соседними. Если провести линию между двумя вершинами, не являющимися соседними, то получится диагональ многоугольника. Что касается площади фигуры, - это внутренняя часть плоскости геометрической фигуры с большим количеством вершин, которая создается разделяющими ее отрезками многоугольника.

Как найти площадь многоугольника? Какого-либо одного решения для определения площади представленной геометрической фигуры нет, так как вариантов фигуры может быть бесконечное множество и для каждого варианта существует свое решение. Однако некоторые самые частые варианты нахождения площади фигуры все же нужно рассмотреть (они чаще всего используются на практике и включены даже в школьную программу). Прежде всего, рассмотрим правильный многоугольник, то есть такую фигуру, в которой все углы, образованные равными сторонами, являются также равными. Итак, как найти площадь многоугольника в конкретном примере? Для этого случая нахождение площади многоугольной фигуры возможно, если дан радиус окружности, вписанной в фигуру или описанной вокруг нее. Для этого можно воспользоваться следующей формулой: S = ½∙P∙r, где r – радиус окружности (вписанной или описанной), а P – является периметром геометрической многоугольной фигуры, которую можно узнать, умножив количество сторон фигуры на их длину.

Как находить площадь многоугольника

Чтобы ответить на вопрос, как находить площадь многоугольника, достаточно следовать следующему интересному свойству многоугольной фигуры, в свое время нашел известный австрийский математик – Георг Пик. Например, по формуле S = N + M/2 -1 можно найти площадь такого многоугольника, вершины которого размещены в узлах квадратной сетки. При этом S – это, соответственно, площадь; N – количество узлов квадратной сетки, которые разместились внутри фигуры с множеством углов; M – количество тех узлов квадратной сетки, которые разместились на вершинах и сторонах многоугольника. Однако, несмотря на свою красоту, формула Пика практически не применяется в практической геометрии. Как найти площадь многоугольника? Самым простым и известным методом определения площади, который изучают в школе, является разделение многоугольной геометрической фигуры на более простые части (трапеции, прямоугольники, треугольники). Найти площадь этих фигур не трудно. В этом случае площадь многоугольника определяется просто: нужно найти площади всех тех фигур, на которые разделен многоугольник. В основном определение площади многоугольника определяется в механике (размеры деталей).

Каждый, кто изучал в школе математику и геометрию, хотя бы поверхностно знает эти науки. Но со временем, если в них не практиковаться, познания забываются. Многие даже считают, что только зря потратили своё время, изучая геометрические расчёты. Однако они ошибаются. Технические работники выполняют повседневную работу, связанную с геометрическими расчётами. Что касается расчета площади многоугольника, то и эти знания находят своё применение в жизни. Понадобятся они хотя бы для того, чтобы рассчитать площадь земельного участка. Итак, давайте узнаем, как найти площадь многоугольника.

Определение многоугольника

Сначала определимся с тем, что такое многоугольник. Это плоская геометрическая фигура, которая образовалась в результате пересечения трех или более прямых. Другое простое определение: многоугольник — это замкнутая ломаная. Естественно, при пересечении прямых образуются точки пересечения, их количество равно количеству прямых, образовывающих многоугольник. Точки пересечения называют вершинами, а отрезки, образованные от прямых, - сторонами многоугольника. Смежные отрезки многоугольника находятся не на одной прямой. Отрезки, являющиеся несмежными, - это те, которые не проходят через общие точки.

Сумма площадей треугольников

Как находить площадь многоугольника? Площадь многоугольника - это внутренняя часть плоскости, которая образовалась при пересечении отрезков или сторон многоугольника. Поскольку многоугольник - это сочетание таких фигур, как треугольник, ромб, квадрат, трапеция, то универсальной формулы для вычисления его площади просто нет. На практике наиболее универсальным является метод разбиения многоугольника на более простые фигуры, нахождение площади которых не вызывают затруднений. Сложив суммы площадей этих простых фигур, получают площадь многоугольника.

Через площадь окружности

В большинстве случаев многоугольник имеет правильную форму и образует фигуру с равными сторонами и углами между ними. Рассчитать площадь в этом случае очень просто при помощи вписанной или описанной окружности. Если известна площадь окружности, то её необходимо умножить на периметр многоугольника, а затем полученное произведение поделить на 2. В итоге получается формула расчёта площади такого многоугольника: S = ½∙P∙r., где P — площадь окружности, а r — периметр многоугольника.

Метод разбиения многоугольника на «удобные» фигуры - самый популярный в геометрии, он позволяет быстро и правильно найти площадь многоугольника. 4 класс средней школы обычно изучает такие методы.

Урок из серии «Геометрические алгоритмы »

Здравствуйте, дорогой читатель.

Решения многих задач вычислительной геометрии основывается на нахождении площади многоугольника . На этом уроке мы выведем формулу для вычисления площади многоугольника через координаты его вершин, напишем функцию для вычисления этой площади.

Задача. Вычислить площадь многоугольника , заданного координатами своих вершин, в порядке их обхода по часовой стрелке.

Сведения из вычислительной геометрии

Для вывода формулы площади многоугольника нам понадобятся сведения из вычислительной геометрии, а именно, понятие ориентированной площади треугольника.

Ориентированная площадь треугольника – это обычная площадь, снабженная знаком. Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами и . То есть ее знак зависит от порядка перечисления вершин.

На рис. 1 треугольник АВС – прямоугольный. Его ориентированная площадь равна (она больше нуля, так как пара , ориентирована положительно). Эту же величину можно вычислить другим способом.

Пусть О – произвольная точка плоскости. На нашем рисунке площадь треугольника ABC получится, если из площади треугольника OBC вычесть площади OAB и OCA. Таким образом, нужно просто сложить ориентированные площади треугольников OAB, OBC и OCA. Это правило работает при любом выборе точки О .

Точно так же для вычисления площади любого многоугольника нужно сложить ориентированные площади треугольников

В сумме получится площадь многоугольника, взятая со знаком плюс, если при обходе ломаной многоугольника находится слева (обход границы против часовой стрелки), и со знаком минус, если он находится справа (обход по часовой стрелке).

Итак, вычисление площади многоугольника свелось к нахождению площади треугольника. Посмотрим, как выразить ее в координатах.

Векторное произведение двух векторов на плоскости есть площадь параллелограмма, построенного на этих векторах.

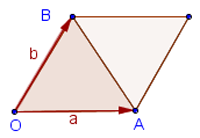
Векторное произведение, выраженное через координаты векторов:

Если координаты вершин были заданы в порядке обхода против часовой стрелки, то число S, вычисленное по этой формуле, получится положительным. В противном случае оно будет отрицательным, и для получения обычной геометрической площади нам необхо­димо взять его абсолютное значение.

Итак, рассмотрим программу для нахождения площади многоугольника, заданного координатами вершин.

Program geom6; Const n_max=200; {максимальное количество точек+1} type b=record x,y:real; end; myArray= array of b; var input:text; A:myArray; s:real; i,n:integer; procedure ZapMas(var n:integer; var A:myArray); {Заполнение массива } begin assign(input,"input.pas"); reset(input); readln(input, n); for i:=1 to n do read(input, a[i].x,a[i].y); close(input); end; function Square (A:myarray): real; {Вычисление площади многоугольника} var i:integer; S: real; begin a.x:=a.x; a.y:=a.y; s:=0; for i:=1 to n do s:= s + (a[i].x*a.y - a[i].y*a.x); s:=abs(s/2); Square:= S end; {Square} begin {main} Zapmas(n, a); PrintMas(a); S:= Square(a); writeln("S= ",s:6:2); end.

Координаты вершин считывается из файла input.pas., хранятся в массиве А в виде записей с двумя полями. Для удобства обхода многоугольника в массиве вводится n+1 элемент, значение которого равно значению первого элемента массива.

Входные данные:
5
0.6 2.1 1.8 3.6 2.2 2.3 3.6 2.4 3.1 0.5

Выходные данные:
S= 3.91

Мы решили задачу о нахождении площади многоугольника по координатам его вершин. Задачи усложняются. Если у вас есть замечания к этой статье, или пожелания, напишите в комментарии. Буду Вам очень признательна за сотрудничество.

До встречи на следующем уроке.