Диаметр описанной окружности треугольника. Конспект урока "описанная окружность". Как найти радиус окружности, описанной около треугольника — общая формула
В этой части мы обсудим окружность, описанную вокруг (часто говорят «около») треугольника. Прежде всего дадим определение.
1. Существование и центр описанной окружности
Тут возникает вопрос: а для всякого ли треугольника существует такая окружность? Вот оказывается, что да, для всякого. И более того, мы сейчас сформулируем теорему, которая ещё и отвечает на вопрос, где же находится центр описанной окружности.
Формулы для нахождения длины диагонали прямоугольника
Формула на стороне прямоугольника по диаметру и углу β. Он называется диагональю прямоугольника для любого сегмента, который соединяет две вершины противоположных углов прямоугольника. Формула диагонали прямоугольника через две стороны прямоугольника.
Формула диагонали прямоугольника по площади и с обеих сторон. Формула диагонали прямоугольника по периметру и с обеих сторон. Формула диагонали прямоугольника через радиус описанной окружности. Формула диагонали прямоугольника по окружности окружности.
Смотри, вот так:
Давай наберёмся мужества и докажем эту теорему. Если ты читал уже тему « » разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны, противоположную этому углу. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны, прилегающей к этому углу. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника.
Формулы для определения длины периметра прямоугольника
Периметр прямоугольника называется суммой длин всех сторон прямоугольника. Формула периметра прямоугольника через две стороны прямоугольника. Формула периметра прямоугольника по площади и с обеих сторон. Формула периметра прямоугольника по диагонали и с обеих сторон.
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы. А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют. В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
Формула периметра прямоугольника через радиус описанной окружности и с обеих сторон. Формула периметра прямоугольника по диаметру описанной окружности и с обеих сторон. Он называется площадью прямоугольника в пространстве, ограниченном сторонами прямоугольника, то есть внутри области периметра прямоугольника.
Формулы для определения области прямоугольника
Формула площади прямоугольника с двух сторон. Формула площади прямоугольника по периметру и с обеих сторон. Формула площади прямоугольника по диагонали и с обеих сторон. Формула площади прямоугольника по диагонали и синус острого угла между диагоналями.
Тут множество – это серединный перпендикуляр, а свойство « » - это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
Соединим с и с.Тогда линия является медианой и высотой в. Значит, – равнобедренный, – убедились, что любая точка, лежащая на серединном перпендикуляре, одинаково удалена от точек и.
Окружность, ограниченная вокруг прямоугольника
Формула площади прямоугольника по радиусу описанной окружности и любой стороны. Формула площади прямоугольника по кругу окружности окружности и с обеих сторон. Он называется окружностью, ограниченной вокруг прямоугольника, к кругу, проходящему через четыре вершины прямоугольника, центром которого является пересечение диагоналей прямоугольника.
Формулы для нахождения радиуса окружности, описанного вокруг прямоугольника
Формула радиуса круга, ограниченная прямоугольником через две стороны. Формула радиуса окружности, описанная вокруг прямоугольника по периметру квадрата и любой из сторон. Формула радиуса окружности, описанная вокруг прямоугольника через площадь прямоугольника и длину одной из ее сторон.
Возьмём – середину и соединим и. Получилась медиана. Но – равнобедренный по условию не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка - точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Формула радиуса окружности, описанная вокруг прямоугольника по диагонали прямоугольника. Формула радиуса окружности, описанная вокруг прямоугольника по окружному диаметру окружности. Формула радиуса окружности, описанная вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны, противоположную этому углу.
Кругом, окружающим данный многоугольник, является описанный круг. Большинство людей слышали термины окружность и радиус, но ограниченный круг - менее знакомый термин. Представьте себе многоугольник двумерной формы с прямыми сторонами, как треугольник. Представьте себе круг вокруг треугольника, чтобы он касался всех трех его вершин; это ограниченный круг. Чтобы вычислить свой радиус, просто используйте простую алгебру и калькулятор.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
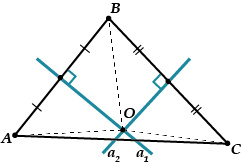
Рассмотрим треугольник. Проведём два серединных перпендикуляра и, скажем, к отрезкам и. Они пересекутся в какой-то точке, которую мы назовем.
Проверьте все ваши измерения и убедитесь, что компас говорит не меняется, пока вы кружили.
- Чрезвычайно важно точно и точно измерить.
- Не все полигоны могут иметь ограниченный круг.
Таким образом, площадь круга, вписанного в шестиугольник, равна. Теперь переходим к вписанному квадрату. Поскольку диагональ квадрата равна стороне корневых времен, мы имеем. Тогда радиус круга, вписанного в квадрат, будет иметь половину меры стороны. Таким образом, вы увидите, что радиус круга, вписанного в треугольник, составляет половину радиуса окружности, описанной в треугольнике, поскольку окружность окружности описывается разделенной средой на две части, пропорциональные 1, а затем радиус вписанной окружности будет.
А теперь, внимание!
Точка лежит на серединном перпендикуляре;
точка лежит на серединном перпендикуляре.
И значит, и.
Отсюда следует сразу несколько вещей:
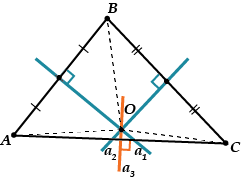
Во – первых , точка обязана лежать на третьем серединном перпендикуляре, к отрезку.
Измерение круга и приближения
Таким образом, площадь вписанного круга будет. И проблема заключается в том, чтобы доказать, что сумма этих площадей равна площади внутреннего круга. Итак, давайте сделаем сумму областей коронок. Это сумма площадей коронок. Для вас видно, что у нас есть 3 круга лучей. В этой статье предлагается гипотеза, предлог для рассмотрения некоторых пунктов математики этого периода в Месопотамии.
Образуя круг между двумя шестиугольниками, периметр которых легко подсчитывается, затем последовательно удваивая количество сторон, он получает с многоугольниками с 96 сторонами раму. Вероятно, легче оценить производительность, указав числовые значения.
То есть серединный перпендикуляр тоже обязан пройти через точку, и все три серединных перпендикуляра пересеклись в одной точке.
Во – вторых : если мы проведём окружность с центром в точке и радиусом, то эта окружность также пройдёт и через точку, и через точку, то есть будет описанной окружностью. Значит, уже есть, что пересечение трёх серединных перпендикуляров – центр описанной окружности для любого треугольника.
Мы видим здесь интерес и эффективность методов наблюдения: с одной стороны, они обеспечивают приближение, а с другой стороны, позволяют контролировать совершенную ошибку. Насколько мне известно, Архимед первым явно обосновывает свои результаты в отношении круга и дает шаг за шагом ряд аргументов, объясняющих, почему то, что он утверждает, истинно. Но он не первый, кто интересуется кругом и его мерой. У нас есть очень древние свидетельства, один в Египте и некоторые другие в Месопотамии, идущие в этом направлении.
И есть некоторые «вавилонские» глиняные таблички, относящиеся к тому же периоду и по периметру или площади диска. Это предмет этой статьи. Прогулка может начаться, но перед отъездом в Вавилон 17 или 18 веков до нашей эры. Была найдена вавилонская таблетка из глины, которая дает отношение периметра шестиугольника к периметру его ограниченного круга.
И последнее: о единственности. Ясно (почти), что точку можно получить единственным образом, поэтому и окружность – единственная. Ну, а «почти» - оставим на твоё размышление. Вот и доказали теорему. Можно кричать «Ура!».
А если в задаче стоит вопрос «найдите радиус описанной окружности»? Или наоборот, радиус дан, а требуется найти что – то другое? Есть ли формула, связывающая радиус описанной окружность с другими элементами треугольника?
И они часто добавляют в той или иной форме. Это было вторым, что вызвало у меня проблему: могли ли вавилоняне действительно найти это значение экспериментально? В настоящее время опыт прост в использовании, с метром швеи и повседневными предметами разного диаметра: сковорода, кастрюля, жестяные банки. Измеряется периметр и диаметр, и производится разделение. Различия были в третьем знаке после запятой. Конечно, нет таких точных промышленных предметов, ни метров швеи, градуированных в миллиметрах.
Для измерения он более тонкий: веревка, кожаный ремешок, могут растягиваться под напряжением и заключать контракт в покое. С другой стороны, высушенная кора папируса не удлиняется. К сожалению, у меня его не было. Очевидно, что они не градуированы, но это несерьезно: нас интересует соотношение двух длин: от периметра и диаметра, а не от самих длин. Легко обойти объект с ротаном и разрезать его. Любопытно, что менее легко точно отрезать ротанговую нить, соответствующую диаметру. Действительно, верхний край керамики часто округляется.
Очень часто при решении геометрических задач приходится совершать действия со вспомогательными фигурами. Например, находить радиус вписанной или описанной окружности и т.д. Данная статья покажет, как находить радиус окружности, описанной около треугольника. Или, иными словами, радиус окружности, в которую вписан треугольник.
Поэтому необходимо исправить ротанг по периметру, а затем разрезать второй ротанг-нож, соответствующий внутреннему диаметру первого. Остается рассчитать соотношение двух длин, не зная их точных значений, что можно сделать, вернувшись к самому происхождению деления. 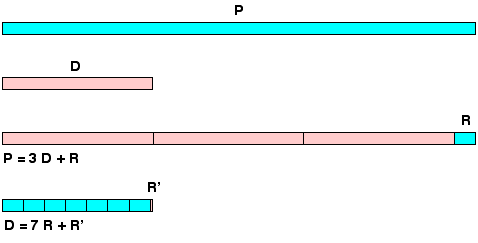
Моя лучшая производительность была в 6, 8 раз, то есть 6 раз, с замечательным отдыхом. Тем не менее, эти эксперименты убедили меня, что вавилоняне не получили экспериментальной ценности, по крайней мере, не от этого путь. Но в этом случае возникают два вопроса.
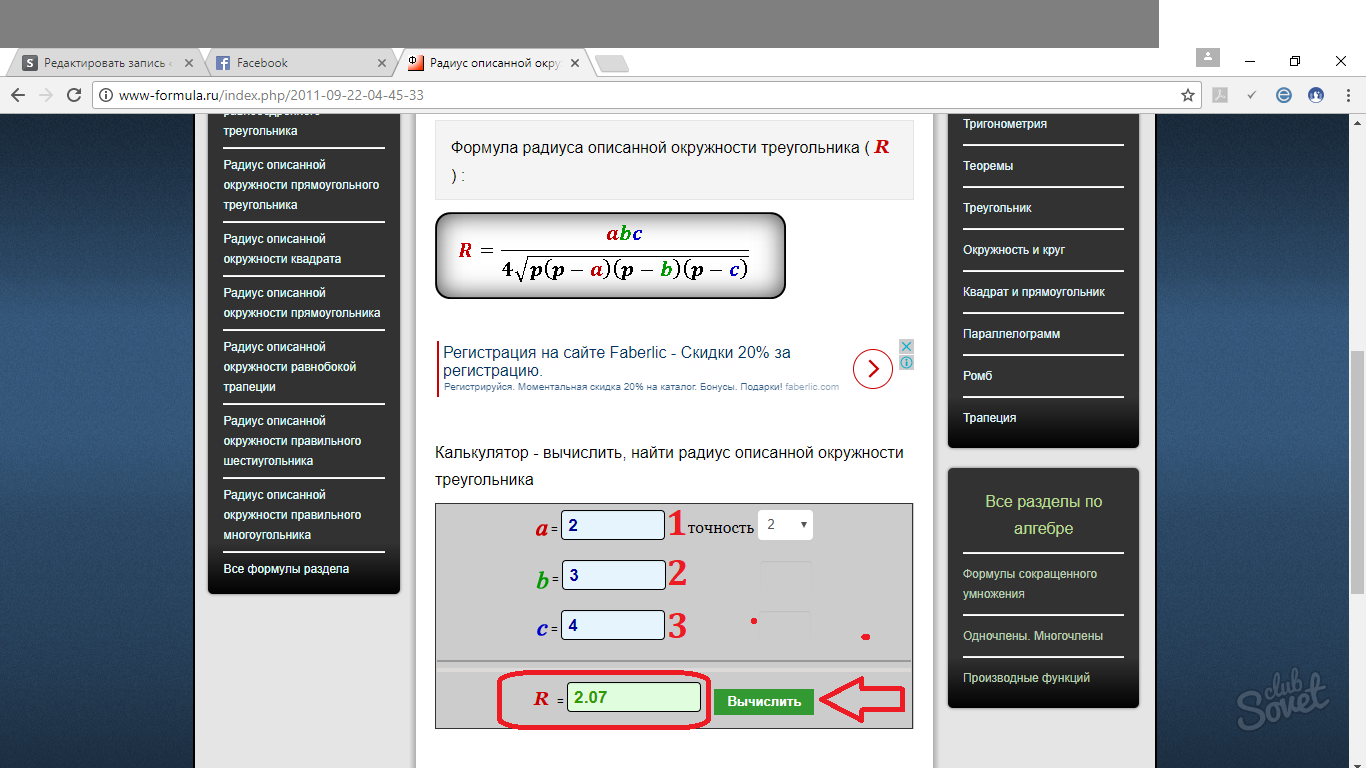
Как найти радиус окружности, описанной около треугольника — общая формула
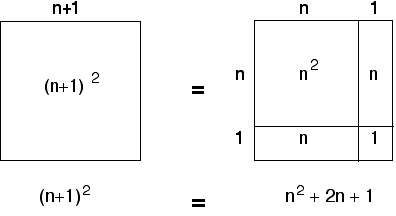
Общая формула выглядит следующим образом: R = abc/4√p(p — a)(p — b)(p — c), где R — радиус описанной окружности, p — периметр треугольника поделенный на 2 (полупериметр). a, b, c — стороны треугольника.
Найти радиус описанной окружности треугольника, если a = 3, b = 6, c = 7.
Вопрос 1: Если он не является экспериментальным, он теоретический, геометрический. 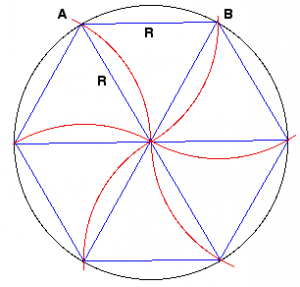
Таким образом, периметр Р окружности больше, чем у шестиугольника, и соотношение между ними равно. Для нас совершенно естественно оценить периметр круга, неизвестный по отношению к тому, что известно самому шестиугольнику.
Позже мы увидим, что об этом думать. Гипотеза 1: Вавилоняне знали теорему Пифагора за тысячу лет до этого. Гипотеза 2: они знали, что нашли прямоугольники целых сторон. Возможно, не все, но, по крайней мере, те, чья гипотенуза и одна из сторон являются целыми целыми числами.
Таким образом, исходя из вышеприведенной формулы, вычисляем полупериметр:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Подставляем значения в формулу и получаем:
R = 3 × 6 × 7/4√8(8 — 3)(8 — 6)(8 — 7) = 126/4√(8 × 5 × 2 × 1) = 126/4√80 = 126/16√5.
Ответ: R = 126/16√5
Как найти радиус окружности, описанной около равностороннего треугольника
Для нахождения радиуса окружности, описанной около равностороннего треугольника, существует довольно простая формула: R = a/√3, где a — величина его стороны.
Разумеется, нет никаких доказательств того, что вавилоняне это сделали. Только открытие новой глиняной таблетки может сделать это. Более того, эта идея основана на гипотезах 1 и действительно ли вавилоняне знали, как найти такие треугольники? 
Последние 15 строк разделены на 4 столбца, первые две строки которых определяют содержимое. Столбец 4 содержит знак, за которым следуют цифры от 1 до.
Пример: Сторона равностороннего треугольника равна 5. Найти радиус описанной окружности.
Так как у равностороннего треугольника все стороны равны, для решения задачи нужно всего лишь вписать ее значение в формулу. Получим: R = 5/√3.
Ответ: R = 5/√3.
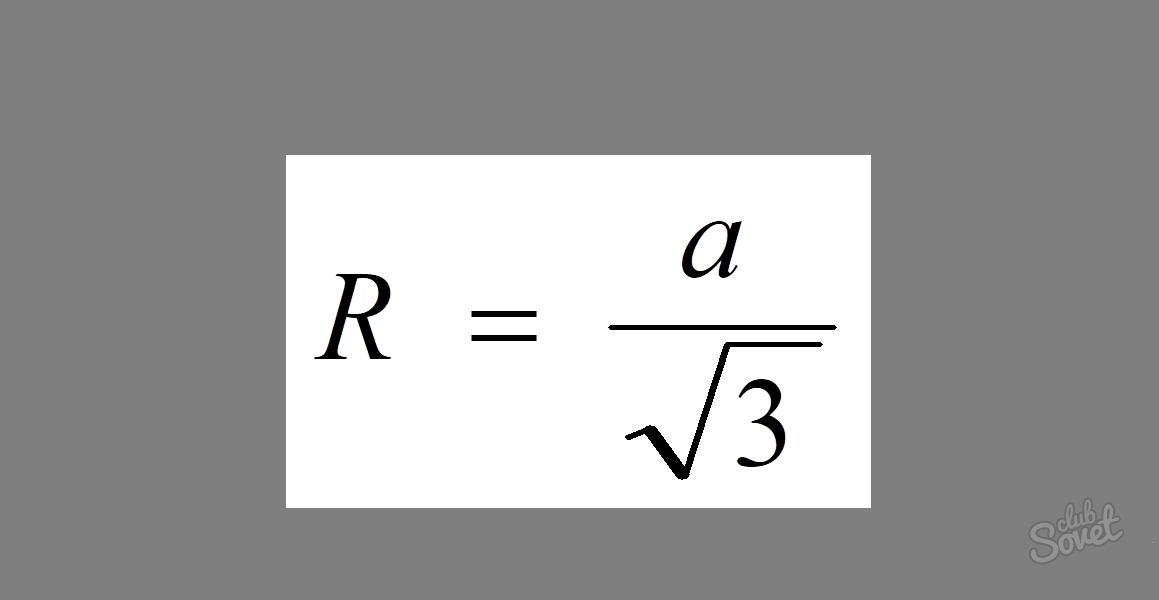
Как найти радиус окружности, описанной около прямоугольного треугольника
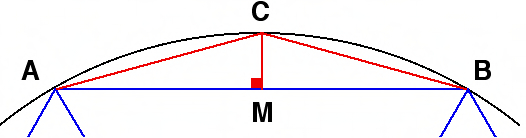
Формула выглядит следующим образом: R = 1/2 × √(a² + b²) = c/2, где a и b — катеты и c — гипотенуза. Если сложить квадраты катетов в прямоугольном треугольнике, то получим квадрат гипотенузы. Как видно из формулы, данное выражение находится под корнем. Вычислив корень из квадрата гипотенузы, мы получим саму длину. Умножение получившегося выражения на 1/2 в итоге приводит нас к выражению 1/2 × c = c/2.
Столбцы 1, 2 и 3 относятся к прямоугольным треугольникам. Столбцы 2 и 3 соответственно дают наименьшую сторону и гипотенузу каждого треугольника. Колонка 1 дает квадрат отношения по обе стороны от правого угла. Например, строка 5 начинается в сексуальной системе.
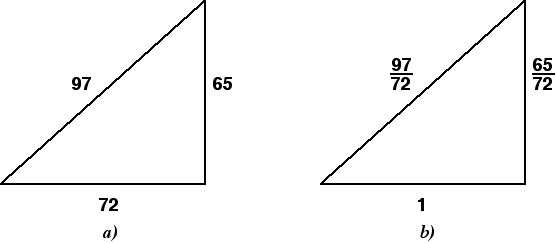
Это слишком точно, чтобы быть правдой, но вы можете проверить, что это то же самое для других строк. Существует споры о методах, которые вавилоняне могли использовать для составления этой таблицы. Также есть ошибки в копии писца и небольшие тайны, например строка 11, которая дает в качестве сторон 45 и 1 15, то есть в десятичной нумерации: 45, и оба они кратные 15, и этот треугольник - это не что иное, как треугольник сторон. Почему это не дано в этой форме, намного проще? И что может быть преимуществом, чтобы дать квадрат склона, а не самого склона?
Пример: Вычислить радиус описанной окружности, если катеты треугольника равны 3 и 4. Подставим значения в формулу. Получим: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2.5.
В данном выражение 5 — длина гипотенузы.
Ответ: R = 2.5.
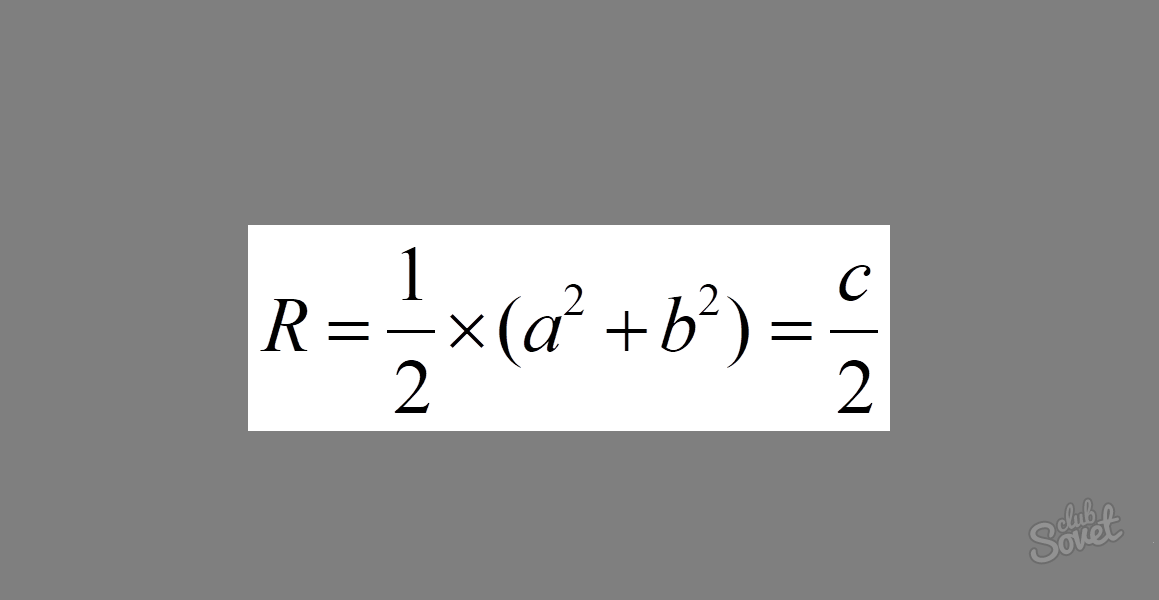
Как найти радиус окружности, описанной около равнобедренного треугольника
Формула выглядит следующим образом: R = a²/√(4a² — b²), где a — длина бедра треугольника и b — длина основания.
Пример: Вычислить радиус окружности, если его бедро = 7, а основание = 8.
Решение: Подставляем в формулу данные значения и получаем: R = 7²/√(4 × 7² — 8²).
R = 49/√(196 — 64) = 49/√132. Ответ можно записать прямо так.
Ответ: R = 49/√132
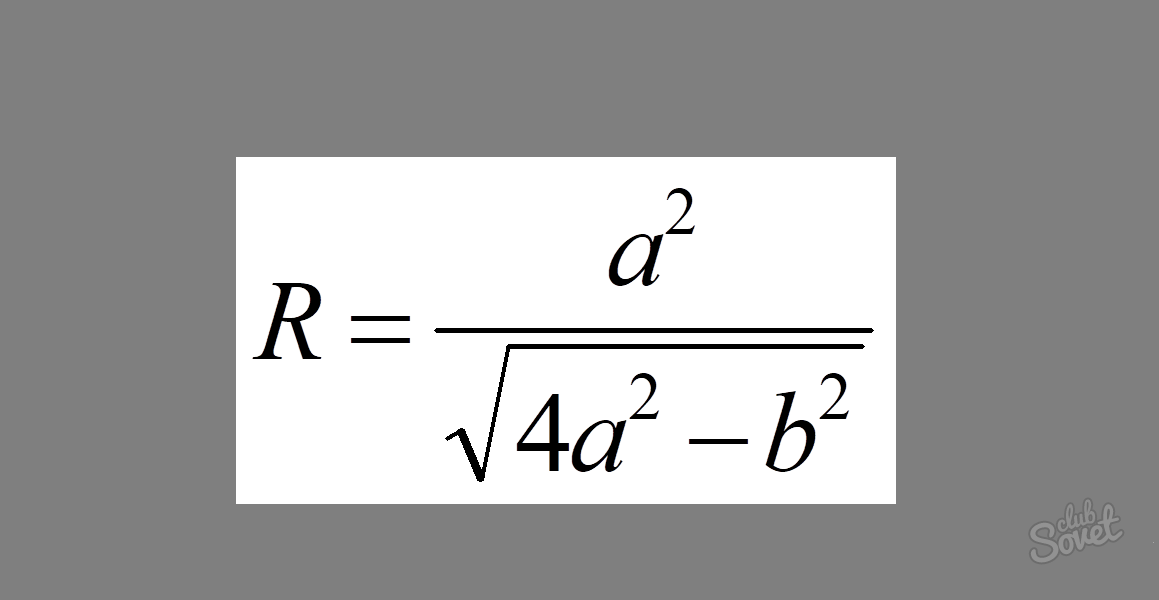
Онлайн ресурсы для вычисления радиуса окружности
Можно очень легко запутаться во всех этих формулах. Поэтому при необходимости можно воспользоваться онлайн калькуляторами, которые помогут вам в решении задач на нахождение радиуса. Принцип работы таких мини-программ очень прост. Подставляете значение стороны в соответствующее поле и получаете готовый ответ. Можно выбрать несколько вариантов округления ответа: до десятичных, сотых, тысячных и т.д.