三角形の外接円の直径。 授業「外接円」のまとめ。 三角形に外接する円の半径を求める方法 - 一般式
このパートでは、三角形の周囲の (よく「近く」と言われる) 外接円について説明します。 まず最初に、定義を与えましょう。
1. 外接円の存在と中心
ここで疑問が生じます。そのような円はどの三角形にも存在しますか? 誰にとってもそうです。 さらに、外接円の中心はどこにあるのかという質問にも答える定理を定式化します。
長方形の対角の長さを求める公式
長方形の辺の直径と角度βの公式。 長方形の対角の 2 つの頂点を結ぶ線分を長方形の対角線と呼びます。 長方形の 2 つの辺に関する長方形の対角線を求める公式。
面積と両側の長方形の対角線を求める公式。 長方形の周囲および両側の対角線を求める公式。 外接円の半径による長方形の対角線の計算式。 円の円周に沿った長方形の対角線を求める公式。
このように見える:
勇気を出してこの定理を証明してみましょう。 すでにトピック「」を読んで、3 つの二等分線が 1 つの点で交差する理由を理解している場合は、簡単に理解できるでしょう。しかし、まだ読んでいない場合でも、心配しないでください。今からすべてを理解します。
点軌跡(LPT)の概念を用いて証明を行っていきます。
対角線に隣接する角度の正弦とその角度の反対側の長さによる、長方形の対角線の公式。 対角線に隣接する角度の余弦とその角度に隣接する辺の長さによる、長方形の対角線の公式。 対角線と長方形の面積の間の鋭角の正弦を表す、長方形の対角線の公式。
長方形の周囲の長さを求める公式
長方形の周囲長は、長方形のすべての辺の長さの合計と呼ばれます。 長方形の 2 辺を基準とした長方形の周囲の長さを求める公式。 面積と両辺を指定して、長方形の周囲長を求める公式。 長方形の対角線と両側の周囲長を求める公式。
たとえば、ボールの集合は丸いオブジェクトの「幾何学的な場所」でしょうか? いや、もちろん、丸い…スイカがあるから。 しかし、人々の集合体、つまり「幾何学的な場所」は話すことができるのでしょうか? 話せない赤ちゃんもいるからです。 生活の中で、実際の「点の幾何学的な場所」の例を見つけることは一般に困難です。 幾何学は簡単です。 たとえば、必要なものは次のとおりです。
長方形の外周とその両側の半径を求める公式。 外接円と両辺の直径から長方形の周囲長を求める公式。 長方形の辺で囲まれた空間、つまり長方形の周囲領域の内側の長方形の面積と呼ばれます。
長方形の面積を求める公式
2つの辺を持つ長方形の面積を求める公式。 長方形の周囲と両側の面積を求める公式。 長方形の対角線と両側の面積を求める公式。 対角線に沿った長方形の面積と対角線の間の鋭角の正弦を求める公式。
ここで集合は中央の垂線であり、プロパティ「」は「線分の端から等距離(点)にある」です。
確認しよう? したがって、次の 2 つのことを確認する必要があります。
と を接続すると、線は中央値と高さになります。 したがって、 - 二等辺線 - 垂直二等分線上にある点がそれらの点から等距離にあることを確認しました。
長方形の周囲に囲まれた円
外接円の半径と任意の辺を指定して長方形の面積を求める公式。 円の中の長方形の面積の公式は、円の両側の円です。 長方形の4つの頂点を通り、その中心が長方形の対角線の交点である円を、長方形の外周円と呼びます。
長方形に外接する円の半径を求める公式
2 辺を通る長方形で囲まれた円の半径を求める公式。 正方形の周囲と各辺に沿って長方形に外接する円の半径を求める公式。 長方形の周囲の円の半径を長方形の面積とその辺の長さで表す公式。
~真ん中を取って接続して。 中央値を取得しました。 ただし、条件による二等辺、中央値だけでなく、高さ、つまり中央値の垂線も異なります。 これは、点が正確に垂直二等分線上にあることを意味します。
全て! 線分の垂直二等分線が線分の端から等距離にある点の軌跡であるという事実を十分に検証しました。
長方形の対角線に沿って長方形に外接する円の半径を求める公式。 円の半径を長方形の周囲に円の周径で表す公式。 円の半径の公式は、対角線に隣接する角度の正弦と、この角度の反対側の長さによって長方形の周囲で記述されます。
与えられた多角形を囲む円が外接円です。 ほとんどの人は円周と半径という用語を聞いたことがあるでしょうが、有界円はあまり馴染みのない用語です。 三角形のような直線の辺を持つ 2D 多角形を想像してください。 三角形の 3 つの頂点すべてに接するように、三角形の周りを円で囲むと想像してください。 限定サークルです。 半径を計算するには、簡単な代数と計算機を使用するだけです。
それはそれでいいのですが、外接円のことを忘れてしまったのでしょうか? そんなことはなく、単に「攻撃の橋頭堡」を用意しただけなのです。
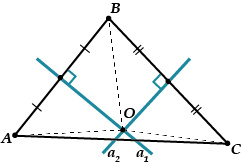
三角形を考えてみましょう。 たとえば、セグメントに対して 2 つの中央の垂線を引いてみましょう。 それらはある時点で交差しますが、その点に名前を付けます。
すべての測定値をチェックし、旋回中にコンパスが変化しないことを示していることを確認してください。
- 正確かつ正確に測定することが非常に重要です。
- すべてのポリゴンが有界円を持つことができるわけではありません。
したがって、六角形に内接する円の面積は に等しい。 次に、内接正方形に目を向けます。 正方形の対角線は根の辺に等しいので、次のようになります。 すると、正方形に内接する円の半径は辺の半分の長さになります。 したがって、三角形に内接する円の半径は、三角形に外接する円の半径の半分であることがわかります。これは、円の円周が 1 に比例して 2 つの部分に分割された媒質によって記述されるため、内接円の半径は次のようになります。
そして今、注目してください!
点は垂直二等分線上にあります。
点は垂直二等分線上にあります。
そしてそれはそしてという意味です。
これからいくつかのことがわかります。
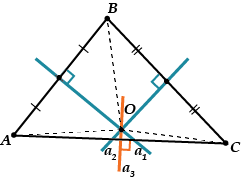
まず最初に、点はセグメントの 3 番目の垂直二等分線上になければなりません。
円の測定と近似
したがって、内接円の面積は となります。 そして問題は、これらの面積の合計が内円の面積に等しいことを証明することです。 それでは、クラウンの面積の合計を計算してみましょう。 これはクラウンの面積の合計です。 光線の円が 3 つあることがわかります。 この記事は、メソポタミアのこの時代の数学のいくつかの点を検討するための口実である仮説を提案します。
2 つの六角形の間に円を形成し、その周長は簡単に計算でき、その後、辺の数を連続的に 2 倍にすることで、96 辺の多角形からなるフレームが得られます。 おそらく数値を指定してパフォーマンスを評価する方が簡単です。
つまり、垂直二等分線もその点を通過する必要があり、3 つの垂直二等分線はすべて 1 点で交差します。
第二に: 点を中心とし、半径を持つ円を描くと、この円は点と点を通過します。つまり、外接円になります。 これは、どの三角形でも 3 つの垂直二等分線の交点が外接円の中心となることがすでに存在することを意味します。
ここで、観察手法の興味と有効性が分かります。観察手法は、一方では近似値を提供し、他方では完全な間違いを制御できるようにします。 私の知る限り、アルキメデスは円に関する自身の結果を明確に正当化した最初の人物であり、彼の主張がなぜ真実であるかを説明する一連の議論を段階的に示しています。 しかし、円とその尺度に興味を持ったのは彼が初めてではない。 非常に古い証拠があり、その方向に進む証拠はエジプトにあり、メソポタミアにもあります。
そして、円盤の周囲または領域に沿って、同じ時代の「バビロニア」粘土板がいくつかあります。 これがこの記事の主題です。 紀元前 17 世紀または 18 世紀のバビロンに出発する前であれば、散歩を始めることもできます。 バビロニアの粘土板が発見されており、六角形の周囲長とその外接円の周囲長の比が示されています。
そして最後は、独自性についてです。 ポイントが一意の方法で取得できることは (ほぼ) 明らかであり、したがって円も一意です。 まあ、「ほぼ」、それはあなたにお任せします。 ここで定理を証明しました。 「万歳!」と叫ぶことができます。
では、問題が「外接円の半径を求めよ」だとしたら? またはその逆、半径は指定されていますが、何か他のものを見つける必要があるでしょうか? 外接円の半径と三角形の他の要素を関係付ける公式はありますか?
そして、それらはしばしば何らかの形で追加されます。 これは私に問題を引き起こした 2 番目のものでした。バビロニア人は本当にこの値を実験的に見つけることができたのでしょうか? 現在、この体験は裁縫メーターと、フライパン、鍋、ブリキ缶などのさまざまな直径の日用品を使用して、簡単に使用できます。 外周と直径を測定し、分割します。 違いは小数点以下第 3 位でした。 もちろん、そんな精密な工業製品はありませんし、お針子が使うミリ単位のメーターもありません。
測定の場合は、ロープや革紐など、より細いものを使用します。張力下では伸び、簡単に縮むことができます。 一方、乾燥したパピルスの樹皮は伸びません。 残念ながら、持っていませんでした。 明らかに、それらは目盛り付きではありませんが、これは深刻ではありません。私たちは、長さそのものではなく、周囲と直径による 2 つの長さの比に興味があるのです。 籐で物をぐるぐる回してカットするのは簡単です。 不思議なことに、直径に合わせて籐糸を正確に切断するのはそれほど簡単ではありません。 実際、土器の上端は丸みを帯びていることが多いです。
幾何学的な問題を解くときは、補助図形を使用してアクションを実行する必要があることがよくあります。 たとえば、内接円や外接円の半径などを求めます。 この記事では、三角形に外接する円の半径を求める方法を説明します。 言い換えれば、三角形が内接する円の半径です。
したがって、籐の周囲を固定し、最初の籐ナイフの内径に対応して 2 番目の籐ナイフを切断する必要があります。 2つの長さを知らずに、2つの長さの比率を計算する必要があります 正確な値、それは割り算の原点に立ち返ることによって可能になります。 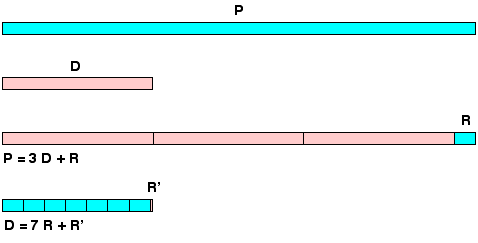
私の最高のパフォーマンスは6、8回、つまり素晴らしい休息を挟んだ6回でした。 しかし、これらの実験は、バビロニア人が、少なくともこのルートからは実験的価値を受け取らなかったことを私に確信させました。 しかしこの場合、2つの疑問が生じます。
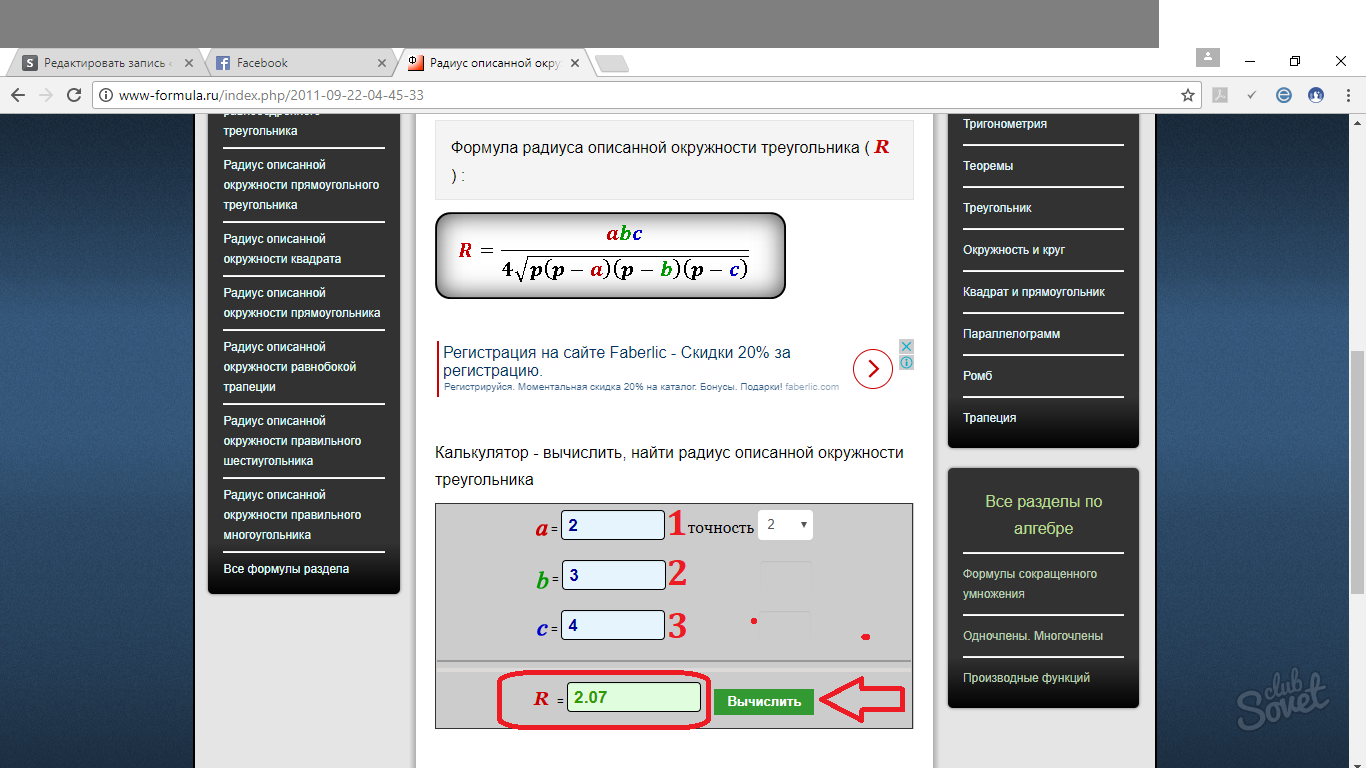
三角形に外接する円の半径を求める方法 - 一般式
一般式は次のとおりです: R = abc/4√p(p - a)(p - b)(p - c)、ここで R は外接円の半径、p は三角形の周囲長を 2 (半周長) で割ったものです。 a、b、c は三角形の辺です。
a = 3、b = 6、c = 7の場合の三角形の外接円の半径を求めます。
質問 1: 実験的でない場合、それは理論的、幾何学的です。 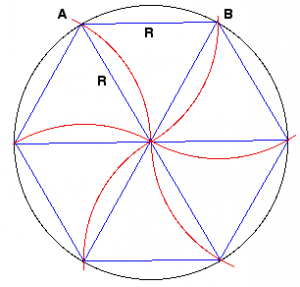
したがって、円の周長 P は六角形の周長よりも大きく、それらの比は等しいです。 六角形自体の既知の範囲に比べて未知の円の周囲を推定することは、私たちにとって極めて自然なことです。
それについてどう考えるべきかは後ほど見ていきます。 仮説 1: バビロニア人は千年前にピタゴラスの定理を知っていました。 仮説 2: 彼らは、辺が整数の長方形を見つけたことを知っていました。 すべてではないかもしれませんが、少なくとも斜辺と辺の 1 つが整数であるものは含まれます。
したがって、上記の式に基づいて、半周長を計算します。
p = (a + b + c)/2 = 3 + 6 + 7 = 16。 => 16/2 = 8。
数式の値を代入すると、次のようになります。
R = 3 × 6 × 7/4√8(8 - 3)(8 - 6)(8 - 7) = 126/4√(8 × 5 × 2 × 1) = 126/4√80 = 126/16√5。
答え: R = 126/16√5
正三角形に外接する円の半径を求める方法
正三角形に外接する円の半径を求めるには、R = a/√3 という非常に単純な公式があります。ここで、a はその辺のサイズです。
もちろん、バビロニア人がこれを行ったという証拠はありません。 新しい粘土板の発見だけがこれを可能にします。 さらに、この考えは仮説 1 に基づいていますが、バビロニア人は本当にそのような三角形の見つけ方を知っていたのでしょうか? 
最後の 15 行は 4 つの列に分割されており、最初の 2 行で内容が定義されます。 列 4 には、符号の後に 1 から 1 までの数字が含まれます。
例:正三角形の辺は5です。外接円の半径を求めます。
正三角形のすべての辺は等しいため、問題を解決するには、その値を数式に入力するだけで済みます。 R = 5/√3 が得られます。
答え: R = 5/√3。
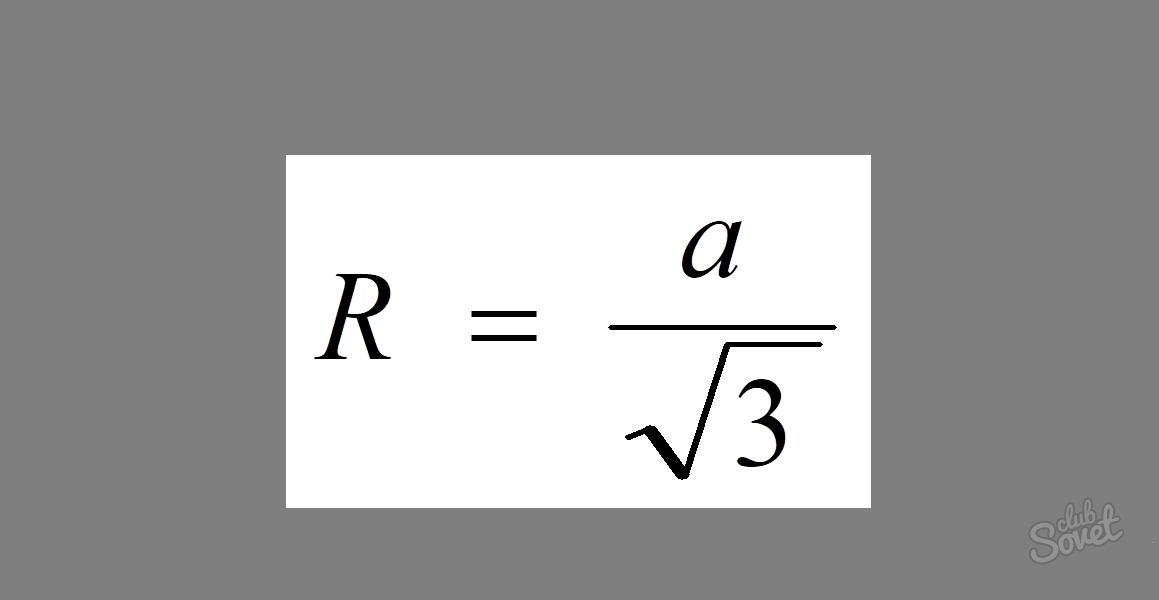
直角三角形に外接する円の半径を求める方法
式は次のようになります。 R = 1/2 × √(a² + b²) = c/2、ここで、a と b は脚、c は斜辺です。 直角三角形の足の二乗を加算すると、斜辺の二乗が得られます。 式からわかるように、この式はルートの下にあります。 斜辺の二乗根を計算することで、長さ自体が得られます。 結果の式に 1/2 を乗算すると、最終的に 1/2 × c = c/2 という式が得られます。
列 1、2、および 3 は直角三角形を指します。 列 2 と列 3 はそれぞれ、各三角形の最小辺と斜辺を示します。 列 1 は、右隅の両側の比率の 2 乗を示します。 たとえば、5 行目は性的システムで始まります。
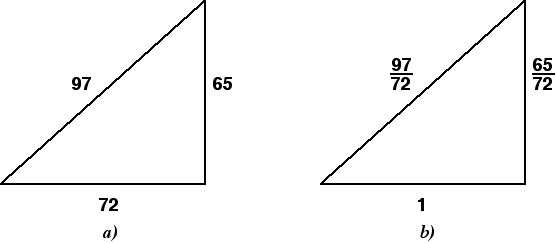
これは正確すぎるため真実ではありませんが、他の文字列でも同じであることを確認できます。 バビロニア人がこの表を作成するために使用した可能性のある方法については議論があります。 また、筆記者の写しには誤りがあり、辺として 45 と 1 15 を与える 11 行目、つまり 10 進数で 45 を与えており、両方とも 15 の倍数であり、この三角形は辺の三角形にすぎません。 なぜもっと単純なこの形式で与えられないのでしょうか? そして、勾配そのものではなく、勾配の 2 乗を与えることにどのような利点があるでしょうか?
例:三角形の足が3本と4本の場合の外接円の半径を計算します。数値を式に代入します。 R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2.5 が得られます。
この式では、5 は斜辺の長さです。
答え: R = 2.5。
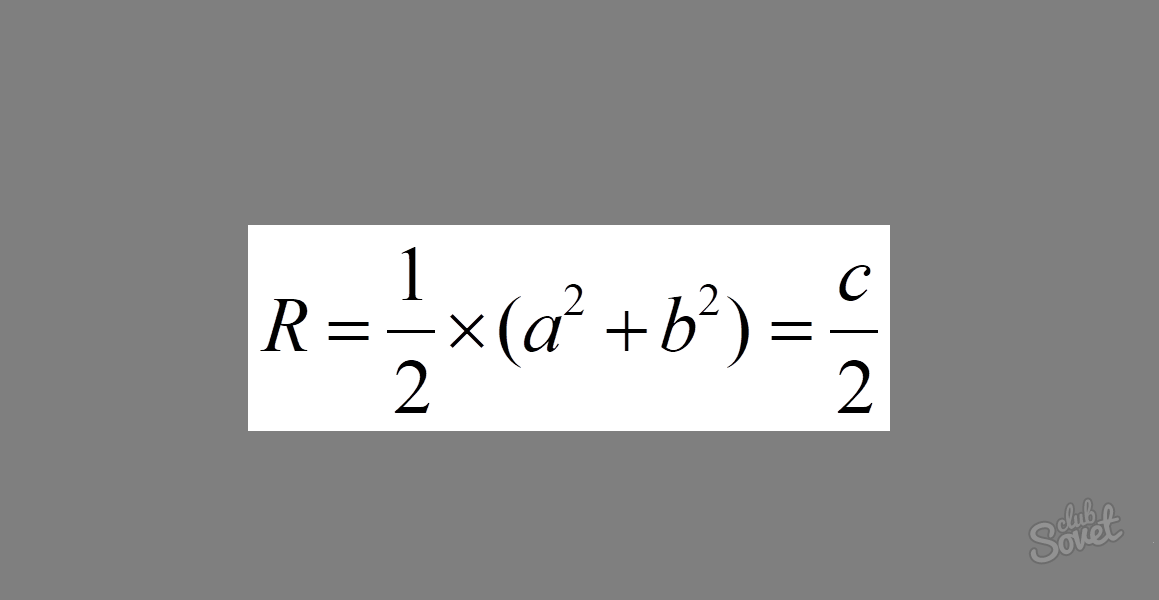
二等辺三角形に外接する円の半径を求める方法
式は次のようになります: R = a² / √ (4a² - b²)。ここで、a は三角形の太ももの長さ、b は底辺の長さです。
例: ヒップ = 7、底辺 = 8 の場合、円の半径を計算します。
解決策: これらの値を式に代入して、R \u003d 7² / √ (4 × 7² - 8²) を取得します。
R = 49/√(196 - 64) = 49/√132。 答えはこのように直接書くことができます。
答え: R = 49/√132
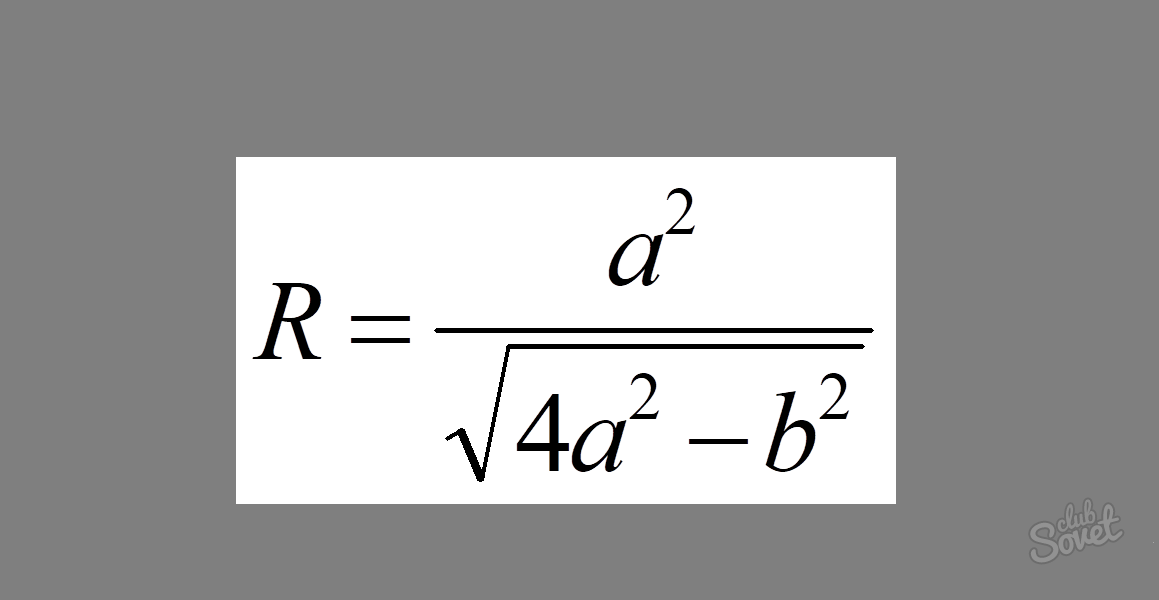
円の半径を計算するためのオンライン リソース
これらすべての公式は非常に混乱しやすいです。 したがって、必要に応じて、次を使用できます。 オンライン計算機、半径を求める問題を解決するのに役立ちます。 このようなミニプログラムの動作原理は非常に簡単です。 辺の値を適切なフィールドに置き換えると、既製の答えが得られます。 答えを四捨五入するためのいくつかのオプション (小数点、100 分の 1、1000 分の 1 など) を選択できます。