Свойство хорды перпендикулярной диаметру. Секущие и хорды в окружности. Средний уровень. Свойства хорд и касательных
Хорда – это отрезок, который соединяет две произвольные точки одной окружности. Нахождение длины данного элемента окружности – это задача, относящаяся к геометрическому разделу математики. Для ее вычисления необходимо сделать упор на величины, данные в задаче, а также свойства других элементов.
Существует несколько типов задач на нахождение хорды. В каждом из них даны различные значения, которые могут быть использованы для проведения необходимых вычислений.
На следующих диаграммах приводится краткое изложение некоторых теорем аккорда: перпендикулярная биссектриса и конгруэнтные аккорды. Прокрутите страницу вниз для примеров, объяснений и решений. Хорда - это прямая линия, соединяющая 2 точки по окружности круга.
Теорема. Радиус или диаметр, перпендикулярный хорде, делит хорду на две равные части и наоборот. Конверс: перпендикулярный биссектр хорды проходит через центр круга. Если две хорды в круге конгруэнтны, то их перехваченные дуги конгруэнтны. Конверс: если две дуги конгруэнтны, то соответствующие им хорды конгруэнтны.
Как найти хорду окружности — случай 1
Задается окружность, в которой есть радиус R. Если дуга φ стягивается хордой L, при этом φ задана в градусах, то значение длины хорды будет вычисляться следующим образом: L = 2*R*sin(φ/2). Для решения задачи необходимо будет просто подставить числовые значения и вычислить.
Как найти хорду окружности — случай 2
- Задается окружность, центр которой лежит в т. О и хордами АВ и АС, которые пересекают окружность в общей т. А. В этом случае угол, который образуют хорды (ВАС), опирается на диаметр. В данном случае рекомендуется выполнить пояснительный чертеж, чтобы было видно образование равнобедренного треугольника АВС, в котором ВС – основание и диаметр, следовательно, ВО=ОС (как радиусы). Тогда АО является медианой в треугольнике и еще одним радиусом. АВ и АС – стороны треугольника, АВ=АС (т.к. треугольник является равнобедренным). Треугольники АОС и АОВ являются прямоугольными и равнобедренными. Зная радиус, по теореме Пифагора вычисляется хорда: АС 2 =АО 2 +ОС 2 .
- В данном случае можно воспользоваться другой формулой, если известен диаметр и центральный угол, на который опирается хорда: L = 2R*Sin (α/2) = D*Sin (α/2).

Окружность и круг. Основные понятия и свойства
В этом видео обсуждаются следующие теоремы. Конгруэнтные центральные углы имеют конгруэнтные аккорды. Конгруэнтные аккорды имеют конгруэнтные дуги. Конгруэнтные дуги имеют конгруэнтные центральные углы. Это видео описывает четыре свойства аккордов. Если два хорды в круге конгруэнтны, то они определяют два центральных угла, которые являются конгруэнтными. Если два хорды в круге конгруэнтны, то их перехваченные дуги конгруэнтны. Если две хорды в круге конгруэнтны, то они равноудалены от центра круга.
Как найти хорду окружности — случай 3
Когда задается окружность с диаметром и хордой и дается угол между ними (α), то необходимо провести перпендикуляр к центру с другой точки пресечения хордой окружности. Получится прямоугольный треугольник. Теорема о проекциях позволяет вывести формулу, которую можно использовать для нахождения хорды: СЕ = 2* R *cos α.
Перпендикуляр от центра круга до аккорда делит пополам аккорд. Попробуйте приведенные примеры или введите свою собственную проблему и проверьте свой ответ с пошаговыми объяснениями. Рисунок 1 Круг с четырьмя радиусами и двумя аккордами. Теорема 78: В круге, если две хорды равны по мере, то соответствующие младшие дуги равны по мере.
Обратное утверждение этой теоремы также верно. Теорема 79: в круге, если две мерительные дуги равны по мере, то их соответствующие хорды равны по мере. Рисунок 2 Связь между равенством мер аккордов и равенством мер их соответствующих второстепенных дуг.

Как найти хорду окружности — полезные свойства
- Хорда, проходящая через центр заданной окружности, будет являться ее диаметром.
- Если в окружности проведено две хорды, которые пересекаются между собой, то срабатывает такое свойство: угол между ними будет равен ½ суммы мер двух дуг: расположенной напротив хорды и той, что находится в углу.
- В случае, когда к заданной окружности проводится касательная, которая образует с хордой угол, то он будет равен значению, полученному в результате деления величины дуги, которую стягивает данная хорда, на 2.
Часть 3. Окружности
Ниже приведены некоторые дополнительные теоремы о аккордах в круге без объяснения причин. Эти теоремы могут быть использованы для решения многих проблем. Теорема 80: если диаметр перпендикулярен хорде, то он делит пополам хорду и ее дуги. Рисунок 3 Диаметр, перпендикулярный хорде.
Теорема 81: в круге, если две хорды равны по мере, то они равноудалены от центра. Рисунок 4 В круге соотношение между двумя аккордами равномерно и равноудалено от центра. Теорема 82: в круге, если две хорды равноудалены от центра круга, то эти два аккорда равны по мере.
I . Справочные материалы.
I . Свойства касательных, хорд и секущих. Вписанные и центральные углы.
Окружность и круг
1.Если из одной точки, лежащей вне окружности, провести к ней две касательные, то
а)длины отрезков от данной точки до точек касания равны;
б)углы между каждой касательной и секущей, проходящей через центр круга, равны.
Рисунок 6 Круг с двумя незначительными дугами, равными по мере. Рисунок 7 Круг с диаметром, перпендикулярным хорде. Учитывая точку вне круга, через эту точку можно провести две линии, которые касаются круга. Касательные отрезки, конечные точки которых являются точками касания и неподвижной точкой вне круга, равны. Другими словами, касательные сегменты, проведенные в один и тот же круг из одной и той же точки, равны.
Рисунок%: Касательные сегменты, которые разделяют конечную точку не по кругу, равны. Аккорды внутри круга могут быть связаны многими способами. Параллельные аккорды в одном круге всегда вырезают конгруэнтные дуги. То есть, дуги, конечные точки которых включают одну конечную точку из каждого аккорда, имеют равные меры.
2. Если из одной точки, лежащей вне окружности, провести к ней касательную и секущую, то квадрат касательной равен произведению секущей на ее внешнюю часть
3. Если две хорды пересекаются в одной точке, то произведение отрезков одной хорды равно произведению отрезков другой.
4. Длина окружности С=2πR;
5. Длина дуги L =πRn/180˚
Когда конгруэнтные аккорды находятся в одном круге, они равноудалены от центра. Рисунок%: Конгруэнтные аккорды в одном круге равноудалены от центра. Последнее слово на аккордах: аккорды одной длины в одном круге обрезают конгруэнтные дуги. То есть, если конечные точки одного аккорда являются конечными точками одной дуги, то две дуги, определенные двумя конгруэнтными аккордами в одном круге, являются конгруэнтными.
Пересечение аккордов, тангенсов и секущих
Ряд интересных теорем возникает из отношений между хордами, секущими сегментами и касательными сегментами, которые пересекаются. Прежде всего, мы должны определить секущий сегмент. Секундный сегмент представляет собой отрезок с одной конечной точкой по кругу, одну конечную точку вне круга и одну точку между этими точками, которые пересекают круг. Существуют три теоремы относительно указанных выше сегментов.
6. Площадь круга S=πR 2
7. Площадь сектора S c =πR 2 n/360

Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Теорема 1. Мера угла между касательной и хордой, имеющими общую точку на окружности, равна половине градусной меры дуги, заключенной между его сторонами
Теорема 2 (о касательной и секущей). Если из точки М к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки М до точки касания равен произведению длин отрезков секущей от точки М до точек её пересечения с окружностью.
Теорема 3 . Если две хорды окружности пересекаются, то произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды, то есть если хорды АВ и СД пересекаются в точке М, то АВ МВ = СМ МД.
Свойства хорд окружности:
Диаметр, перпендикулярный хорде, делит её пополам. Обратно: диаметр, проходящий через середину хорды, перпендикулярен ей.
Равные хорды окружности находятся на равном расстоянии от центра окружности. Обратно: на равного расстоянии от центра окружности находятся равные хорды.
Дуги окружности, заключённые между параллельными хордами равны.
окружности, имеющие общую точку и общую касательную в этой точке, называются)касающимися Если окружности расположены по одну сторону от общей касательной, то они называются касающимися внутренне., а если по разные стороны от касательной, то они называются касающимися внешне.
II . Дополнительные материалы
Свойства некоторых углов.
Теорема.


1) Угол (АВС), вершина которого лежит внутри круга, является полусуммой двух дуг (АС И DE), из которых одна заключена между его сторонами, а другая - между продолжениями сторон.
2) угол (АВС), вершина которого лежит вне круга и стороны пересекаются с окружностью, является полуразностью двух дуг (АС и ED), заключенных между его сторонами
Доказательство.
Проведя хорду АD (на том и на другом чертеже), мы получим ∆АВD,
относительно которого рассматриваемый
угол АВС
служит внешним, когда его
вершина лежит внутри круга, и
внутренним, когда его вершина лежит
вне круга. Поэтому в первом случае:
; во втором случае:
Но углы АDС и DAE, как
вписанные, измеряются половинами
дуг АС и DE; поэтому угол АВС измеряется: в
первом случае суммой: ½ ﬞ AС+1/2 ﬞ
DE, которая равна 1
/
2
(ﮟ
AC+
ﮞ
DE),
а
во втором случае разностью 1 / 2
ﬞ AС- 1 / 2 ﬞ DE,
которая равна 1 / 2 (ﬞ AC-
ﬞ DE). Теорема
. Угол (АCD),
составленный касательной и хордой,
измеряется половиной дуги, заключенной
внутри него. Теперь возьмем общий случай, когда хорда
СD не проходит через центр. Проведя тогда
диаметр СЕ, мы будем иметь: У Пропорциональные
линии в круге
Теорема.
Если через точку (М), взятую внутри круга,
проведена какая-нибудь хорда (АВ) и
диаметр (CD), то произведение
отрезков хорды (АМ МВ) равно произведению
отрезков диаметра (МВ МС). Доказательство. П АМ:
МD=МС: МВ, откуда АМ
МВ=МD МС. Следствие.
Если через точку (М), взятую внутри круга,
проведено сколько угодно хорд (АВ, EF,
KL,...), то произведение
отрезков каждой хорды есть число
постоянное для всех хорд, так как для
каждой корды это произведение равно
произведению отрезков диаметра CD,
проходящего через взятую точку М. Теорема.
Если из точки (М), взятой вне круга,
проведены к нему какая-нибудь секущая
(МА) и касательная (МС), то произведение
секущей на ее внешнюю часть равно
квадрату касательной (предполагается,
что секущая ограничена второй точкой
пересечения, а касательная - точкой
касания). Проведем
вспомогательные хорды АС и ВС; тогда
получим два треугольника МАС и МВС
(покрытые на рисунке штрихами), которые
подобны, потому что у них угол М общий
и углы МСВ и САВ равны, так как каждый
из них измеряется половиной дуги ВС.
Возьмем в ∆МАС стороны МА и МС;
сходственными сторонами в ∆МВС будут
МС и МВ; поэтому МА: МС=МС: МВ, откуда МА
МВ=МС 2 . Следствие.
Если из точки (М), взятой вне круга,
проведено к нему сколько угодно секущих
(МА, MD, МЕ,...), то произведение
каждой секущей на ее внешнюю часть
есть число постоянное для всех секущих,
так как для каждой секущей это
произведение равно квадрату касательной
(МС 2), проведенной из точки М. III
. Вводные задачи.
Задача 1.
В Решение
1) Радиус окружности, описанной около
трапеции, – одно и то же, что и радиус
окружности, описанной около треугольника,
вершинами которого являются любые три
вершины трапеции. Найдем радиус R
окружности, описанной около треугольника
ABD
. 2)
ABCD
– равнобедренная трапеция,
поэтому AK
= MD
, KM
=. В
∆ABK
AK
= AB
cos
A
=
· cos 60° =
.
Значит, BK
= AB
sin
A
=
· = . 3) По теореме
косинусов в
∆ABD
BD
2
= AB
2
+ AD
2
– 2AB
·
AD
cos A
. BD
2
= () 2
+ (3) 2
– 2 ·
· 3
·
= 21 + 9 · 21 – 3 · 21 = 7 · 21; 3) ∆CMN
∾
∆CAB
, значит, ∆CMN
– равносторонний
CM
= CN
= MN
= = 6; P
. А так же
3) BN
= CB
– CN
= 18 – 6 = 12. 4) P (AMNB
)
= AM
+ MN
+ BN
+ AB
= 18 + 6 + 12 + 12 = 48. Около окружности описана равнобокая
трапеция, средняя линия которой равна
5, а синус острого угла при основании
равен 0,8. Найдите площадь трапеции. Решение.
FP
– средняя линия трапеции, значит,
BC
+ AD
= 2FP
. Тогда AB
= CD
= FP
= 5. ∆ABK
– прямоугольный, BK
= AB
sin
A
; BK
= 5 · 0,8
= 4. S (ABCD
)
= FP
· BK
= 5 · 4 = 20. Ответ
:
20. Вписанная
окружность треугольника АВС касается
стороны ВС в точке К, а вневписанная –
в точке L. Докажите, что CK=BL=(a+b+c)/2 Доказательство:
пусть М и N –точки касания вписанной
окружности со сторонами АВ и ВС. Тогда
BK+AN=BM+AM=AB, поэтому СК+CN= a+b-c. Пусть
Р и Q – точки касания вневписанной
окружности с продолжениями сторон АВ
и ВС. Тогда АР=АВ+ВР=АВ+ВL и AQ=AC+CQ=AC+CL.
Поэтому AP+AQ=a+b+c.
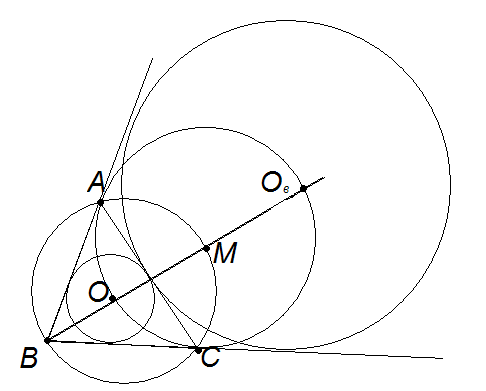
Следовательно, BL=BP=AP-AB=(a+b-c)/2. а)
Продолжение биссектрисы угла В
треугольника АВС пересекает описанную
окружность в точке М. О - центр вписанной
окружности. О В –центр вневписанной
окружности, касающейся стороны АС.
Докажите, что точки А, С, О и O В
лежат на окружности с центром М. Д б) Точка
О, лежащая внутри треугольника АВС,
обладает тем свойством, что прямые АО,
ВО, СО проходят через центры описанных
окружностей треугольников ВСО, АСО,
АВО. Докажите, что О – центр вписанной
окружности треугольника АВС IV
.
Дополнительные задачи
№1.
Окружность, касающаяся гипотенузы
прямоугольного треугольника и продолжений
его катетов, имеет радиус R.
Найдите периметр треугольника Р 1)
∆OAH =∆OAF
по катету и гипотенузе =>HA=FA 2)
∆OCF=∆OCG
=>CF=CG 3)
P ABC =AB+AF+FC+BC=AB+AM+GC+BC+BH+BG=2R №2.
Точки C и D
лежат на окружности с диаметром АВ. АС
∩ BD = Р, а AD
∩ BC = Q.
Докажите, что прямые AB и
PQ перпендикулярны Доказательство:
A №3. В
параллелограмме ABCD диагональ AC больше
диагонали BD; М – точка диагонали AC, BDCM
– вписанный четырехугольник.. Докажите,
что прямая BD является общей касательной
к описанным окружностям треугольников
ABM и ADM П №4. Н Согласно
вводной задаче 4 СМ=(АС+СЕ-АЕ)/2 и
СN=(BC+CE-BE)/2.
Учитывая, что АС=ВС, получаем
МN=|CM-CN|=|AE-BE|/2 №5.
Длины сторон треугольника АВС образуют
арифметическую прогрессию, причем
a Пусть
М середина стороны АС, N- точка касания
вписанной окружности со стороной ВС.
Тогда BN=р–b (вводная задача 4), поэтому
BN=AM, т.к. p=3b/2 по условию. Кроме того,
V
.Задачи
для самостоятельного решения
№1.
Четырехугольник ABCD обладает тем
свойством, что существует окружность,
вписанная в угол BAD и
касающаяся продолжений сторон ВС и CD.
Докажите, что AB+BC=AD+DC. №2.
Общая внутренняя касательная к окружностям
с радиусами R и r пересекает их общие
внешние касательные в точках А и В и
касается одной из окружностей в точке
С. Докажите, что АС∙CB=Rr №3. В
треугольнике АВC угол С
прямой. Докажите, что r =(a+b-c)/2 и r c =(a+b+c)/2 №4. Две
окружности пересекаются в точках А и
В; MN – общая касательная к ним. Докажите,
что прямая АВ делит отрезок MN пополам. №5.
Продолжения биссектрис углов треугольника
АВС пересекают описанную окружность
в точках А 1 , В 1 , С 1 . М –
точка пересечения биссектрис. Докажите,
что: а) MA·MC/MB 1 =2r; b) MA 1 ·MC 1 /MB=R №6.
Угол, составленный двумя касательными,
проведенными из одной точки окружности,
равен 23 о 15`. Вычислить дуги,
заключенные между точками касания №7.
Вычислить угол, составленный касательной
и хордой, если хорда делит окружность
на две части, относящиеся как 3:7. VI. Контрольные
задачи.
Вариант
1. Точка М находится вне круга с центром
О. Из точки М проведены три секущие:
первая пересекает окружность в точках
В и А (М-В-А), вторая – в точках D и C
(М-D-C), а третья пересекает окружность в
точках F и E (M-F-E)
и проходит через центр окружности, АВ
= 4, ВМ =5, FM = 3. Докажите,
что если АВ = СD, то углы АМЕ и СМЕ равны. Найдите
радиус окружности. Найдите
длину касательной, проведенной из
точки М к окружности. Найдите
угол АЕВ. Вариант
2. АВ – диаметр окружности с центром О.
Хорда ЕF пересекает диаметр в точке К
(А-К-О), ЕК =4, КF = 6, ОК = 5. Найдите
радиус окружности. Найдите
расстояние от центра окружности до
хорды ВF. Найдите
острый угол между диаметром АВ и хордой
EF. Чему
равна хорда FМ, если ЕМ –
параллельная АВ. Вариант
3.
В
прямоугольный треугольник АВС ( Вариант
4. АВ – диаметр окружности с центром О.
Радиус этой окружности равен 4, О 1 –
середина ОА. С центром в точке О 1
проведена окружность, касающаяся большей
окружности в точке А. Хорда
СD большей окружности
перпендикулярна к АВ и пересекает АВ в
точке К. Е и F –точки пересечения СD с
меньшей окружностью (С-Е-К-F-D), АК=3. Найдите
хорды АЕ и АС. Найдите
градусную меру дуги АF и её длину. Найдите
площадь части меньшего круга, отсеченной
хордой ЕF. Найдите
радиус окружности, описанной около
треугольника АСЕ.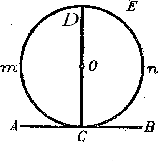 Предположим
сначала, что хорда СD
проходит через центр О, Т.е. что хорда
есть диаметр. Тогда угол АС
D
-
прямой и, следовательно, равен 90°. Но
и половина дуги СmD также равна 90°, так
как целая дуга СmD, составляя полуокружность,
содержит 180°. Значит теорема оправдывается
в этом частном случае..
Предположим
сначала, что хорда СD
проходит через центр О, Т.е. что хорда
есть диаметр. Тогда угол АС
D
-
прямой и, следовательно, равен 90°. Но
и половина дуги СmD также равна 90°, так
как целая дуга СmD, составляя полуокружность,
содержит 180°. Значит теорема оправдывается
в этом частном случае.. гол
ACE, как составленный касательной и
диаметром, измеряется, по доказанному,
половиной дуги CDE; Угол DCE, как вписанный,
измеряется половиной дуги CnED: разница
в доказательстве только та, что этот
угол надо рассматривать не как разность,
а как сумму прямого угла ВСЕ и острого
угла ECD.
гол
ACE, как составленный касательной и
диаметром, измеряется, по доказанному,
половиной дуги CDE; Угол DCE, как вписанный,
измеряется половиной дуги CnED: разница
в доказательстве только та, что этот
угол надо рассматривать не как разность,
а как сумму прямого угла ВСЕ и острого
угла ECD. роведя
две вспомогательные хорды АС и ВD,
мы получим два треугольника АМС и MBD
(покрытые на рисунке штрихами), которые
подобны, так как у них углы А и D
равны, как вписанные, опирающиеся на
одну и ту же дугу ВС, углы С и В равны,
как вписанные, опирающиеся на одну и ту
же дугу AD. Из подобия
треугольников выводим:
роведя
две вспомогательные хорды АС и ВD,
мы получим два треугольника АМС и MBD
(покрытые на рисунке штрихами), которые
подобны, так как у них углы А и D
равны, как вписанные, опирающиеся на
одну и ту же дугу ВС, углы С и В равны,
как вписанные, опирающиеся на одну и ту
же дугу AD. Из подобия
треугольников выводим: Доказательство.
Доказательство. равнобедренной трапеции с острым углом
в 60° боковая сторона равна
,
а меньшее основание
- . Найдите радиус
окружности, описанной около этой
трапеции.
равнобедренной трапеции с острым углом
в 60° боковая сторона равна
,
а меньшее основание
- . Найдите радиус
окружности, описанной около этой
трапеции.
AD
=
.
BD
=
.CD
= 3 · CP
.![]()
 Так как окружность вписана в четырехугольник,
то BC
+ AD
= AB
+ CD
. Этот
четырехугольник – равнобокая трапеция,
значит BC
+ AD
= 2AB
.
Так как окружность вписана в четырехугольник,
то BC
+ AD
= AB
+ CD
. Этот
четырехугольник – равнобокая трапеция,
значит BC
+ AD
= 2AB
.
 оказательство:
Так как
оказательство:
Так как![]() Доказательство:
Пусть Р- центр описанной окружности
треугольника АСО. Тогда
Доказательство:
Пусть Р- центр описанной окружности
треугольника АСО. Тогда ешение:
HOGB- квадрат со стороной
R
ешение:
HOGB- квадрат со стороной
R D
– диаметр => вписанный угол ADB=90
o (как опирающийся
на диаметр)=> QD/QP=QN/QA;
∆QDP
подобен ∆QNA
по 2м сторонам и углу между ними=>
QN
перпендикулярна AB .
D
– диаметр => вписанный угол ADB=90
o (как опирающийся
на диаметр)=> QD/QP=QN/QA;
∆QDP
подобен ∆QNA
по 2м сторонам и углу между ними=>
QN
перпендикулярна AB . усть
О – точка пересечения диагоналей АС и
ВD. Тогда MO·
OC=BO·
ОD.
Тогда как ОС=ОА и ВО=ВD, то МО·
ОА=ВО 2
и МО·
ОА=DO 2 .
Эти равенства означают, что ОВ касается
описанной окружности треугольника ADM
усть
О – точка пересечения диагоналей АС и
ВD. Тогда MO·
OC=BO·
ОD.
Тогда как ОС=ОА и ВО=ВD, то МО·
ОА=ВО 2
и МО·
ОА=DO 2 .
Эти равенства означают, что ОВ касается
описанной окружности треугольника ADM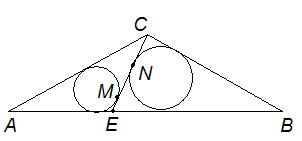 а
основании АВ равнобедренного треугольника
АВС взята точка Е, и в треугольники АСЕ
и АВЕ вписаны окружности, касающиеся
отрезка СЕ в точках М и N . Найдите длину
отрезка MN, если известны длины АЕ и ВЕ.
а
основании АВ равнобедренного треугольника
АВС взята точка Е, и в треугольники АСЕ
и АВЕ вписаны окружности, касающиеся
отрезка СЕ в точках М и N . Найдите длину
отрезка MN, если известны длины АЕ и ВЕ.



















