Trijstūra ierobežotā apļa diametrs. Nodarbības kopsavilkums "ierobežots aplis". Kā atrast ap trijstūri norobežota apļa rādiusu - vispārīgā formula
Šajā daļā mēs apspriedīsim ierobežoto apli ap trīsstūri (bieži teikts "tuvumā"). Vispirms sniegsim definīciju.
1. Noteiktā apļa esamība un centrs
Šeit rodas jautājums: vai šāds aplis pastāv jebkuram trīsstūrim? Izrādās, ka jā, visiem. Un turklāt tagad mēs formulēsim teorēmu, kas arī atbild uz jautājumu, kur ir ierobežotā apļa centrs.
Formulas taisnstūra diagonāles garuma atrašanai
Formula taisnstūra malā ar diametru un leņķi β. To sauc par taisnstūra diagonāli jebkuram segmentam, kas savieno divas taisnstūra pretējo stūru virsotnes. Taisnstūra diagonāles formula taisnstūra divu malu izteiksmē.
Formula taisnstūra diagonālei laukumā un abās pusēs. Formula taisnstūra diagonālei pa perimetru un abās pusēs. Taisnstūra diagonāles formula ierobežotā apļa rādiusa izteiksmē. Formula taisnstūra diagonālei gar apļa apkārtmēru.
Skaties šādi:
Apkoposim drosmi un pierādīsim šo teorēmu. Ja jau esat izlasījis tēmu “”, izdomājis, kāpēc trīs bisektrise krustojas vienā punktā, tad tev būs vieglāk, bet, ja neesi izlasījis, neuztraucies: tagad mēs visu izdomāsim ārā.
Mēs veiksim pierādīšanu, izmantojot punktu lokusa (LPT) jēdzienu.
Taisnstūra diagonāles formula, kas izteikta diagonālei blakus esošā leņķa sinusa izteiksmē un šim leņķim pretējās malas garumā. Taisnstūra diagonāles formula, kas izteikta diagonālei piegulošā leņķa kosinusa izteiksmē un šim leņķim blakus esošās malas garumam. Taisnstūra diagonāles formula akūtā leņķa sinusa izteiksmē starp diagonālēm un taisnstūra laukumu.
Formulas taisnstūra perimetra garuma noteikšanai
Taisnstūra perimetru sauc par taisnstūra visu malu garumu summu. Taisnstūra perimetra formula taisnstūra divu malu izteiksmē. Taisnstūra perimetra formula, ņemot vērā laukumu un abas malas. Formula taisnstūra perimetram pa diagonāli un abās pusēs.
Nu, piemēram, vai bumbiņu komplekts ir apaļu priekšmetu "ģeometriskā vieta"? Nē, protams, jo ir apaļi... arbūzi. Bet vai cilvēku kopums, “ģeometriskā vieta”, spēj runāt? Ne, jo ir mazuļi, kuri neprot runāt. Dzīvē parasti ir grūti atrast reālas “punktu ģeometriskās vietas” piemēru. Ģeometrija ir vienkāršāka. Šeit, piemēram, ir tikai tas, kas mums nepieciešams:
Taisnstūra perimetra formula ierobežotā apļa rādiusa izteiksmē un abās pusēs. Taisnstūra perimetra formula, ņemot vērā ierobežotā apļa diametru un abas malas. To sauc par taisnstūra laukumu telpā, ko ierobežo taisnstūra malas, tas ir, taisnstūra perimetra zonā.
Formulas taisnstūra laukuma noteikšanai
Formula taisnstūra laukumam ar divām malām. Formula taisnstūra laukumam pa perimetru un abās pusēs. Formula taisnstūra laukumam pa diagonāli un abās pusēs. Formula taisnstūra laukumam gar diagonāli un akūtā leņķa sinusa starp diagonālēm.
Šeit kopa ir vidējais perpendikuls, un īpašība "" ir "būt vienādā attālumā (punktam) no segmenta galiem."
Pārbaudīsim? Tātad, jums ir jāpārliecinās par divām lietām:
Savienojiet ar un ar. Tad līnija ir mediāna un augstums collas. Tātad, - vienādsānu, - mēs pārliecinājāmies, ka jebkurš punkts, kas atrodas uz perpendikulāras bisektriseles, ir vienlīdz tālu no punktiem un.
Aplis, kas norobežots ap taisnstūri
Taisnstūra laukuma formula, ņemot vērā ierobežotā apļa rādiusu un jebkuru malu. Taisnstūra laukuma formula aplī ir apļa aplis un abās pusēs. To sauc par apli, kas robežojas ap taisnstūri, līdz aplim, kas iet caur četrām taisnstūra virsotnēm, kura centrs ir taisnstūra diagonāļu krustpunkts.
Formulas ap taisnstūri norobežota riņķa rādiusa atrašanai
Formula apļa rādiusam, ko ierobežo taisnstūris caur divām malām. Formula apļa rādiusam, kas apvilkts ap taisnstūri pa kvadrāta perimetru un abām pusēm. Apļa rādiusa formula ap taisnstūri ir aprakstīta taisnstūra laukuma un tā vienas malas garuma izteiksmē.
Paņem - vidu un savieno un. Ieguva vidējo. Bet - vienādsānu pēc nosacījuma, ne tikai mediāna, bet arī augstums, tas ir, mediāna perpendikulāra. Tas nozīmē, ka punkts atrodas tieši uz perpendikulārās bisektrise.
Visi! Mēs esam pilnībā pārbaudījuši faktu, ka segmenta perpendikulārā bisektrise ir punktu atrašanās vieta, kas atrodas vienādā attālumā no segmenta galiem.
Formula apļa rādiusam, kas apvilkts ap taisnstūri gar taisnstūra diagonāli. Formula apļa rādiusam, kas aprakstīts ap taisnstūri ar apļa apkārtmēra diametru. Formula apļa rādiusam, kas aprakstīts ap taisnstūri, ņemot vērā diagonālei blakus esošā leņķa sinusu un šim leņķim pretējās malas garumu.
Aplis, kas ieskauj doto daudzstūri, ir ierobežots aplis. Lielākā daļa cilvēku ir dzirdējuši terminus apkārtmērs un rādiuss, taču ierobežots aplis ir mazāk pazīstams termins. Iedomājieties 2D daudzstūri ar taisnām malām, piemēram, trīsstūri. Iedomājieties apli ap trijstūri tā, lai tas skar visas trīs tā virsotnes; tas ir ierobežots loks. Lai aprēķinātu rādiusu, izmantojiet vienkāršu algebru un kalkulatoru.
Tas viss ir labi, bet vai mēs esam aizmirsuši par ierobežoto loku? Nebūt ne, mēs vienkārši sagatavojām sev "tilta galviņu uzbrukumam".
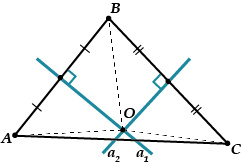
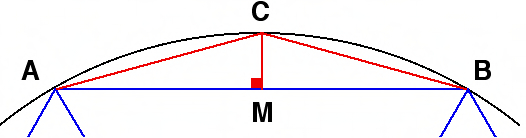
Apsveriet trīsstūri. Uzzīmēsim divus vidējos perpendikulus un, teiksim, uz nogriežņiem un. Tie kādā brīdī krustosies, ko mēs nosauksim.
Pārbaudiet visus savus mērījumus un pārliecinieties, vai kompass norāda, ka tas nemainās, kamēr riņķojat.
- Ir ārkārtīgi svarīgi precīzi un precīzi izmērīt.
- Ne visiem daudzstūriem var būt ierobežots aplis.
Tādējādi sešstūrī ierakstītā apļa laukums ir vienāds ar. Tagad mēs vēršamies pie ierakstītā kvadrāta. Tā kā kvadrāta diagonāle ir vienāda ar saknes laiku malu, mums ir. Tad kvadrātā ierakstītā apļa rādiusam būs puse no malas izmēra. Tādējādi jūs redzēsit, ka trijstūrī ierakstīta riņķa rādiuss ir puse no trijstūrī norobežotā riņķa rādiusa, jo riņķa apkārtmēru apraksta ar sadalītu vidi divās daļās, kas ir proporcionālas 1, un tad rādiuss. no ierakstītā apļa būs.
Un tagad, uzmanību!
Punkts atrodas uz perpendikulāras bisektrise;
punkts atrodas uz perpendikulāras bisektrise.
Un tas nozīmē un.
No tā izriet vairākas lietas:
Pirmkārt, punktam jāatrodas uz segmenta trešās perpendikulāras bisektrise.
Apļa mērīšana un tuvināšana
Tādējādi ierakstītā apļa laukums būs. Un problēma ir pierādīt, ka šo laukumu summa ir vienāda ar iekšējā apļa laukumu. Tātad, veiksim vainagu laukumu summu. Šī ir vainagu laukumu summa. Var redzēt, ka mums ir 3 staru apļi. Šis raksts piedāvā hipotēzi, ieganstu, lai apsvērtu dažus šī perioda matemātikas punktus Mezopotāmijā.
Veidojot apli starp diviem sešstūriem, kuru perimetru var viegli aprēķināt, pēc tam secīgi dubultojot malu skaitu, viņš iegūst rāmi ar daudzstūriem ar 96 malām. Iespējams, ir vieglāk novērtēt veiktspēju, norādot skaitliskas vērtības.
Tas nozīmē, ka perpendikulārajai bisektrisei arī jāiet cauri punktam, un visas trīs perpendikulārās bisektrise krustojas vienā punktā.
Otrkārt: ja mēs uzzīmēsim apli ar centru ar punktu un rādiusu, tad arī šis aplis ies caur punktu un caur punktu, tas ir, tas būs ierobežotais aplis. Tas nozīmē, ka jau pastāv, ka trīs perpendikulāro bisektriņu krustpunkts ir jebkura trijstūra ierobežotā apļa centrs.
Šeit mēs redzam novērošanas metožu interesi un efektivitāti: no vienas puses, tās sniedz tuvinājumu, un, no otras puses, ļauj kontrolēt perfektu kļūdu. Cik man zināms, Arhimēds ir pirmais, kas skaidri pamato savus rezultātus attiecībā uz apli, un soli pa solim sniedz virkni argumentu, kas izskaidro, kāpēc viņa apgalvojumi ir patiesi. Taču viņš nav pirmais, kurš interesējas par apli un tā mēru. Mums ir ļoti seni pierādījumi, viens Ēģiptē un daži citi Mezopotāmijā, kas dodas šajā virzienā.
Un ir dažas "babiloniešu" māla tabletes, kas datētas ar to pašu periodu un gar diska perimetru vai laukumu. Šī ir šī raksta tēma. Pastaiga var sākties, bet pirms došanās uz Babilonu 17. vai 18. gadsimtā pirms mūsu ēras. Ir atrasta Babilonijas māla plāksne, kas parāda sešstūra perimetra attiecību pret tā ierobežotā apļa perimetru.
Un pēdējā lieta: par unikalitāti. Ir skaidrs (gandrīz), ka punktu var iegūt unikālā veidā, un tāpēc arī aplis ir unikāls. Nu, "gandrīz" - mēs to atstāsim jūsu ziņā. Šeit mēs esam pierādījuši teorēmu. Var kliegt "Urā!".
Un, ja problēma ir jautājumā "atrast ierobežotā apļa rādiusu"? Vai otrādi, rādiuss ir dots, bet jāatrod kaut kas cits? Vai ir kāda formula, kas attiecas uz ierobežotā apļa rādiusu ar citiem trijstūra elementiem?
Un tie bieži tiek pievienoti vienā vai otrā veidā. Šī bija otrā problēma, kas man radīja problēmu: vai babilonieši patiešām varēja eksperimentāli atrast šo vērtību? Šobrīd pieredze ir ērti lietojama, ar šuvēju skaitītāju un dažāda diametra ikdienas priekšmetiem: pannu, katliņu, skārda kārbām. Tiek izmērīts perimetrs un diametrs, un tiek veikts dalījums. Atšķirības bija trešajā zīmē aiz komata. Protams, nav ne tik precīzu rūpniecisku priekšmetu, ne šuvēju milimetros graduētu skaitītāju.
Mērīšanai tas ir plānāks: virve, ādas siksna, var izstiepties zem sasprindzinājuma un viegli sarauties. Savukārt kaltēta papirusa miza nepagarinās. Diemžēl man tā nebija. Acīmredzot tie nav graduēti, bet tas nav nopietni: mūs interesē divu garumu attiecība: no perimetra un diametra, nevis no pašiem garumiem. Ar rotangpalmu ir viegli apbraukt priekšmetu un to sagriezt. Interesanti, ka ir mazāk viegli precīzi nogriezt rotangpalmas diegu, lai tas atbilstu diametram. Patiešām, keramikas augšējā mala bieži ir noapaļota.
Ļoti bieži, risinot ģeometriskos uzdevumus, ir jāveic darbības ar palīgfigūrām. Piemēram, atrodiet ierakstīta vai ierobežota apļa rādiusu utt. Šis raksts parādīs, kā atrast trijstūri apņemoša apļa rādiusu. Vai, citiem vārdiem sakot, apļa rādiuss, kurā trīsstūris ir ierakstīts.
Tāpēc ir jānostiprina rotangpalma pa perimetru un pēc tam jānogriež otrais rotangpalmas nazis, kas atbilst pirmā iekšējam diametram. Atliek aprēķināt divu garumu attiecību, tos nezinot precīzas vērtības, ko var izdarīt, atgriežoties pie pašas dalīšanas sākuma. 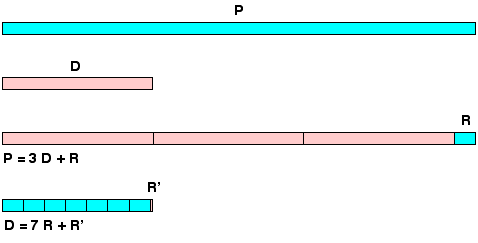
Mans labākais sniegums bija 6, 8 reizes, tas ir 6 reizes, ar brīnišķīgu atpūtu. Tomēr šie eksperimenti mani pārliecināja, ka babilonieši nesaņēma eksperimentālu vērtību, vismaz ne no šī maršruta. Bet šajā gadījumā rodas divi jautājumi.
Kā atrast ap trijstūri norobežota apļa rādiusu - vispārīgā formula
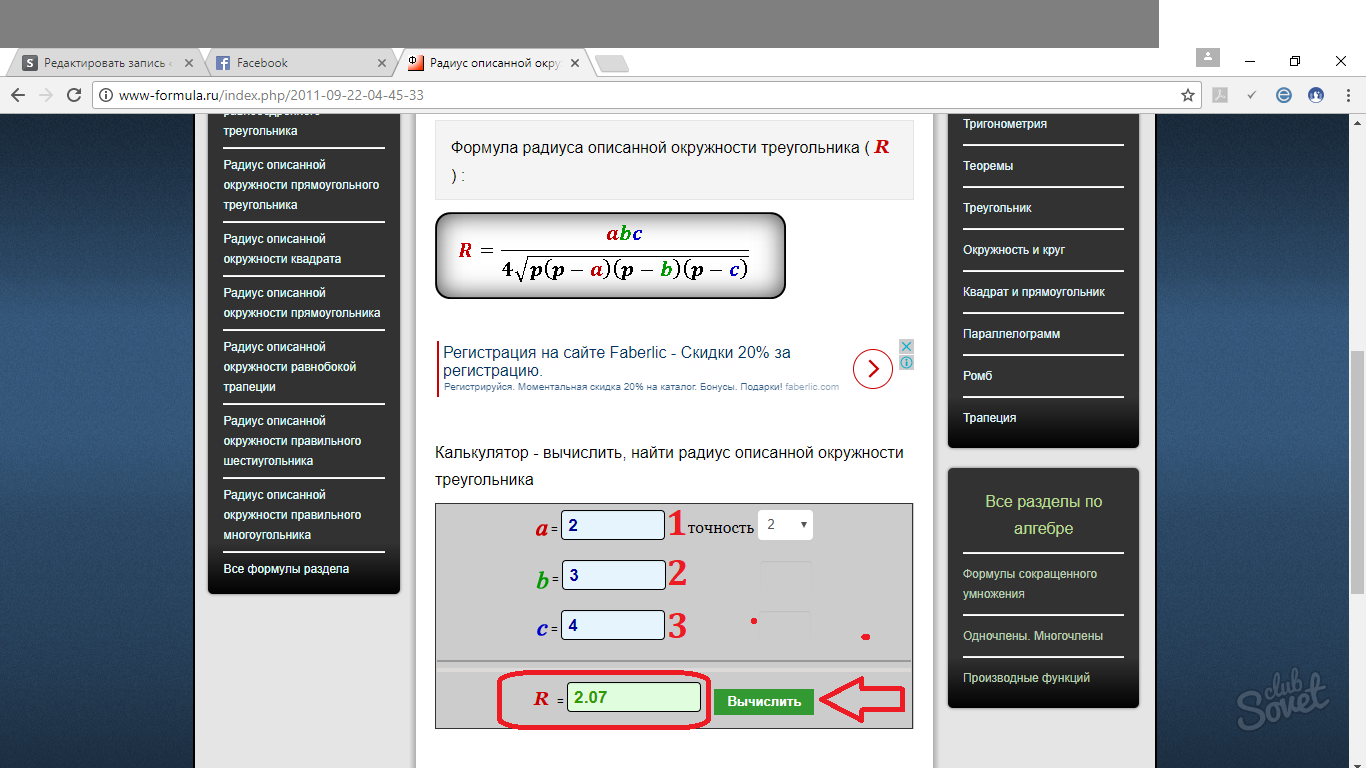
Vispārīgā formula ir šāda: R = abc/4√p(p - a)(p - b)(p - c), kur R ir ierobežotā apļa rādiuss, p ir trīsstūra perimetrs, dalīts ar 2 (pusperimetrs). a, b, c ir trijstūra malas.
Atrodiet trīsstūra apļa rādiusu, ja a = 3, b = 6, c = 7.
1. jautājums: ja tas nav eksperimentāls, tas ir teorētisks, ģeometrisks. 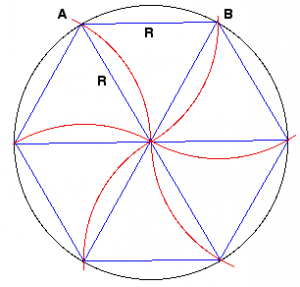
Tādējādi apļa perimetrs P ir lielāks par sešstūra perimetru, un attiecība starp tiem ir vienāda. Mums ir diezgan dabiski novērtēt apļa perimetru, kas nav zināms attiecībā pret to, kas ir zināms pašam sešstūrim.
Vēlāk redzēsim, ko par to domāt. 1. hipotēze: Babilonieši zināja Pitagora teorēmu tūkstoš gadus iepriekš. 2. hipotēze: viņi zināja, ka ir atraduši veselu skaitļu malu taisnstūrus. Varbūt ne visi, bet vismaz tie, kuru hipotenūza un viena no malām ir veseli veseli skaitļi.
Tādējādi, pamatojoties uz iepriekš minēto formulu, mēs aprēķinām pusperimetru:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Aizstājiet vērtības formulā un iegūstiet:
R = 3 x 6 x 7/4√8 (8 - 3) (8 - 6) (8 - 7) = 126/4√ (8 x 5 x 2 x 1) = 126/4√80 = 126/16 √5.
Atbilde: R = 126/16√5
Kā atrast ap vienādmalu trīsstūri apvilkta riņķa rādiusu
Lai atrastu ap vienādmalu trīsstūri norobežota riņķa rādiusu, ir diezgan vienkārša formula: R = a/√3, kur a ir tā malas izmērs.
Protams, nekas neliecina, ka babilonieši to būtu izdarījuši. To var paveikt tikai jaunas māla tabletes atklāšana. Turklāt šī ideja ir balstīta uz hipotēzi 1, un vai babilonieši tiešām prata atrast šādus trīsstūrus? 
Pēdējās 15 rindas ir sadalītas 4 kolonnās, no kurām pirmās divas rindiņas nosaka saturu. 4. ailē ir zīme, kam seko skaitļi no 1 līdz.
Piemērs: Vienādmalu trijstūra mala ir 5. Atrodiet ierobežotā apļa rādiusu.
Tā kā visas vienādmalu trīsstūra malas ir vienādas, lai atrisinātu problēmu, jums vienkārši jāievada tā vērtība formulā. Mēs iegūstam: R = 5/√3.
Atbilde: R = 5/√3.
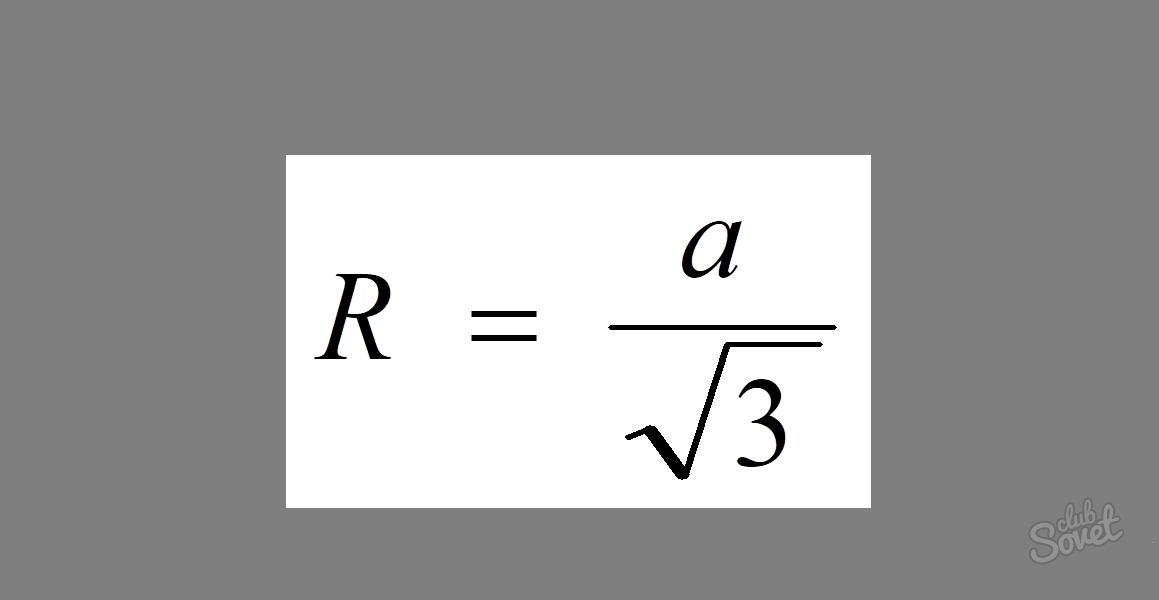
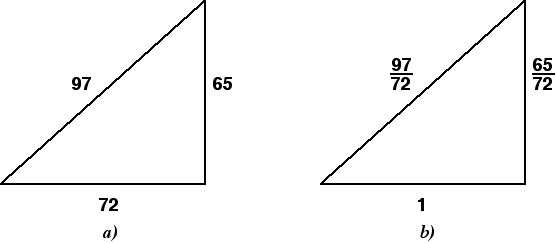
Kā atrast apļa rādiusu, kas ir ierobežots ap taisnleņķa trīsstūri
Formula izskatās šādi: R = 1/2 × √(a² + b²) = c/2, kur a un b ir kājas un c ir hipotenūza. Ja saskaitām taisnleņķa trīsstūrī esošo kāju kvadrātus, iegūstam hipotenūzas kvadrātu. Kā redzams no formulas, šī izteiksme atrodas zem saknes. Aprēķinot hipotenūzas kvadrāta sakni, mēs iegūstam pašu garumu. Reizinot iegūto izteiksmi ar 1/2, galu galā tiek iegūta izteiksme 1/2 × c = c/2.
1., 2. un 3. kolonna attiecas uz taisnleņķa trijstūriem. 2. un 3. kolonna attiecīgi norāda katra trīsstūra mazāko malu un hipotenūzu. 1. ailē ir norādīts koeficienta kvadrāts abās labā stūra pusēs. Piemēram, 5. rinda sākas seksuālajā sistēmā.
Tas ir pārāk precīzs, lai būtu patiesība, taču varat pārbaudīt, vai tas attiecas uz citām virknēm. Pastāv strīdi par metodēm, kuras babilonieši varētu būt izmantojuši šīs tabulas sastādīšanai. Ir arī kļūdas rakstnieka eksemplārā un mazi noslēpumi, piemēram, 11. rindiņa, kurā kā malas ir norādīti 45 un 1 15, tas ir, decimālskaitlī: 45, un abi ir 15 reizinātāji, un šis trīsstūris nav nekas cits kā trīsstūris. no sāniem. Kāpēc tas nav dots šādā formā, daudz vienkāršāk? Un kāda varētu būt priekšrocība, piešķirot slīpuma kvadrātu, nevis pašu slīpumu?
Piemērs: Aprēķiniet ierobežotā apļa rādiusu, ja trijstūra kājas ir 3 un 4. Ievietojiet vērtības formulā. Mēs iegūstam: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2,5.
Šajā izteiksmē 5 ir hipotenūzas garums.
Atbilde: R = 2,5.
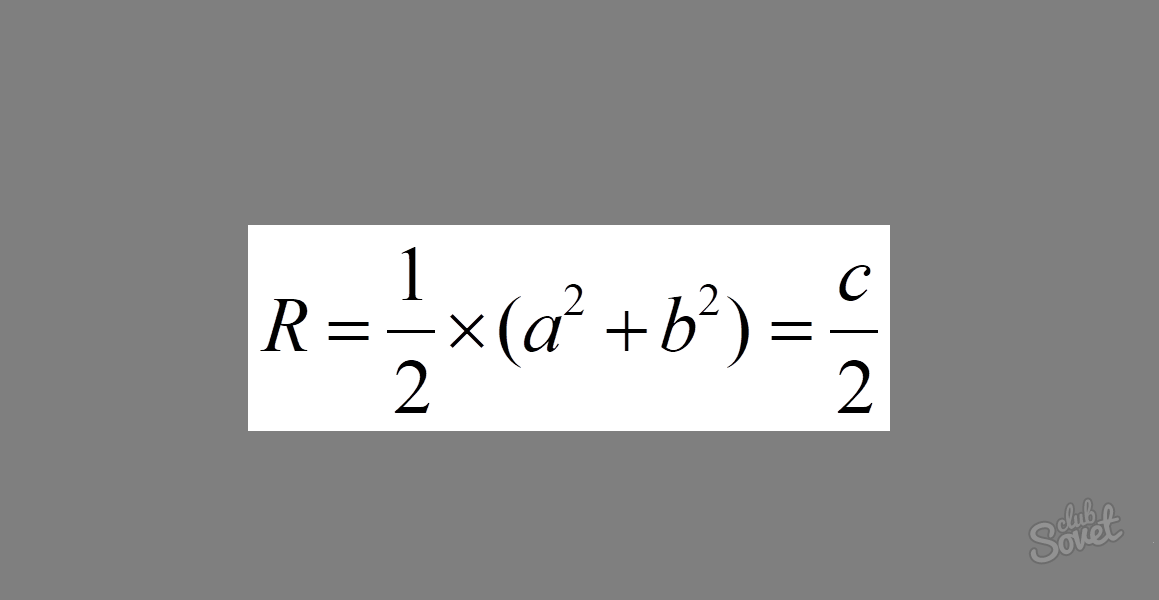
Kā atrast ap vienādsānu trīsstūri apzīmēta riņķa rādiusu
Formula izskatās šādi: R = a² / √ (4a² - b²), kur a ir trijstūra augšstilba garums un b ir pamatnes garums.
Piemērs: Aprēķiniet apļa rādiusu, ja tā gurns = 7 un tā pamatne = 8.
Risinājums: šīs vērtības aizstājam ar formulu un iegūstam: R \u003d 7² / √ (4 × 7² - 8²).
R = 49/√(196–64) = 49/√132. Atbildi var uzrakstīt tieši šādi.
Atbilde: R = 49/√132
Tiešsaistes resursi apļa rādiusa aprēķināšanai
Visās šajās formulās ir ļoti viegli apjukt. Tāpēc, ja nepieciešams, varat izmantot tiešsaistes kalkulatori, kas palīdzēs atrisināt problēmas ar rādiusa atrašanu. Šādu mini programmu darbības princips ir ļoti vienkāršs. Attiecīgajā laukā aizstājiet malas vērtību un saņemiet gatavu atbildi. Varat izvēlēties vairākas atbildes noapaļošanas iespējas: līdz decimāldaļām, simtdaļām, tūkstošdaļām utt.