У цій частині ми обговоримо коло, описане навколо (часто кажуть «біля») трикутника. Насамперед дамо визначення.

1. Існування та центр описаного кола

Тут виникає запитання: а чи для будь-якого трикутника існує таке коло? Ось виявляється, що так, для кожного. Більше того, ми зараз сформулюємо теорему, яка ще й відповідає на питання, де ж знаходиться центр описаного кола.

Дивись, ось так:

Давай наберемося мужності та доведемо цю теорему. Якщо ти вже читав тему « » розбирався в тому, чому ж три бісектриси перетинаються в одній точці, то тобі буде легше, але і якщо не читав - не переживай: зараз у всьому розберемося.

Доказ проводитимемо, використовуючи поняття геометричного місця точок (ГМТ).

Ну от, наприклад, чи є безліч м'ячів – геометричним місцем круглих предметів? Ні, звичайно, тому що бувають круглі кавуни. А чи є безліч людей, «геометричним місцем», які вміють говорити? Теж ні, бо є немовлята, які не вміють говорити. У житті взагалі складно знайти приклад справжнього геометричного місця точок. У геометрії простіше. Ось, наприклад, саме те, що нам потрібно:

Тут безліч - це серединний перпендикуляр, а властивість "" - це "бути рівновіддаленою (точкою) від кінців відрізка".

Перевіримо? Отже, потрібно впевнитись у двох речах:

З'єднаємо з і с. Тоді лінія є медіаною та висотою ст. Значить, рівнобедрений, переконалися, що будь-яка точка, що лежить на серединному перпендикулярі, однаково віддалена від точок і.

Візьмемо – середину і з'єднаємо в. Вийшла медіана. Але – рівнобедрений за умовою не лише медіана, а й висота, тобто – серединний перпендикуляр. Значить, точка – точно лежить на серединному перпендикулярі.

Всі! Повністю перевірили те що, що серединний перпендикуляр до відрізка є геометричним місцем точок, рівновіддалених від кінців відрізка.

Це все добре, але чи не забули ми про описане коло? Зовсім ні, ми якраз підготували собі «плацдарм для нападу».

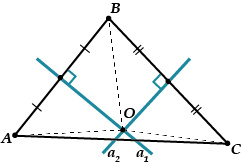
Розглянемо трикутник. Проведемо два серединні перпендикуляри і, скажімо, до відрізків і. Вони перетнуться в якійсь точці, яку ми назвемо.

А тепер, увага!

Крапка лежить на серединному перпендикулярі;
точка лежить на серединному перпендикулярі.
Отже, в.

Звідси випливає відразу кілька речей:

По перше, точка повинна лежати третьому серединному перпендикулярі, до відрізку.

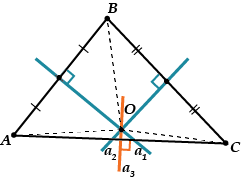
Тобто серединний перпендикуляр теж повинен пройти через точку, і всі три серединні перпендикуляри перетнулися в одній точці.

По-друге: якщо ми проведемо коло з центром у точці і радіусом, то це коло також пройде і через точку, і через точку, тобто буде описаним колом. Отже, вже є, що перетин трьох перпендикулярів – центр описаного кола для будь-якого трикутника.

І останнє: про єдиність. Ясно (майже), що точку можна отримати єдиним чином, тому й коло – єдине. Ну, а "майже" - залишимо на твоє роздуми. Ось і довели теорему. Можна кричати "Ура!".

А якщо в задачі стоїть питання «знайдіть радіус описаного кола»? Або навпаки, радіус дано, а потрібно знайти щось інше? Чи є формула, що зв'язує радіус описаного кола з іншими елементами трикутника?

Визначення

Окружність \(S\) описана біля багатокутника \(P\), якщо всі вершини багатокутника \(P\) лежать на колі \(S\).

У цьому випадку багатокутник (P) називається вписаним в коло.

Визначення

Серединний перпендикуляр до відрізка - це пряма, що проходить через середину даного відрізка перпендикулярно до нього.

Теорема

Кожна точка серединного перпендикуляра до відрізка рівновіддалена від кінців цього відрізка.

Доведення

Розглянемо відрізок (AB) і серединний перпендикуляр (a) до нього. Доведемо, що з будь-якої точки \(X\in a\) виконано: \(AX=BX\) .

Розглянемо \(\triangle AXB\) : відрізок \(XO\) є медіаною і висотою, отже, \(\triangle AXB\) - рівнобедрений, отже, \(AX=BX\) .

Теорема

Серединні перпендикуляри до сторін трикутника перетинаються лише у точці.

Доведення

Розглянемо \(\triangle ABC\). Проведемо серединні перпендикуляри до сторін (AB) і (AC). Вони перетнуться в точці \(O\) .

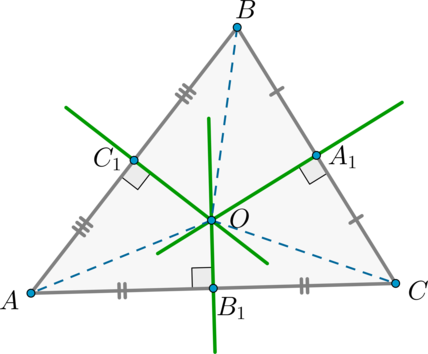
По попередній теоремі для серединного перпендикуляра \(C_1O\) виконано: \(AO=BO\) , а для (B_1O\) - \(AO=CO\) . Отже, (BO = CO) . Значить, \(\triangle BOC\) - рівнобедрений, отже, висота \(OA_1\), проведена до основи \(BC\), буде також і медіаною. Значить, \(OA_1\) - серединний перпендикуляр до відрізка \(BC\).

Таким чином, всі три серединні перпендикуляри перетнулися в одній точці (O).

Слідство

Якщо точка рівновіддалена від кінців відрізка, вона лежить на його серединному перпендикулярі.

Теорема

Біля будь-якого трикутника можна описати єдине коло, причому центр описаного кола є точка перетину серединних перпендикулярів до сторін трикутника.

Доведення

З доведеної вище теореми випливає, що (AO = BO = CO) . Отже, всі вершини трикутника рівновіддалені від точки (O), отже, вони лежать на одному колі.

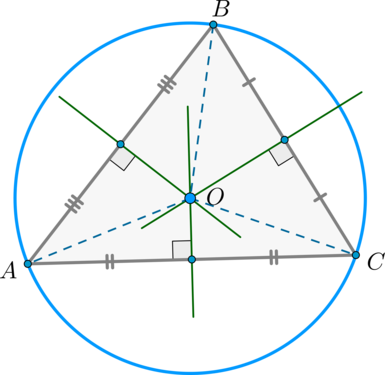
Таке коло єдине. Припустимо, що близько \(\triangle ABC\) можна описати ще одне коло. Тоді її центр повинен збігтися з точкою \(O\) (т.к. це єдина точка, рівновіддалена від вершин трикутника), а радіус повинен дорівнювати відстані від центру до якоїсь з вершин, тобто. \ (OA \). Т.к. у цих кіл збігаються і центр, і радіус, то й ці кола збігаються.

Теорема про площу вписаного трикутника

Якщо \(a, b, c\) - сторони трикутника, а \(R\) – радіус описаного біля нього кола, то площа трикутника \

Доведення*
З доказом цієї теореми рекомендується ознайомитись після вивчення теми “Теорема синусів”.

Позначимо кут між сторонами (a) і (c) за (alfa). Тоді \(S_(\triangle)=\frac12 ac\cdot \sin \alpha\).

По теоремі синусів \(\dfrac b(\sin\alpha) = 2R\), звідки \(\sin \alpha=\dfrac b(2R)\). Отже, \(S_(\triangle)=\dfrac(abc)(4R)\).

Теорема

Біля чотирикутника можна описати коло тоді й тільки тоді, коли суми його протилежних кутів дорівнюють \(180^\circ\) .

Доведення

Необхідність.

Якщо близько чотирикутника \(ABCD\) можна описати коло, то \(\buildrel\smile\over(ABC) + \buildrel\smile\over(ADC) = 360^\circ\), звідки \(\angle ABC + \angle ADC = \frac(1)(2)\buildrel\smile\over(ABC) + \frac(1)(2)\buildrel\smile\over(ADC) = \frac(1 )(2)(\buildrel\smile\over(ABC) + \buildrel\smile\over(ADC)) = 180^\circ\). Для кутів (BCD) і (BAD) аналогічно.

Достатність.

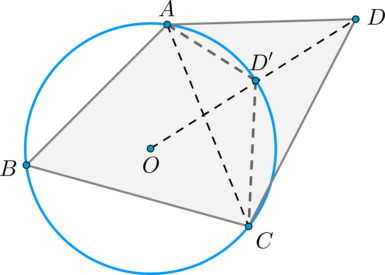
Опишемо коло біля трикутника (ABC). Нехай центр цього кола - точка \ (O \). На прямій, що проходить через точки \(O\) і \(D\) відзначимо точку \(D"\) перетину цього прямого і кола. Припустимо, що точки \(D\) і \(D"\) не збіглися, тоді розглянемо чотирикутник \(CD"AD\).

Кути \(CD"A\) і \(CDA\) доповнюють кут \(ABC\) до \(180^\circ\) (\(\angle CDA\) доповнює за умовою, а \(\angle CD"A \) за доведеним вище), отже, вони рівні, але тоді сума кутів чотирикутника \(AD"CD\) більше \(360^\circ\) , чого бути не може (сума кутів це чотирикутника є сума кутів двох трикутників), отже, точки \(D\) і \(D"\) збігаються.

Зауваження. На малюнку точка \(D\) лежить поза колом, обмеженим колом, описаним біля \(\triangle ABC\) , проте, у разі, коли \(D\) лежить усередині, доказ також залишається вірним.

Теорема

Біля опуклого чотирикутника \(ABCD\) можна описати коло тоді і тільки тоді, коли \(\angle ABD=\angle ACD\) .

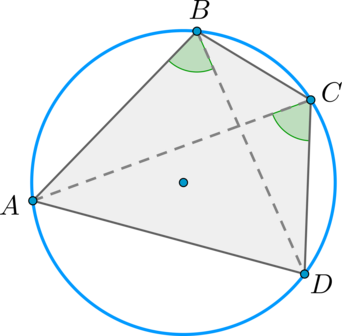
Доведення

Необхідність.Якщо близько \(ABCD\) описана коло, то кути \(\angle ABD\) і \(\angle ACD\) - вписані і спираються на одну дугу \(\buildrel\smile\over(AD)\) , отже, вони рівні.

Достатність.Нехай \(\angle ABD=\angle ACD=\alpha\). Доведемо, що близько (ABCD) можна описати коло.

Опишемо коло близько \(\triangle ABD\) . Нехай пряма \(CD\) перетнула це коло в точці \(C"\) . \(\angle ABD=\angle AC"D \Rightarrow \angle AC"D=\angle ACD\).

Отже, \(\angle CAD=\angle C"AD=180^\circ-\angle ADC-\angle AC"D\), тобто \(\triangle AC"D=\triangle ACD\)по загальній стороні \(AD\) і двом прилеглим кутам (\(\angle C"AD=\angle CAD\) , \(\angle ADC"=\angle ADC\) - загальний). Значить, \(DC"=DC\), тобто точки \(C"\) і \(C\) збігаються.

Теореми

1. Якщо близько паралелограма описано коло, то він – прямокутник (рис. 1).

2. Якщо біля ромба описано коло, то він – квадрат (рис. 2).

3. Якщо біля трапеції описано коло, то воно рівнобедрене (рис. 3).

Вірні і зворотні твердження: біля прямокутника, ромба та рівнобедреної трапеції можна описати коло, і до того ж лише одну.

Доведення

1) Нехай у паралелограма (ABCD) описана коло. Тоді суми його протилежних кутів дорівнюють \(180^\circ: \quad \angle A+\angle C=180^\circ\). Однак у паралелограмі протилежні кути рівні, т.к. \(\angle A=\angle C\) . Отже, \(\angle A=\angle C=90^\circ\). Значить, за визначенням \(ABCD\) - Прямокутник.

2) Нехай біля ромба (MNKP) описана коло. Аналогічно попередньому пункту (бо ромб є паралелограмом) доводиться, що (MNKP) - прямокутник. Але всі сторони цього прямокутника рівні (бо він ромб), значить (MNKP) - квадрат.

Зворотне твердження очевидне.

3) Нехай біля трапеції (QWER) описана коло. Тоді \(\angle Q+\angle E=180^\circ\). Але з визначення трапеції випливає, що \(\angle Q+\angle W=180^\circ\). Отже, \(\angle W=\angle E\) . Т.к. кути при підставі (WE) трапеції рівні, то вона рівнобедрена.

Зворотне твердження очевидне.

Дотримання Вашої конфіденційності є важливим для нас. З цієї причини ми розробили Політику конфіденційності, яка описує, як ми використовуємо та зберігаємо Вашу інформацію. Будь ласка, ознайомтеся з нашими правилами дотримання конфіденційності та повідомте нам, якщо у вас виникнуть будь-які питання.

Збір та використання персональної інформації

Під персональної інформацією розуміються дані, які можна використовувати для ідентифікації певного особи чи зв'язку з ним.

Від вас може бути запитане надання вашої персональної інформації у будь-який момент, коли ви зв'язуєтесь з нами.

Нижче наведено приклади типів персональної інформації, яку ми можемо збирати, і як ми можемо використовувати таку інформацію.

Яку персональну інформацію ми збираємо:

• Коли ви залишаєте заявку на сайті, ми можемо збирати різноманітну інформацію, включаючи ваше ім'я, номер телефону, адресу електронної поштиі т.д.

Як ми використовуємо вашу персональну інформацію:

• Персональна інформація, що збирається нами, дозволяє нам зв'язуватися з вами і повідомляти про унікальні пропозиції, акції та інші заходи та найближчі події.
• Час від часу ми можемо використовувати вашу персональну інформацію для надсилання важливих повідомлень та повідомлень.
• Ми також можемо використовувати персональну інформацію для внутрішніх цілей, таких як проведення аудиту, аналізу даних та різних досліджень з метою покращення послуг, що надаються нами, та надання Вам рекомендацій щодо наших послуг.
• Якщо ви берете участь у розіграші призів, конкурсі або подібному стимулювальному заході, ми можемо використовувати інформацію, що надається, для управління такими програмами.

Розкриття інформації третім особам

Ми не розкриваємо отриману від Вас інформацію третім особам.

Винятки:

• Якщо необхідно - відповідно до закону, судовим порядком, у судовому розгляді, та/або на підставі публічних запитів або запитів від державних органівна території РФ – розкрити вашу персональну інформацію. Ми також можемо розкривати інформацію про вас, якщо ми визначимо, що таке розкриття необхідно чи доречно з метою безпеки, підтримання правопорядку, або інших суспільно важливих випадків.
• У разі реорганізації, злиття або продажу ми можемо передати персональну інформацію, що збирається нами, відповідній третій особі – правонаступнику.

Захист персональної інформації

Ми вживаємо запобіжних заходів - включаючи адміністративні, технічні та фізичні - для захисту вашої персональної інформації від втрати, крадіжки та недобросовісного використання, а також від несанкціонованого доступу, розкриття, зміни та знищення.

Дотримання вашої конфіденційності на рівні компанії

Для того, щоб переконатися, що ваша персональна інформація знаходиться в безпеці, ми доводимо норми дотримання конфіденційності та безпеки до наших співробітників і суворо стежимо за дотриманням заходів дотримання конфіденційності.

>>Геометрія: Коло, описане біля трикутника. Повні уроки

ТЕМА УРОКА: Окружність, описана біля трикутника.

Цілі уроку:

• Поглибити знання на тему «Описані кола в трикутниках»

Завдання уроку:

• Систематизувати знання з цієї теми
• Підготуватись до вирішення завдань підвищеної складності.

План уроку:

1. Вступ.
2. Теоретична частина.
3. Для трикутника.
4. Практична частина.

Вступ.

Тема «Вписані та описані кола в трикутниках» є однією з найскладніших у курсі геометрії. На уроках їй приділяється дуже мало часу.

Геометричні завдання цієї теми включаються до другої частини екзаменаційної роботи ЄДІза курс середньої школи
Для успішного виконання цих завдань необхідні тверді знання основних геометричних фактів та деякий досвід у вирішенні геометричних завдань.

Теоретична частина.

Описане коло багатокутника- Коло, що містить всі вершини багатокутника. Центром є точка (прийнято позначати O) перетину серединних перпендикулярів до сторін багатокутника.

Властивості.

Центр описаного кола опуклого n-кутника лежить у точці перетину серединних перпендикулярів до його сторін. Як наслідок: якщо поряд з n-кутником описано коло, то всі серединні перпендикуляри до його сторін перетинаються в одній точці (центрі кола).
Навколо будь-якого правильного багатокутника можна описати коло.

Для трикутника.

Коло називається описаним біля трикутника, якщо вона проходить через усі його вершини.

Навколо будь-якого трикутника можна описати коло, до того ж тільки одну. Її центром буде точка перетину серединних перпендикулярів.

У гострокутного трикутника центр описаного кола лежить всередині, у тупокутного - поза трикутником, У прямокутного - на середині гіпотенузи.

Радіус описаного кола може бути знайдений за формулами:

Де:
a, b, c- Сторони трикутника,
α - Кут, що лежить проти сторони a,
S- площа трикутника.

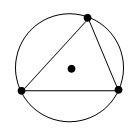
Довести:

т.о - точка перетину серединних перпендикулярів до сторін ABC

Доведення:

1. ΔAОC - рівнобедрений, т.к. ОА = ОС (як радіуси)
2. ΔAОC - рівнобедрений, перпендикуляр OD - медіана та висота, тобто. т.про лежить на серединному перпендикулярі до сторони АС
3. Аналогічно доводиться, що лежить на серединних перпендикулярах до сторін АВ і ВС

Що й потрібно було довести.

Зауваження.

Пряму, що проходить через середину відрізка перпендикулярно до нього, часто називають серединним перпендикуляром. У зв'язку з цим іноді говорять, що центр кола, описаного біля трикутника, лежить на перетині серединних перпендикулярів до сторін трикутника.