Паралелограмом називається чотирикутник, у якого протилежні сторонипаралельні, тобто. лежать на паралельних прямих

Властивості паралелограма: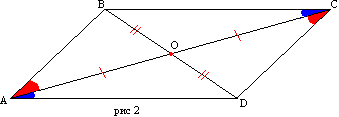
Теорема 22. Протилежні сторони паралелограма рівні.
Доведення. У паралелограмі АВСD проведемо діагональ АС. Трикутники АСD та АСВ рівні, як мають спільну сторону АС та дві пари рівних кутів. прилеглих до неї: ∠ САВ = ∠ АСD, ∠ АСВ = ∠ DAC (як навхрест лежачі кути при паралельних прямих AD і ВС). Отже, АВ=CD та ВС=AD, як відповідні сторони рівних трикутників, ч.т.д. З рівності цих трикутників також випливає рівність відповідних кутів трикутників:
Теорема 23. Протилежні кути паралелограма дорівнюють: ∠ А = ∠ С і ∠ В = ∠ D.
Рівність першої пари йде з рівності трикутників АВD та CBD, а другої – АВС та ACD.
Теорема 24. Сусідні кути паралелограма, тобто. кути, що прилягають до одного боку, становлять у сумі 180 градусів.
Це так, тому що вони є односторонніми внутрішніми кутами.
Теорема 25. Діагоналі паралелограма ділять один одного в точці їхнього перетину навпіл.
Доведення. Розглянемо трикутники ВОС та АОD. За першою властивістю AD=ВС ∠ ОАD=∠ ОСВ і ∠ ОDА=∠ ОВС як навхрест, що лежать при паралельних прямих AD і ВС. Тому трикутники ВОС і АОD рівні по стороні і кутам, що прилягають до неї. Отже, ВО=ОD і АО=ОС, як відповідні сторони рівних трикутників, т.д.

Ознаки паралелограма
Теорема 26. Якщо протилежні сторони чотирикутника попарно рівні, він є паралелограмом.
Доведення. Нехай у чотирикутника АВСD сторони AD і ВС, АВ та CD відповідно рівні (рис2). Проведемо діагональ АС. Трикутник АВС і ACD рівні по трьох сторонах. Тоді кути ВАС та DСА рівні і, отже, АВ паралельна CD. Паралельність сторін ЗС і AD випливає з рівності кутів CAD та АСВ.
Теорема 27. Якщо протилежні кути чотирикутника попарно рівні, він є паралелограмом.
Нехай ∠ А = ∠ С і ∠ В = ∠ D. Т.к. ∠ А+∠ В+∠ С+∠ D=360 про, то ∠ А+∠ В=180 про сторони AD і ВС паралельні (за ознакою паралельності прямих). Також доведемо і паралельність сторін АВ і CD і зробимо висновок, що АВСD є паралелограмом за визначенням.
Теорема 28. Якщо сусідні кути чотирикутника, тобто. кути, прилеглі до однієї стороні, становлять у сумі 180 градусів, він є паралелограмом.
Якщо внутрішні односторонні кути у сумі становлять 180 градусів, то прямі пралельні. Значить АВ парал CD і НД парал AD. Чотирьохкутник виявляється паралелограмом за визначенням.
Теорема 29. Якщо діагоналі чотирикутника взаємно діляться у точці перетину навпіл, то чотирикутник – паралелограм.
Доведення. Якщо АО=ОС, ВО=ОD, то трикутники АOD і ВОС рівні, що мають рівні кути (вертикальні) при вершині О, укладені між парами рівних сторін. З рівності трикутників укладаємо, що і ВС рівні. Також рівні сторони АВ та CD, і чотирикутник виявляється паралелограмом за ознакою 1.
Теорема 30. Якщо чотирикутник має пару рівних, паралельних між собою сторін, він є паралелограмом.
Нехай у чотирикутнику АВСD сторони АВ і CD паралельні та рівні. Проведемо діагоналі АС та ВD. З паралельності цих прямих випливає рівність навхрест лежачих кутів АВО=СDО і ВАО=ОСD. Трикутники АВО і СДО рівні по стороні і кутам, що прилягають до неї. Тому АТ = ОС, ВО = ОD, тобто. діагоналі точкою перетину діляться навпіл і чотирикутник виявляється паралелограмом за ознакою 4.

У геометрії розглядають окремі випадки паралелограма.

1. Визначення паралелограма.

Якщо пару паралельних прямих перетнемо іншою парою паралельних прямих, то отримаємо чотирикутник, у якого протилежні сторони попарно паралельні.

У чотирикутниках ABDС та ЕFNМ (рис. 224) ВD || АС та AB || CD;

ЕF || МN та ЕМ || FN.

Чотирьохкутник, у якого протилежні сторони попарно паралельні, називається паралелограмом.

2. Властивості паралелограма.

Теорема. Діагональ паралелограма ділить його на два рівні трикутники.

Нехай є паралелограм ABDС (рис. 225), в якому AB | СD та АС || ВD.

Потрібно довести, що діагональ ділить його на два рівні трикутники.

Проведемо в паралелограмі ABDС діагональ СВ. Доведемо, що \(\Delta\)CAB = \(\Delta\)СDВ.

Сторона СВ загальна цих трикутників; ∠ABC = ∠BCD, як внутрішні навхрест лежачі кути при паралельних AB і СD та січній СВ; ∠ACB = ∠СВD, теж як внутрішні навхрест лежачі кути при паралельних АС і ВD і січній CB.

Звідси \(\Delta\)CAB = \(\Delta\)СDВ.

Таким же шляхом можна довести, що діагональ AD розділить паралелограм на два рівні трикутники АСD і ABD.

Наслідки:

1 . Протилежні кути паралелограма рівні між собою.

∠А = ∠D, це випливає з рівності трикутників CAB та СDВ.

Аналогічно і ∠С = ∠В.

2. Протилежні сторони паралелограма рівні між собою.

AB = СD та АС = ВD, оскільки це сторони рівних трикутників і лежать проти рівних кутів.

Теорема 2. Діагоналі паралелограма у точці їх перетину діляться навпіл.

Нехай BC та AD - діагоналі паралелограма AВDС (рис. 226). Доведемо, що АТ = OD та СО = OB.

Для цього порівняємо якусь пару протилежно розташованих трикутників, наприклад \(\Delta\)AOB і \(\Delta\)СОD.

У цих трикутниках AB = СD як протилежні сторони паралелограма;

∠1 = ∠2, як кути внутрішні навхрест лежать при паралельних AB і СD та січній AD;

∠3 = ∠4 з тієї ж причини, тому що AB || СD і СВ – їх січуча.

Звідси випливає, що \(\Delta\)AOB = \(\Delta\)СОD. На рівних трикутниках проти рівних кутів лежать рівні сторони. Отже, АТ = OD та СО = OB.

Теорема 3. Сума кутів, що прилягають до однієї сторони паралелограма, дорівнює 180 °.

У паралелограмі ABCD проведемо діагональ АС і отримаємо два трикутники ABC та ADC.

Трикутники рівні, оскільки ∠1 = ∠4, ∠2 = ∠3 (нахрест лежачі кути при паралельних прямих), а сторона АС загальна.
З рівності \(\Delta\)ABC = \(\Delta\)ADC випливає, що AB = CD, BC = AD, ∠B = ∠D.

Сума кутів, що прилягають до однієї сторони, наприклад, кутів А і D, дорівнює 180° як односторонніх при паралельних прямих.

Паралелограм – це чотирикутник, у якого протилежні сторони попарно паралельні. На наступному малюнку представлено паралелограм ABCD. У нього сторона AB паралельна стороні CD, а сторона BC паралельна стороні AD.

Як ви вже встигли здогадатися, паралелограм є опуклим чотирикутником. Розглянемо основні властивості паралелограма.

Властивості паралелограма

1. У паралелограмі протилежні кути та протилежні сторони рівні. Доведемо цю властивість – розглянемо паралелограм, поданий на наступному малюнку.

Діагональ BD поділяє його на два рівні трикутники: ABD і CBD. Вони рівні по стороні BD і двом кутам, що прилягають до неї, так як кути навхрест лежать при січній BD паралельних прямих BC і AD і AB і CD відповідно. Отже, AB = CD та
BC = AD. А з рівності кутів 1, 2, 3 і 4 випливає, що кут A = кут1 + кут3 = кут2 + кут4 = кут С.

2. Діагоналі паралелограма точкою перетину діляться навпіл. Нехай точка О є точка перетину діагоналей AC та BD паралелограма ABCD.

Тоді трикутник AOB і трикутник COD рівні між собою, по стороні та двом прилеглим до неї кутам. (AB=CD так як це протилежні сторони паралелограма. А кут1 = кут2 і кут3 = кут4 як навхрест кути, що лежать при перетині прямих AB і CD січними AC і BD відповідно.) З цього випливає, що AO = OC і OB = OD, що і потрібно було довести.

Усі основні властивості проілюстровані наступних трьох малюнках.

Конспект уроку.

Алгебра 8 клас

Вчитель Сисий А.К.

Школа 1828

Тема уроку: «Паралелограм та його властивості»

Тип уроку: комбінований

Цілі уроку:

1) Забезпечити засвоєння нового поняття – паралелограм та його властивостей

2) Продовжити розвиток навичок та умінь вирішення геометричних завдань;

3) Розвиток культури математичної мови

План уроку:

1. Організаційний момент

(Слайд 1)

На слайді демонструється висловлювання Льюїса Керролла. Учням повідомляється про мету уроку. Перевіряється готовність учнів до уроку.

2. Актуалізація знань

(Слайд 2)

На дошці - завдання для усної роботи. Вчитель пропонує учням подумати над цими завданнями та підняти руку тим, хто зрозумів, як завдання вирішувати. Після вирішення двох завдань, на доказ теореми про суму кутів викликається до дошки учень, який самостійно робить додаткові побудови на кресленні та доводить усно теорему.

Учнями використовується формула суми кутів багатокутника:

3. Основна частина

(Слайд 3)

На дошці визначення паралелограма. Вчитель говорить про нову фігуру та формулює визначення, роблячи за допомогою креслення необхідні пояснення. Потім на картатій частині презентації, за допомогою маркера та лінійки, показує, як можна малювати паралелограм (можливо кілька випадків)

(Слайд 4)

Вчитель формулює першу властивість паралелограма. Пропонує учням сказати, на малюнку, що дано і що необхідно довести. Після цього на дошці з'являється завдання. Учні здогадуються (можливо за допомогою вчителя), що шукані рівності треба довести через рівності трикутників, які можна отримати, провівши діагональ (на дошці з'являється діагональ). Далі учні здогадуються, чому трикутники рівні і називають ознаку рівності трикутників (з'являється відповідна форма). Усно повідомляють факти, які необхідні рівності трикутників (у міру того як вони їх називають, з'являється відповідна візуалізація). Далі учні формулюють властивість рівних трикутників, воно з'являється у вигляді пункту 3 докази, а потім самостійно завершують доказ теореми усно.

(Слайд 5)

Вчитель формулює другу властивість паралелограма. На дошці з'являється малюнок паралелограма. Вчитель пропонує за малюнком сказати, що дано, що необхідно довести. Після того, як учні правильно повідомляють про те, що дано і що необхідно довести, з'являється умова теореми. Учні здогадуються, що рівність частин діагоналей можна довести через рівність трикутниківAOBі COD. За допомогою попередньої властивості паралелограма здогадуються про рівність сторінABі CD. Потім розуміють, що треба знайти рівні кути і за допомогою властивостей паралельних прямих доводять рівність кутів, що прилягають до рівних сторін. Ці етапи візуалізуються на слайді. З рівності трикутників випливає і істинність теореми – промовляють учні на слайді з'являється відповідна візуалізація.

(Слайд 6)

Вчитель формулює третю властивість паралелограма. Залежно від часу, що залишається до кінця уроку, вчитель може дати можливість учням самостійно довести цю властивість, або обмежиться його формулюванням, а сам доказ залишити учням як домашню роботу. Доказ може спиратися на суму кутів вписаного багатокутника, яка повторювалася на початку уроку, або на суму односторонніх внутрішніх кутів при двох паралельних прямихADі BC, і січеною, наприкладAB.

4. Закріплення матеріалу

У цьому етапі учні, використовуючи раніше вивчені теореми, вирішують завдання. Ідеї ​​вирішення завдання підбирають учні самостійно. Так як можливих варіантівоформлення чимало і всі вони залежать від того, яким чином учні шукатимуть рішення задачі, візуалізації розв'язання задач немає, а учні самостійно оформлюють кожен етап рішення на окремій дошці із записом рішення у зошит.

(Слайд 7)

З'являється умова завдання. Вчитель пропонує за умовою сформулювати "Дано". Після того, як учні, правильно складуть короткий запис умови на дошці з'являється «Дано». Хід розв'язання задачі може виглядати так:

Проведемо висоту BH (візуалізовано)

Трикутник AHB – прямокутний. Кут A дорівнює куту C і дорівнює 30 0 (за властивістю про протилежні кути в паралелограмі). 2BH =AB (за властивістю катета, що лежить навпроти кута 30 0 у прямокутному трикутнику). Отже AB = 13 див.

AB = CD, BC = AD (за якістю протилежних сторін у паралелограмі) Значить AB = CD = 13см. Так як периметр паралелограма дорівнює 50 см, то BC = AD = (50 - 26): 2 = 12см.

Відповідь: AB = CD = 13 см; BC = AD = 12 см.

(Слайд 8)

З'являється умова завдання. Вчитель пропонує за умовою сформулювати "Дано". Після цього з'являється «Дано» на екрані. За допомогою червоних ліній виділяється чотирикутник, про який необхідно довести, що він паралелограм. Хід розв'язання задачі може виглядати так:

Т.к. BK та MD перпендикуляри до однієї прямої, то прямі BK та MD паралельні.

Через суміжні кути можна показати, що сума внутрішніх односторонніх кутів при прямих BM та KD та січній MD дорівнює 180 0 . Тому дані прямі паралельні.

Оскільки чотирикутник BMDK протилежні сторони попарно паралельні, то даний чотирикутник паралелограм.

5. Закінчення уроку. Поведінка підсумків.

(Слайд 8)

На слайді постають питання з нової теми, куди учні відповідають.