Если на плоскости последовательно начертить несколько отрезков так, чтобы каждый следующий начинался в том месте, где закончился предыдущий, то получится ломаная линия. Эти отрезки называют звеньями, а места их пересечения — вершинами. Когда конец последнего отрезка пересечется с начальной точкой первого, то получится замкнутая ломаная линия, делящая плоскость на две части. Одна из них является конечной, а вторая бесконечной.

Простая замкнутая линия вместе с заключенной в ней частью плоскости (той, которая конечна) называют многоугольником. Отрезки являются сторонами, а образованные ими углы — вершинами. Количество сторон любого многоугольника равно числу его вершин. Фигура, которая имеет три стороны, называется треугольником, а четыре — четырехугольником. Многоугольник численно характеризуется такой величиной, как площадь, которая показывает размер фигуры. Как найти площадь четырехугольника? Этому учит раздел математики — геометрия.

Чтобы найти площадь четырехугольника, нужно знать к какому типу он относится - выпуклому или невыпуклому? весь лежит относительно прямой (а она обязательно содержит какую-либо из его сторон) по одну сторону. Кроме того, есть и такие виды четырехугольников, как параллелограмм с попарно равными и параллельными противоположными сторонами (разновидности его: прямоугольник с прямыми углами, ромб с равными сторонами, квадрат со всеми прямыми углами и четырьмя равными сторонами), трапеция с двумя параллельными противоположными сторонами и дельтоид с двумя парами смежных сторон, которые равны.

Площади любого многоугольника находят, применяя общий метод, который заключается в том, чтобы разбить его на треугольники, для каждого вычислить площадь произвольного треугольника и сложить полученные результаты. Любой выпуклый четырехугольник делится на два треугольника, невыпуклый — на два или три его в этом случае может складываться из суммы и разности результатов. Площадь любого треугольника вычисляют как половину произведения основания (a) на высоту (ħ), проведенную к основанию. Формула, которая применяется в этом случае для вычисления, записывается как: S = ½ . a . ħ.

Как найти площадь четырехугольника, например, параллелограмма? Нужно знать длину основания (a), длину боковой стороны (ƀ) и найти синус угла α, образованного основанием и боковой стороной (sinα), формула для расчета будет выглядеть: S = a . ƀ . sinα. Так как синус угла α есть произведение основания параллелограмма на его высоту (ħ = ƀ) — линию перпендикулярная основанию, то его площадь вычисляют, умножив на высоту его основание: S = a . ħ. Для расчета площади ромба и прямоугольника также подходит эта формула. Так как у прямоугольника боковая сторона ƀ совпадает с высотой ħ, то его площадь вычисляют по формуле S = a . ƀ. потому что a = ƀ, будет равняться квадрату его стороны: S = a . a = a². вычисляется как половина суммы его сторон, умноженная на высоту (она проводится к основанию трапеции перпендикулярно): S = ½ . (a + ƀ) . ħ.

Как найти площадь четырехугольника, если неизвестны длины его сторон, но известны его диагонали (e) и (f), а также синус угла α? В этом случай площадь вычисляют, как половину произведения его диагоналей (линии, которые соединяют вершины многоугольника), умноженное на синус угла α. Формула может быть записана в таком виде: S = ½ . (e . f) . sinα. В частности в этом случае будет равняться половине произведения диагоналей (линии, соединяющие противоположные углы ромба): S = ½ . (e . f).

Как найти площадь четырехугольника, который не является параллелограммом или трапецией, его обычно принято называть произвольный четырехугольник. Площадь такой фигуры выражают через его полупериметр (Ρ — сумма двух сторон с общей вершиной), стороны a, ƀ, c, d и сумму двух противоположных углов (α + β): S = √[(Ρ - a) . (Ρ - ƀ) . (Ρ - c) . (Ρ - d) - a . ƀ . c . d . cos² ½ (α + β)].

Если четырехугольник вписан в окружность, а φ = 180о, то для расчета его площади используют формулу Брахмагупты (индийский астроном и математик, живший в 6—7 веках нашей эры): S = √[(Ρ - a) . (Ρ - ƀ) . (Ρ - c) . (Ρ - d)]. Если четырехугольник описан окружностью, то (a + c = ƀ + d), а его площадь вычисляют: S = √[ a . ƀ . c . d] . sin ½ (α + β). Если четырехугольник одновременно является описанным одной окружностью и вписанным в другую окружность, то для вычисления площади используют следующую формулу: S = √.

Четырехугольником называется фигура, состоящая из четырех вершин, три из которых не лежат на одной прямой, и отрезков, соединяющих их.

Существует множество четырехугольников. К ним относятся параллелограммы, квадраты, ромбы, трапеции. Найти можно найти по сторонам, легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ. Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:

Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.

Пусть дан четырехугольник с двумя диагоналями d1 =5 см;d2 =4см. Острый угол между ними равен α = 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий. Подставим данные:

На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет .

Площадь четырехугольника по сторонам

Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так:
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:

Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см. Для начала найдем полупериметр:

используем найденное значение для расчета площади:

Площадь четырехугольника, заданного координатами

Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY .

Определение .

Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник.

Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности?

Теорема 1 .

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны .

В четырехугольник ABCD можно вписать окружность, если

И обратно, если суммы противоположных сторон четырехугольника равны:

то в четырехугольник ABCD можно вписать окружность.

Теорема 2 .

Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис .

O — точка пересечения биссектрис четырехугольника ABCD.

AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD,

то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.

3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.

AM=AN,

5. Площадь четырехугольника связана с радиусом вписанной в него окружности формулой

При решении планиметрических заданий курса геометрии нередко встречается фигура с 4-мя сторонами. Да, речь идет о четырехугольнике. Произвольный многоугольник с четырьмя углами встречается реже, чем его частные случаи, – трапеции, дельтоиды, параллелограммы. В последнюю «группу» входят также ромбы, прямоугольники, квадраты.
Рассмотрим, какие данные фигуры необходимо знать, чтобы рассчитать ее площадь.

Как найти площадь четырехугольника

Многоугольник произвольный

Для нахождения его площади вам потребуются диагонали фигуры, а также угол, полученный как результат их пересечения.

• S = (d1*d2*sinα)/2,
• d1, d2 – диагонали,
• α – угол, полученный путем их пересечения.

Многоугольник в окружности

Если заданный четырехугольник помещен в окружность, известна длина сторон фигуры, то в определении площади многоугольника поможет соотношение:

S = √(p – m)(p – k)(p – l)(p – e), p = (m + k + l + e)/2.
m, k, l, e – его стороны.

Как найти площадь четырехугольника — трапеции

Данную фигуру отличает наличие параллельных 2-ух сторон. Чтобы определить площадь такого многоугольника воспользуйтесь такими параметрами:

• Если известны величины параллельных сторон и перпендикуляра-высоты, проведенной к ним, площадь вычисляется с помощью выражения S = ((a + b)*h)/2,
  a и b – основания,
  h – перпендикуляр-высота.
• Исходя из определения линии средины (k = (a + b)/2)), предыдущая формула приобретет следующий вид: S = k*h,
  k – линия средины.
  Известные диагонали трапеции и градусная мера угла, образованная в результате их пересечения, также помогут определить площадь фигуры: S = (d1*d2*sinβ)/2,
  d1, d2 – диагонали,
  β – угол, полученный путем их пересечения.
• Заданы 4 стороны: S = ((m + l)√k 2 – ((m – l) 2 + k 2 – d 2) 2 /(4(m – l) 2))/2,
  m, l — стороны параллельные,
  k, d — стороны боковые.

Как найти площадь четырехугольника — дельтоида

Многоугольник-дельтоид характеризуется наличием 2-ух пар равных сторон. Вычислить площадь такого четырехугольника рассчитывается следующим образом:

• Известны стороны фигуры и угол, образованный сторонами разной длины:
  S = m*l*sinϕ,
  m, l – стороны дельтоида,
  ϕ – угол между ними.
• Известны стороны фигуры и углы, образованные сторонами равной длины:
  S = m 2 *sinα/2 + l 2 *sinβ/2,
  m, l – стороны дельтоида,
  α, β — углы между равными сторонами.
• Наличие известных диагоналей также позволяет определить площадь фигуры:
  S = d1*d2/2,
  d1, d2 – диагонали дельтоида.
• Если в фигуру вписана окружность, то знание ее радиуса позволяет вычислить площадь дельтоида: S = (m + l)*r,
  m, l – стороны дельтоида,
  r – радиус в случае вписанной окружности.

Как найти площадь четырехугольника — параллелограмма

Если выпуклый многоугольник имеет 2 пары непересекающихся сторон, то перед вами – параллелограмм.

Общее выражение

Для определения площади данного вида фигуры потребуются:

• Сторона четырехугольника и высота, на нее опущенная: S = k*h(k),
  k – сторона фигуры,
  h(k) – высота к ней.
• Длина двух сторон, имеющих одну вершину, и градусная мера угла при данной вершине:
  S = l*k*sinϕ,
  k, l – стороны многоугольника,
  ϕ – угол между ними.
• Диагонали фигуры и угол, полученный как результат их пересечения: S = d1*d2*sinβ/2,
  d1, d2 – диагонали,
  β – угол — результат их пересечения.

Ромб

Данный четырехугольник – частный случай параллелограмма, имеющий 4 равные стороны. Поэтому выражения, справедливые для параллелограмма, верны и для него. Тогда

• S = k*h(k),
  k – сторона фигуры, h(k) – высота к ней.
• S = k 2 *sinϕ,
  k – сторона четырехугольника, ϕ – угол между сторонами.
• S = d1*d2/2 (т.к. диагонали фигуры при пересечении образую прямой угол, а sin90° = 1),
  d1, d2 – диагонали многоугольника.

Прямоугольник

Такой многоугольник имеет 2 пары равных сторон, а градусная мера его углов – 90°. Для нахождения его площади справедливы следующие выражения:

• S = k*l,
  k, l – стороны фигуры.
• S = d 2 *sinβ/2,
  d – диагонали четырехугольника, β – угол – результат их пересечения.
• S = 2R 2 *sinβ,
  R – радиус в случае описанной окружности.

Квадрат

В данном случае у соотношения, полученные на предыдущем этапе, приобретут следующий вид (т.к. стороны такого вида прямоугольника равны):

• S = k 2 , k – сторона фигуры.

• S = d 2 /2, d – диагональ квадрата.

• S = 2R 2 , R – радиус в случае описанной окружности.
• S = 4r 4 , r – радиус в случае вписанной окружности.

Теорема 1. Площадь трапеции равна произведению полусуммы ее оснований на высоту:

Теорема 2. Диагонали трапеции делят ее на четыре треугольника, два из которых подобны, а два другие имеют одинаковую площадь:

Теорема 3. Площадь параллелограмма равна произведению основания на высоту, опущенную на данное основание, или произведению двух сторон на синус угла между ними:

Теорема 4. В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон:

Теорема 5. Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:

Теорема 6. Площадь четырехугольника, описанного около окружности, равна произведению полупериметра этого четырехугольника на радиус данной окружности: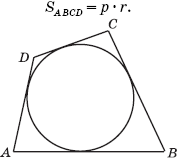

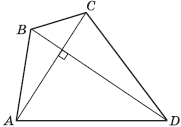
Теорема 7. Четырехугольник, вершинами которого являются середины сторон произвольного выпуклого четырехугольника, есть параллелограмм, площадь которого равна половине площади исходного четырехугольника:

Теорема 8. Если у выпуклого четырехугольника диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:

AB2 + CD2 = BC2 + AD2 .

Статья опубликована при поддержке компании "ДКРОСТ". Горки детские , домики, песочницы и многое другое - изготовление и продажа детских площадок оптом и в розницу. Самые низкие цены, скидки, сжатые сроки изготовления, выезд и консультация специалиста, гарантия качества. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты Вы сможете на сайте, который располагается по адресу: http://dkrost.ru/.

Доказательства некоторых теорем

Доказательство теоремы 2 . Пусть ABCD - данная трапеция, AD и BC - ее основания, O - точка пересечения диагоналей AC и BD этой трапеции. Докажем, что треугольники AOB и COD имеют одинаковую площадь. Для этого опустим из точек B и C на прямую AD перпендикуляры BP и CQ. Тогда площадь треугольника ABD равна

А площадь треугольника ACD равна

Так как BP = CQ, то и S∆ABD = S∆ACD . Но площадь треугольника AOB есть разность площадей тре­угольников ABD и AOD, а площадь треугольника COD - разность площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, что и требовалось доказать.

Доказательство теоремы 4 . Пусть ABCD - параллелограмм, AB = CD = a , AD = BC = b,
AC = d1 , BD = d2 , ∠BAD = α, ∠ADC = 180° – α. Применим к треугольнику ABD теорему косинусов:

Применив теперь теорему косинусов к тре­угольнику ACD, получим:

Складывая почленно полученные равенства, получаем, что что и требовалось доказать.

Доказательство теоремы 5. Пусть ABCD - произвольный выпуклый четырехугольник, E - точка пересечения его диагоналей, AE = a , BE = b,
CE = c, DE = d, ∠AEB = ∠CED = ϕ, ∠BEC =
= ∠AED = 180° – ϕ. Имеем:

что и требовалось доказать.

Доказательство теоремы 6 . Пусть ABCD - произвольный четырехугольник, описанный около окружности, O - центр этой окружности, OK, OL, OM и ON - перпендикуляры, опущенные из точки O на прямые AB, BC, CD и AD соответственно. Имеем: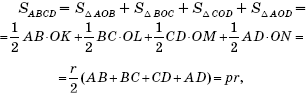

где r - радиус окружности, а p - полупериметр четырехугольника ABCD.

Доказательство теоремы 7 . Пусть ABCD - произвольный выпуклый четырехугольник, K, L, M и N - середины сторон AB, BC, CD и AD соответственно. Так как KL - средняя линия треугольника ABC, то прямая KL параллельна прямой AC и Аналогично, прямая MN параллельна прямой AC и Следовательно, KLMN - параллелограмм. Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD. Следовательно,

Аналогично,

Это значит, что

откуда вытекает, что

Доказательство теоремы 8 . Пусть ABCD - произвольный выпуклый четырехугольник, у которого диагонали взаимно перпендикулярны, пусть E - точка пересечения его диагоналей,
AE = a , BE = b, CE = c, DE = d. Применим к тре­угольникам ABE и CDE теорему Пифагора:
AB2 = AE2 + BE2 = a 2 + b2 ,
CD2 = CE2 + DE2 = c2 + d2 ,
следовательно,
AB2 + CD2 = a 2 + b2 + c2 + d2 .
Применив теперь теорему Пифагора к треугольникам ADE и BCE, получим:
AD2 = AE2 + DE2 = a 2 + d2 ,
BC2 = BE2 + CE2 = b2 + c2 ,
откуда вытекает, что
AD2 + BC2 = a 2 + b2 + c2 + d2 .
Значит, AB2 + CD2 = AD2 + BC2 , что и требовалось доказать.

Решения задач

Задача 1 . Около круга описана трапеция с углами при основании α и β. Найти отношение площади трапеции к площади круга.

Решение . Пусть ABCD - данная трапеция, AB и CD - ее основания, DK и CM - перпендикуляры, опущенные из точек C и D на прямую AB. Искомое отношение не зависит от радиуса круга. Поэтому будем считать, что радиус равен 1. Тогда площадь круга равна π, найдем площадь трапеции. Так как треугольник ADK прямоугольный, то

Аналогично, из прямоугольного треугольника BCM находим, что Поскольку в данную трапецию можно вписать окружность, то суммы противоположных сторон равны:
AB + CD = AD + BC,
откуда находим

Значит, площадь трапеции есть

и искомое отношение равно
Ответ :

Задача 2 . В выпуклом четырехугольнике ABCD угол A равен 90°, а угол C не превосходит 90°. Из вершин B и D на диагональ AC опущены перпендикуляры BE и DF. Известно, что AE = CF. Доказать, что угол C прямой.

Доказательство . Так как угол A равен 90°,
а угол C не превосходит 90°, то точки E и F лежат на диагонали AC. Без ограничения общности мы можем считать, что AE < AF (в противном случае следует повторить все нижеследующие рассуждения с заменой точек B и D). Пусть ∠ABE = α,
∠EBC = β, ∠FDA = γ, ∠FDC = δ. Нам достаточно доказать, что α + β + γ + δ = π. Так как

откуда получаем, что что и требовалось доказать.

Задача 3 . Периметр равнобочной трапеции, описанной около круга, равен p. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен α.
Решение . Пусть ABCD - данная равнобочная трапеция с основаниями AD и BC, пусть BH - высота этой трапеции, опущенная из вершины B.
Так как в данную трапецию можно вписать окружность, то

Следовательно,

Из прямоугольного треугольника ABH находим,

Ответ :

Задача 4 . Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD - в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность. Найти отношение площадей треугольника BKC и трапеции ABCD.

Решение . Как известно, для произвольной трапеции прямая, соединяющая точку пересечения диагоналей и точку пересечения продолжений боковых сторон, делит каждое из оснований пополам. Итак, BM = MC и AN = ND. Далее, так как в трапеции ABMN и NMCD можно вписать окружность, то
BM + AN = AB + MN,
MC + ND = CD + MN.
Отсюда следует, что AB = CD, то есть трапеция ABCD - равнобокая. Искомое отношение площадей не зависит от масштаба, поэтому мы можем принять, что KN = x, KM = 1. Из прямоугольных треугольников AKN и BKM получаем, что Записывая вновь уже использованное выше соотношение
BM + AN = AB + MN ⇔

Нам требуется вычислить отношение:

Здесь мы использовали тот факт, что площади треугольников AKD и BKC относятся как квадраты сторон KN и KM, то есть как x2.

Ответ:

Задача 5. В выпуклом четырехугольнике ABCD точки E, F, H, G являются серединами сторон AB, BC, CD, DA соответственно и O - точка пересечения отрезков EH и FG. Известно, что EH = a , FG = b, Найти длины диагоналей четырехугольника.. Пусть ABCD - данная трапеция, AB = 3 и CD = 5 - ее боковые стороны, точки K и M - середины сторон AB и CD соответственно. Пусть, для определенности, AD > BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Так как KM - средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:

Далее, так как в трапецию ABCD можно вписать окружность, то AD + BC = AB + CD = 8. Тогда KM = 4 как средняя линия трапеции ABCD. Пусть BC = x, тогда AD = 8 – x. Имеем:
Значит, BC = 1 и AD = 7.

Ответ: 1 и 7.

Задача 7 . Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали AC равна a , а длина боковой стороны BC равна b. Найти площадь трапеции.

Решение . Пусть E - точка пересечения продолжений боковых сторон трапеции и CD = x, тогда AD = x, AB = 2x. Отрезок CD параллелен отрезку AB и вдвое его короче, значит, CD является средней линией треугольника ABE. Следовательно, CE = BC = b и DE = AD = x, откуда AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC - его медиана. Поэтому AC является и высотой этого треугольника, и значит,

Так как треугольник DEC подобен треугольнику AEB с коэффициентом подобия то AB + CD = 8. Продлим боковые стороны DA и CB до пересечения в точке E. Рассмотрим треугольник ABE, в котором ∠EAB = 50°. ∠EBA = 40°,
следовательно, ∠AEB = 90°. Медиана EM этого треугольника, проведенная из вершины прямого угла, равна половине гипотенузы: EM = AM. Пусть EM = x, тогда AM = x, DN = 4 – x. Согласно условию задачи MN = 1, следовательно,
EN = x + 1. Из подобия треугольников AEM и DEN имеем:

Это означает, что AB = 3 и CD = 5.

Ответ : 3 и 5.

Задача 10 . Выпуклый четырехугольник ABCD описан около окружности с центром в точке O, при этом AO = OC = 1, BO = OD = 2. Найти периметр четырехугольника ABCD.

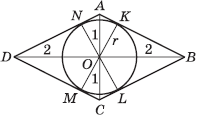
Решение . Пусть K, L, M, N - точки касания окружности со сторонами AB, BC, CD, DA соответственно, r - радиус окружности. Так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания, то тре­угольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO - прямоугольные. Применив к этим треугольникам теорему Пифагора, получим, что

Следовательно, AB = BC = CD = DA, то есть ABCD - ромб. Диагонали ромба перпендикулярны друг другу, и точка их пересечения является центром вписанной окружности. Отсюда легко находим, что сторона ромба равна и значит, периметр ромба равен

Ответ :

Задачи для самостоятельного решения

С-1. Около окружности радиуса r описана равнобочная трапеция ABCD. Пусть E и K - точки касания этой окружности с боковыми сторонами трапеции. Угол между основанием AB и боковой стороной AD трапеции равен 60°. Докажите, что EK параллелен AB, и найдите площадь трапеции ABEK.
С-2. В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции.
С-3 . Можно ли вокруг четырехугольника ABCD описать окружность, если ∠ADC = 30°, AB = 3, BC = 4, AC = 6?
С-4. В трапеции ABCD (AB - основание) величины углов DAB, BCD, ADC, ABD и ADB образуют арифметическую прогрессию (в том порядке, в котором они написаны). Найдите расстояние от вершины C до диагонали BD, если высота трапеции равна h.
С-5. Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность. Отношение высоты трапеции к радиусу описанной окружности равно Найдите углы трапеции.
С-6. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка O так, что OB = OD = 13. Найдите расстояние от точки O до наиболее удаленной от нее вершины прямоугольника.
С-7. Периметр параллелограмма ABCD равен 26. Величина угла ABC равна 120°. Радиус окружности, вписанной в треугольник BCD, равен Найдите длины сторон параллелограмма, если известно, что AD > AB.
С-8. Четырехугольник ABCD вписан в окружность с центром в точке O. Радиус OA перпендикулярен радиусу OB, а радиус OC перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки C на прямую AD, равна 9. Длина отрезка BC в два раза меньше длины отрезка AD. Найдите площадь треугольника AOB.
С-9. В выпуклом четырехугольнике ABCD вершины A и C противоположны, а длина стороны AB равна 3. Угол ABC равен угол BCD равен Найдите длину стороны AD, если известно, что площадь четырехугольника равна

С-10. В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. Известно, что
AD = 2, ∠ABD = ∠ACD = 90°, и расстояние между точкой пересечения биссектрис треугольника ABD и точкой пересечения биссектрис треугольника ACD равно Найдите длину стороны BC.
С-11. Пусть M - точка пересечения диагоналей выпуклого четырехугольника ABCD, в котором стороны AB, AD и BC равны между собой. Найдите угол CMD, если известно, что DM = MC,
а ∠CAB ≠ ∠DBA.
С-12. В четырехугольнике ABCD известно, что ∠A = 74°, ∠D = 120°. Найдите угол между биссектрисами углов B и C.
С-13. В четырехугольник ABCD можно вписать окружность. Пусть K - точка пересечения его диагоналей. Известно, что AB > BC > KC, а периметр и площадь треугольника BKC равны соответственно 14 и 7. Найдите DC.
С-14. В трапеции, описанной около окружности, известно, что BC AD, AB = CD, ∠BAD =
= 45°. Найдите AB, если площадь трапеции ABCD равна 10.
С-15. В трапеции ABCD с основаниями AB и CD известно, что ∠CAB = 2∠DBA. Найдите площадь трапеции.
С-16. В параллелограмме ABCD известно, что AC = a , ∠CAB = 60°. Найдите площадь параллелограмма.
С-17 . В четырехугольнике ABCD диагонали AC и BD пересекаются в точке K. Точки L и M являются соответственно серединами сторон BC и AD. Отрезок LM содержит точку K. Четырехугольник ABCD таков, что в него можно вписать окружность. Найдите радиус этой окружности, если AB = 3, и LK: KM = 1: 3.
С-18. В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. При этом ∠BAC =
= ∠BDC, а площадь круга, описанного около треугольника BDC, равна
а) Найдите радиус окружности, описанной около треугольника ABC.
б) Зная, что BC = 3, AC = 4, ∠BAD = 90°, найдите площадь четырехугольника ABCD.