Průměr opsané kružnice trojúhelníku. Shrnutí lekce "opsaný kruh". Jak zjistit poloměr kružnice opsané trojúhelníku - obecný vzorec
V této části budeme diskutovat o opsané kružnici kolem (často řečeno „blízko“) trojúhelníku. Nejprve si uveďme definici.
1. Existence a střed kružnice opsané
Zde vyvstává otázka: existuje taková kružnice pro jakýkoli trojúhelník? Ukazuje se, že ano, pro všechny. A navíc nyní zformulujeme větu, která také odpovídá na otázku, kde je střed kružnice opsané.
Vzorce pro zjištění délky úhlopříčky obdélníku
Vzorec na straně obdélníku o průměru a úhlu β. Říká se jí úhlopříčka obdélníku pro jakýkoli segment, který spojuje dva vrcholy protilehlých rohů obdélníku. Vzorec pro úhlopříčku obdélníku ve smyslu dvou stran obdélníku.
Vzorec pro úhlopříčku obdélníku v ploše a na obou stranách. Vzorec pro úhlopříčku obdélníku po obvodu a na obou stranách. Vzorec pro úhlopříčku obdélníku ve smyslu poloměru kružnice opsané. Vzorec pro úhlopříčku obdélníku po obvodu kruhu.
Podívejte, takhle:
Seberme odvahu a dokažme tuto větu. Pokud jste již četli téma „“, přišli jste na to, proč se tři úsečky protínají v jednom bodě, bude to pro vás snazší, ale pokud jste to nečetli, nebojte se: teď to všechno zjistíme ven.
Důkaz provedeme pomocí konceptu lokusu bodů (LPT).
Vzorec pro úhlopříčku obdélníku ve smyslu sinusu úhlu sousedícího s úhlopříčkou a délky strany protilehlé tomuto úhlu. Vzorec pro úhlopříčku obdélníku ve smyslu kosinusu úhlu sousedícího s úhlopříčkou a délky strany sousedící s tímto úhlem. Vzorec pro úhlopříčku obdélníku z hlediska sinusu ostrého úhlu mezi úhlopříčkami a plochou obdélníku.
Vzorce pro určení délky obvodu obdélníku
Obvod obdélníku se nazývá součet délek všech stran obdélníku. Vzorec pro obvod obdélníku ve smyslu dvou stran obdélníku. Vzorec pro obvod obdélníku daný plochou a oběma stranami. Vzorec pro obvod obdélníku podél úhlopříčky a na obou stranách.
No, je například sada kuliček "geometrické místo" kulatých předmětů? Ne, samozřejmě, protože tam jsou kulaté... vodní melouny. Je ale množina lidí, „geometrické místo“, schopna mluvit? Ani ne, protože jsou děti, které neumí mluvit. V životě je obecně obtížné najít příklad skutečného „geometrického místa bodů“. Geometrie je jednodušší. Zde je například to, co potřebujeme:
Vzorec pro obvod obdélníku ve smyslu poloměru kružnice opsané a na obou stranách. Vzorec pro obvod obdélníku daný průměrem kružnice opsané a obou stran. Nazývá se plocha obdélníku v prostoru ohraničeném stranami obdélníku, to znamená uvnitř obvodové oblasti obdélníku.
Vzorce pro určení plochy obdélníku
Vzorec pro oblast obdélníku se dvěma stranami. Vzorec pro oblast obdélníku po obvodu a na obou stranách. Vzorec pro oblast obdélníku podél úhlopříčky a na obou stranách. Vzorec pro oblast obdélníku podél úhlopříčky a sinus ostrého úhlu mezi úhlopříčkami.
Zde je množina prostřední kolmice a vlastnost "" je "být ve stejné vzdálenosti (bodu) od konců segmentu."
Pojďme zkontrolovat? Musíte se tedy ujistit o dvou věcech:
Spojte se s a s. Pak je čára mediánem a výškou v. Takže, - rovnoramenný, - jsme se ujistili, že každý bod ležící na odvěsně je stejně vzdálený od bodů a.
Kruh ohraničený kolem obdélníku
Vzorec pro oblast obdélníku daný poloměrem opsané kružnice a jakékoli strany. Vzorec pro oblast obdélníku v kruhu je kruh kruhu a na obou stranách. Říká se jí kružnice ohraničená kolem obdélníku, kružnice procházející čtyřmi vrcholy obdélníku, jejíž střed je průsečíkem úhlopříček obdélníku.
Vzorce pro zjištění poloměru kružnice opsané obdélníku
Vzorec pro poloměr kruhu ohraničeného obdélníkem přes dvě strany. Vzorec pro poloměr kružnice opsané kolem obdélníku podél obvodu čtverce a obou stran. Vzorec pro poloměr kruhu popsaný kolem obdélníku z hlediska plochy obdélníku a délky jedné z jeho stran.
Vezměte - střed a připojte a. Získal medián. Ale - rovnoramenné podle podmínky, nejen medián, ale i výška, tedy střední kolmice. To znamená, že bod přesně leží na odvěsně.
Všechno! Plně jsme ověřili skutečnost, že kolmice na úsečku je místem bodů stejně vzdálených od konců úsečky.
Vzorec pro poloměr kružnice opsané kolem obdélníku podél úhlopříčky obdélníku. Vzorec pro poloměr kruhu popsaného kolem obdélníku obvodovým průměrem kruhu. Vzorec pro poloměr kruhu popsaného kolem obdélníku ve smyslu sinusu úhlu sousedícího s úhlopříčkou a délky strany protilehlé tomuto úhlu.
Kružnice obklopující daný mnohoúhelník je kružnice opsaná. Většina lidí slyšela termíny obvod a poloměr, ale ohraničený kruh je méně známý termín. Představte si 2D mnohoúhelník s rovnými stranami jako trojúhelník. Představte si kruh kolem trojúhelníku tak, aby se dotýkal všech tří jeho vrcholů; je to omezený okruh. Chcete-li vypočítat svůj poloměr, použijte jednoduchou algebru a kalkulačku.
To je všechno v pořádku, ale zapomněli jsme na opsaný kruh? Vůbec ne, jen jsme si připravili „předmostí pro útok“.
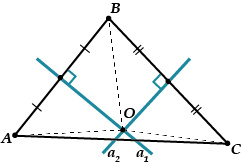
Zvažte trojúhelník. Nakreslíme dvě střední kolmice a řekněme k úsečkám a. Protnou se v nějakém bodě, který pojmenujeme.
Zkontrolujte všechna svá měření a ujistěte se, že kompas říká, že se během kroužení nemění.
- Je nesmírně důležité přesně a přesně měřit.
- Ne všechny polygony mohou mít ohraničený kruh.
Plocha kruhu vepsaného do šestiúhelníku se tedy rovná. Nyní se obracíme na napsaný čtverec. Vzhledem k tomu, že úhlopříčka čtverce je rovna straně odmocnin, máme. Potom poloměr kruhu vepsaného do čtverce bude mít polovinu míry strany. Uvidíte tedy, že poloměr kruhu vepsaného do trojúhelníku je poloviční než poloměr kruhu opsaného trojúhelníku, protože obvod kruhu je popsán rozděleným prostředím na dvě části úměrné 1 a pak poloměr vepsaného kruhu bude.
A teď pozor!
Bod leží na odvěsně;
bod leží na odvěsně.
A to znamená a.
Z toho vyplývá několik věcí:
Za prvé, bod musí ležet na třetí kolmici k úsečce.
Měření a aproximace kruhu
Plocha vepsaného kruhu tedy bude. A problém je dokázat, že součet těchto oblastí se rovná ploše vnitřního kruhu. Udělejme tedy součet ploch korun. Jedná se o součet ploch korun. Můžete vidět, že máme 3 kruhy paprsků. Tento článek navrhuje hypotézu, záminku pro zvážení některých bodů matematiky tohoto období v Mezopotámii.
Vytvořením kruhu mezi dvěma šestiúhelníky, jehož obvod lze snadno vypočítat, a následným zdvojnásobením počtu stran, získá rám s mnohoúhelníky s 96 stranami. Pravděpodobně je jednodušší hodnotit výkon zadáním číselných hodnot.
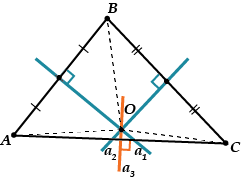
To znamená, že bodem musí procházet i odvěsna a všechny tři odvěsny se protínají v jednom bodě.
Za druhé: nakreslíme-li kružnici se středem v bodě a poloměrem, pak bude i tato kružnice procházet bodem a bodem, to znamená, že to bude kružnice opsaná. To znamená, že již existuje, že průsečík tří kolmých os je středem kružnice opsané pro jakýkoli trojúhelník.
Vidíme zde zajímavost a efektivitu pozorovacích metod: na jedné straně poskytují přiblížení a na druhé straně umožňují kontrolovat dokonalou chybu. Pokud vím, Archimedes je první, kdo výslovně zdůvodnil své výsledky týkající se kruhu, a uvádí krok za krokem řadu argumentů vysvětlujících, proč je to, co tvrdí, pravda. Není ale první, koho kruh a jeho míra zajímá. Máme velmi starodávné důkazy, jeden v Egyptě a některé další v Mezopotámii, jdoucí tímto směrem.
A existují některé „babylonské“ hliněné tabulky pocházející ze stejného období a podél obvodu nebo oblasti disku. To je předmětem tohoto článku. Procházka může začít, ale před odjezdem do Babylonu 17. nebo 18. století před naším letopočtem. Byla nalezena babylonská hliněná tabulka, která udává poměr obvodu šestiúhelníku k obvodu jeho opsané kružnice.
A poslední věc: o jedinečnosti. Je jasné (téměř), že bod lze získat jedinečným způsobem, a proto je jedinečný i kruh. No, "skoro" - to necháme na vás. Zde jsme dokázali větu. Můžete křičet "Hurá!".
A pokud je problém otázka „najít poloměr kružnice opsané“? Nebo naopak, rádius je daný, ale potřebujete najít něco jiného? Existuje vzorec vztahující poloměr kružnice opsané k ostatním prvkům trojúhelníku?
A často se přidávají v té či oné podobě. To byl druhý problém, který mi dal problém: mohli Babyloňané skutečně experimentálně zjistit tuto hodnotu? V současné době je zkušenost snadno použitelná, s švadlenou a předměty každodenní potřeby různých průměrů: pánev, kastrol, plechové dózy. Změří se obvod a průměr a provede se dělení. Rozdíly byly na třetím desetinném místě. Samozřejmě neexistují tak přesné průmyslové předměty, ani švadleny metry odstupňované po milimetrech.
Pro měření je tenčí: lano, kožený řemínek, může se pod napětím natahovat a snadno stahovat. Na druhou stranu sušená papyrusová kůra se neprodlužuje. Bohužel jsem ho neměl. Je zřejmé, že nejsou odstupňované, ale to není vážné: zajímá nás poměr dvou délek: od obvodu a průměru, a ne od délek samotných. Je snadné předmět s ratanem obejít a rozřezat. Je zvláštní, že je méně snadné přesně řezat ratanovou nit tak, aby odpovídala průměru. Horní okraj keramiky je skutečně často zaoblený.
Velmi často při řešení geometrických problémů musíte provádět akce s pomocnými postavami. Najděte například poloměr vepsané nebo opsané kružnice atd. Tento článek vám ukáže, jak zjistit poloměr kružnice opsané trojúhelníku. Nebo, jinými slovy, poloměr kružnice, ve které je trojúhelník vepsán.
Proto je nutné ratan po obvodu zafixovat a následně uříznout druhý ratanový nůž, odpovídající vnitřnímu průměru prvního. Zbývá vypočítat poměr dvou délek, aniž bychom je znali přesné hodnoty, což lze provést návratem k samotnému původu dělení. 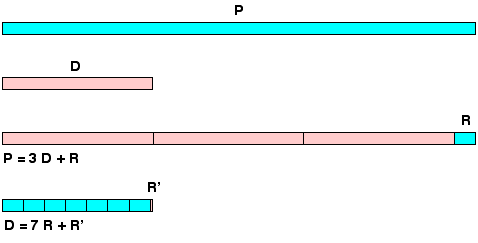
Můj nejlepší výkon byl 6x, 8x, tedy 6x, s nádherným odpočinkem. Tyto experimenty mě však přesvědčily, že Babyloňané nezískali experimentální hodnotu, alespoň ne z této cesty. V tomto případě ale vyvstávají dvě otázky.
Jak zjistit poloměr kružnice opsané trojúhelníku - obecný vzorec
Obecný vzorec je následující: R = abc/4√p(p - a)(p - b)(p - c), kde R je poloměr kružnice opsané, p je obvod trojúhelníku dělený 2 (půlobvod). a, b, c jsou strany trojúhelníku.
Najděte poloměr kružnice opsané trojúhelníku, jestliže a = 3, b = 6, c = 7.
Otázka 1: Pokud není experimentální, je teoretická, geometrická. 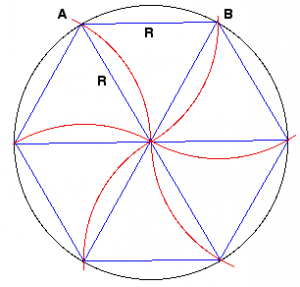
Obvod P kruhu je tedy větší než obvod šestiúhelníku a poměr mezi nimi je stejný. Je pro nás zcela přirozené odhadovat obvod kruhu, neznámý ve vztahu k tomu, co je známo samotnému šestiúhelníku.
Později uvidíme, co si o tom myslet. Hypotéza 1: Babyloňané znali Pythagorovu větu před tisíci lety. Hypotéza 2: Věděli, že našli obdélníky celočíselných stran. Možná ne všechny, ale alespoň ty, jejichž přepona a jedna ze stran jsou celá celá čísla.
Na základě výše uvedeného vzorce tedy vypočítáme poloobvod:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Nahraďte hodnoty ve vzorci a získejte:
R = 3 x 6 x 7/4√8 (8 - 3) (8 - 6) (8 - 7) = 126/4√ (8 x 5 x 2 x 1) = 126/4√80 = 126/16 √5.
Odpověď: R = 126/16√5
Jak zjistit poloměr kružnice opsané rovnostrannému trojúhelníku
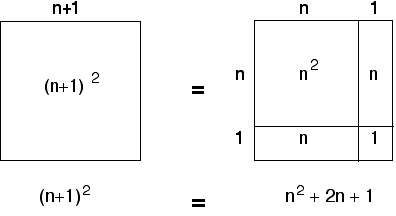
Pro nalezení poloměru kružnice opsané rovnostrannému trojúhelníku existuje poměrně jednoduchý vzorec: R = a/√3, kde a je velikost jeho strany.
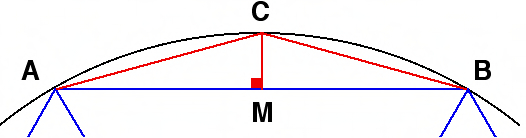
Samozřejmě neexistuje žádný důkaz, že to Babyloňané udělali. To dokáže pouze objev nové hliněné tabulky. Navíc je tato myšlenka založena na hypotéze 1 a věděli Babyloňané skutečně, jak takové trojúhelníky najít? 
Posledních 15 řádků je rozděleno do 4 sloupců, z nichž první dva řádky definují obsah. Sloupec 4 obsahuje znaménko následované čísly od 1 do.
Příklad: Strana rovnostranného trojúhelníku je 5. Najděte poloměr kružnice opsané.
Protože jsou všechny strany rovnostranného trojúhelníku stejné, k vyřešení problému stačí zadat jeho hodnotu do vzorce. Dostaneme: R = 5/√3.
Odpověď: R = 5/√3.
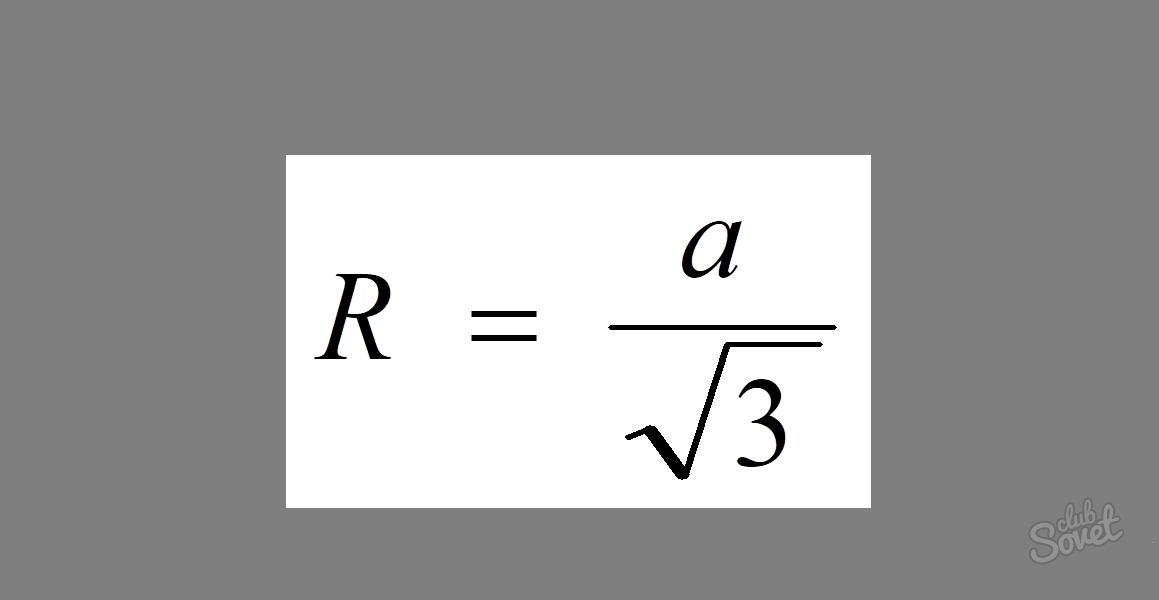
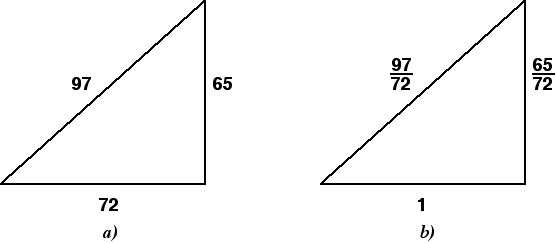
Jak zjistit poloměr kružnice opsané pravoúhlému trojúhelníku
Vzorec vypadá takto: R = 1/2 × √(a² + b²) = c/2, kde aab jsou nohy a c je přepona. Sečteme-li druhé mocniny nohou v pravoúhlém trojúhelníku, dostaneme druhou mocninu přepony. Jak je vidět ze vzorce, tento výraz je pod kořenem. Výpočtem odmocniny druhé mocniny přepony dostaneme samotnou délku. Vynásobením výsledného výrazu 1/2 se nakonec dostaneme k výrazu 1/2 × c = c/2.
Sloupce 1, 2 a 3 odkazují na pravoúhlé trojúhelníky. Sloupce 2 a 3 uvádějí nejmenší stranu a přeponu každého trojúhelníku. Sloupec 1 udává druhou mocninu poměru na obou stranách pravého rohu. Například linie 5 začíná v sexuálním systému.
To je příliš přesné, než aby to byla pravda, ale můžete zkontrolovat, zda je to stejné pro ostatní řetězce. Existuje polemika o metodách, které mohli Babyloňané použít k sestavení této tabulky. V opisu písaře jsou také chyby a malé záhady, jako je řádek 11, který dává 45 a 1 15 jako strany, tedy v desítkovém číslování: 45, a oba jsou násobky 15, a tento trojúhelník není nic jiného než trojúhelník stran . Proč to není uvedeno v této podobě, mnohem jednodušší? A jaká by mohla být výhoda dát čtverec svahu spíše než svah samotný?
Příklad: Vypočítejte poloměr opsané kružnice, pokud jsou ramena trojúhelníku 3 a 4. Dosaďte hodnoty do vzorce. Dostaneme: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2,5.
V tomto výrazu je 5 délka přepony.
Odpověď: R = 2,5.
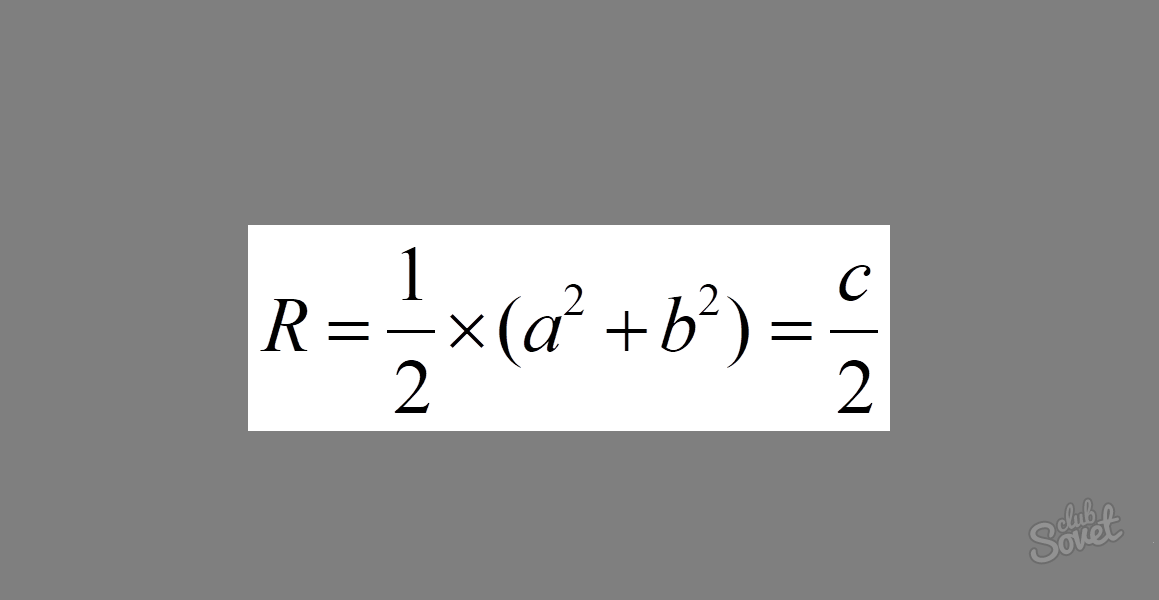
Jak zjistit poloměr kružnice opsané rovnoramennému trojúhelníku
Vzorec vypadá takto: R = a² / √ (4a² - b²), kde a je délka stehna trojúhelníku a b je délka základny.
Příklad: Vypočítejte poloměr kruhu, je-li jeho bok = 7 a jeho základna = 8.
Řešení: Tyto hodnoty dosadíme do vzorce a získáme: R \u003d 7² / √ (4 × 7² - 8²).
R = 49/√(196-64) = 49/√132. Odpověď lze napsat přímo takto.
Odpověď: R = 49/√132
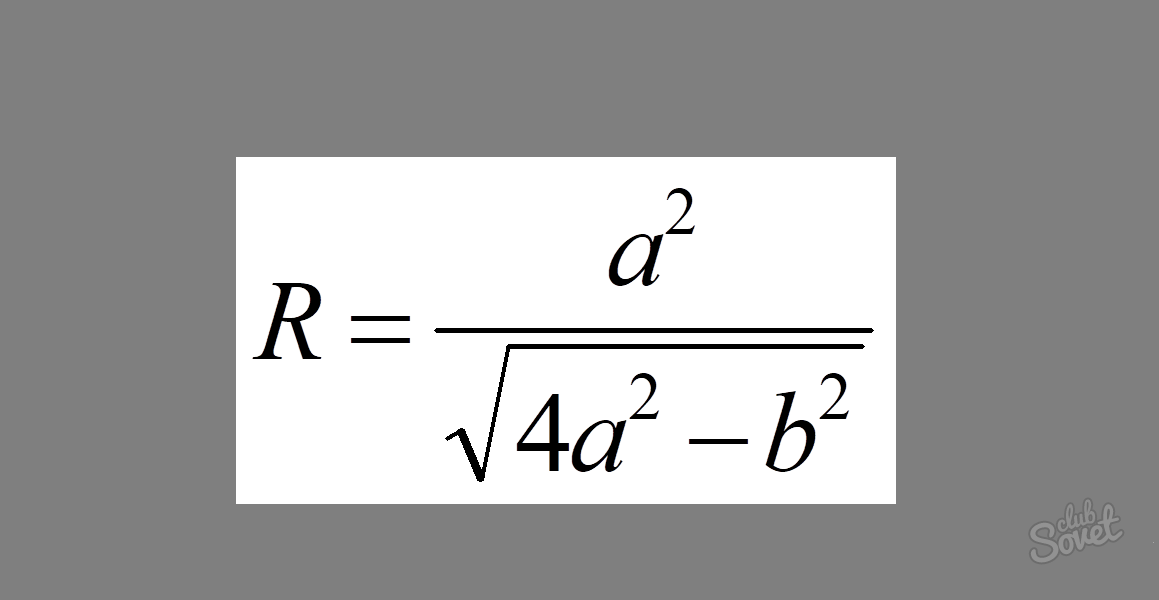
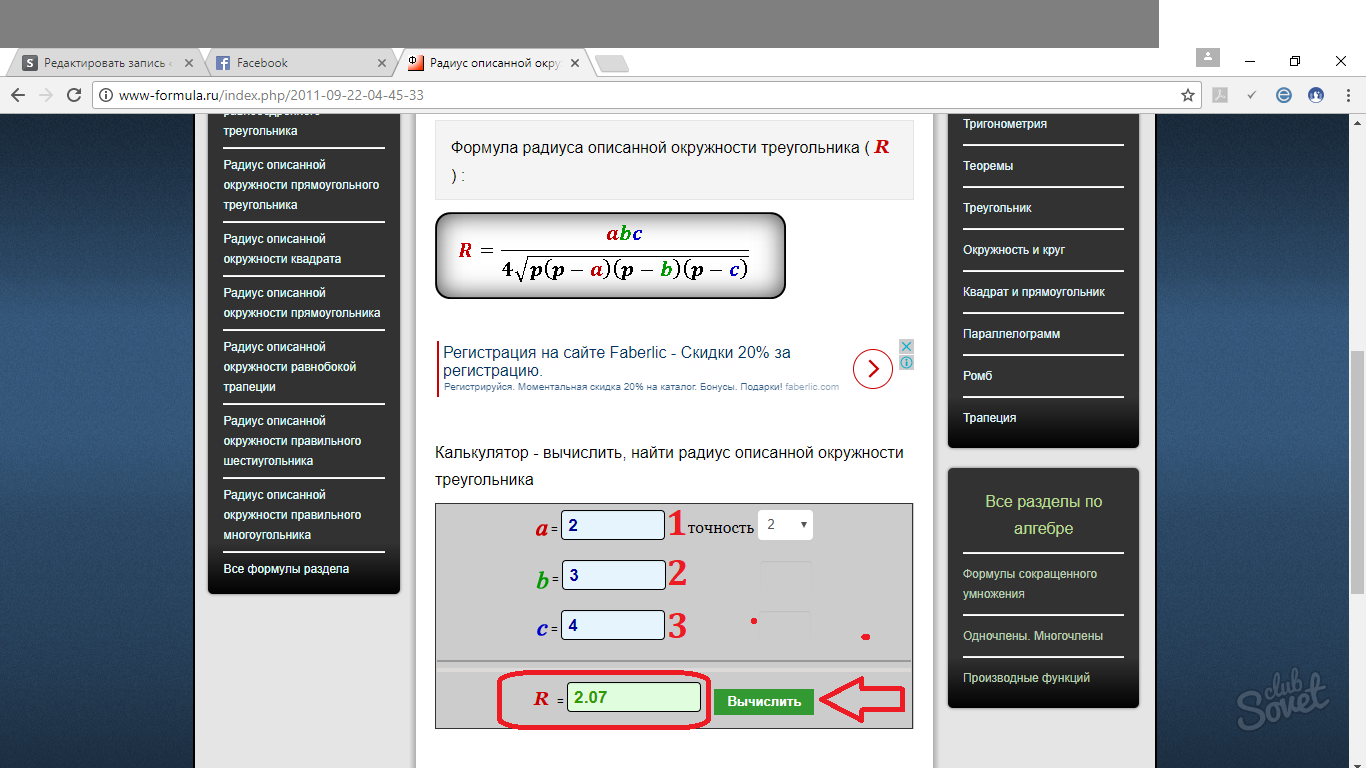
Online zdroje pro výpočet poloměru kruhu
Ve všech těchto vzorcích je velmi snadné se splést. Proto v případě potřeby můžete použít online kalkulačky, který vám pomůže při řešení problémů s hledáním poloměru. Princip fungování takových mini-programů je velmi jednoduchý. Dosaďte hodnotu strany do příslušného pole a získejte hotovou odpověď. Můžete si vybrat několik možností zaokrouhlení odpovědi: na desetinná místa, setiny, tisíciny atd.