How to calculate the circumference of a pipe by diameter. Methods for measuring circumference. Checking the diameter of pipes and other parameters under production conditions: external, internal indicators.
And how is it different from a circle? Take a red pen or pencil and draw a regular circle on a piece of paper. Fill in the entire middle of the resulting figure with blue; the outline indicating the boundaries of the figure is a circle. But the blue content inside it is the circle.
The dimensions of a circle and a circle are determined by the diameter. On the red line indicating the circle, mark two points so that they are mirror images of each other. Connect them with a line. The segment will definitely pass through the point in the center of the circle. This segment connecting opposite parts of a circle is called a diameter in geometry.
Forms of work: - individual work, - work in groups. Introduction to the subject, purpose of the course. For today's activities you would bring three wheels with a diameter of 6 cm, 8 cm, 10 cm and a rope about 50 cm long, a ruler and a calculator. Do you think these items will be needed today? We will calculate the circumference of the wheels using twine and a ruler.
Yes, today we will calculate the circumference of wheels using a string, but we will not always do this today. As you remember, the patterns of arbitrary polygons are related to the lengths of the corresponding sides. The perimeter of a square contains the lengths of four sides of equal length, the circumference of a rectangle contains two lengths and two widths, the circumference of a right triangle contains the lengths of its three sides, and what relationship can be shown in a circle or circle? Reynolds number Students: The circumference of a circle depends on its radius.
A segment that does not extend through the center of the circle, but joins it at opposite ends, is called a chord. Consequently, the chord passing through the center point of the circle is its diameter.
 Diameter is indicated Latin letter D. You can find the diameter of a circle using values such as area, length and radius of the circle.
Diameter is indicated Latin letter D. You can find the diameter of a circle using values such as area, length and radius of the circle.
Yes, today we will look at the relationship between the circumference of a circle and the diameter of the circle and the length of the circle. Exercise 1Select the length of the diameter of the object. Measure its circumference, i.e. the length of the circle using thread, thread or tailor. Divide the length of the circle by the length of the diameter. Repeat these measurements and counts for items.
Diameter of an object's circumference The ratio of the circumference of a circle to the length of its diameter. Calculations are made using calculators and results are rounded to 0. Several sample measurements are written on the board. Students note that the number of diameters in the circumference of a circle is slightly greater than.
The distance from the central point to the point plotted on the circle is called the radius and is denoted by the letter R. Knowing the value of the radius helps to calculate the diameter of the circle in one simple step:
For example, the radius is 7 cm. We multiply 7 cm by 2 and get a value equal to 14 cm. Answer: D of the given figure is 14 cm.

For years, scientists have tried to determine the exact size of pi; unfortunately, it is an irrational number and cannot be calculated accurately. In our calculations we will most often use a record or approximate number. Exercise 3 Create a template for the length of the circle. Based on the measurements taken, we know that.
Instead of the length of the diameter, we can insert the length of the two rays and we get the figure for the length of the circle. Divide the class into 4 groups and solve problems. Each group of problems 1, 2 and 6 receives one example to solve. Solution. During class, the teacher records the points collected by each group in a table. At the end of the lesson, the collected points are counted. The sum of the points in a group determines the location of the group. Meeting and systematization of the message. Review of basic messages about circle and circle: difference between circle and circle, radius, diameter.
Sometimes you have to determine the diameter of a circle only by its length. Here it is necessary to apply a special formula to help determine Formula L = 2 Pi * R, where 2 is a constant value (constant), and Pi = 3.14. And since it is known that R = D * 2, the formula can be presented in another way
This expression is also applicable as a formula for the diameter of a circle. Substituting the quantities known in the problem, we solve the equation with one unknown. Let's say the length is 7 m. Therefore:
Appendix: Work assignment for staff. How long is the circumference of a 10cm circle from a 10cm circle? Good practice with angles in a circle is necessary to work on the following topics: simple tangents to circles, tangents to circles and quadrilaterals in a circle, quickly and smoothly. If you can master the basic methods of corner angles based on the same arc, and the relationship between the average angles and those that were printed to make them almost mechanically, without going back to the content of the statements, it will be much easier to understand problem solving for further problems .
Answer: the diameter is 21.98 meters.
If the area is known, then the diameter of the circle can also be determined. The formula that is used in in this case, looks like that:
D = 2 * (S / Pi) * (1 / 2)
S - in this case Let's say in the problem it is equal to 30 square meters. m. We get:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
When the value indicated in the problem is equal to the volume (V) of the ball, the following formula for finding the diameter is used: D = (6 V / Pi) * 1 / 3.
Therefore, in the following examples we will show how to use assertions in this chapter and in what situations you might need them. The examples are very easy to convey to those seeing this for the first time and more complex problems, with solutions presented as sequences of further observations - these can be used to test your skills, solve them yourself, as a hint.
Let's start with a fact that you need to not only remember, but also be able to apply even in the middle of the night: a triangle, two vertices of which lie on a circle, and the third is the center of this circle, isosceles. Only two of its sides, leading from the center of the circles to the points on its edge, are radii, so they are equal.
Sometimes you have to find the diameter of a circle inscribed in a triangle. To do this, use the formula to find the radius of the represented circle:
R = S/p (S is the area of the given triangle, and p is the perimeter divided by 2).
We double the result obtained, taking into account that D = 2 * R.
Often you have to find the diameter of a circle in everyday life. For example, when determining what is equivalent to its diameter. To do this, you need to wrap the finger of the potential owner of the ring with thread. Mark the points of contact of the two ends. Measure the length from point to point with a ruler. We multiply the resulting value by 3.14, following the formula for determining the diameter with a known length. So, the statement that knowledge of geometry and algebra is not useful in life is not always true. And this is a serious reason for taking school subjects more responsibly.
Another, slightly more difficult problem that is well seen as an opportunity to try to solve yourself with the help of guidance. But beyond this triangle we know too little to count. After reviewing the most basic fact of this chapter, let's move on to the equally important ones - mean and inscribed angles and the relationships between them. We must remember two basic tools.
A central angle based on some arc is twice the angle written on the same arc. Two angles inscribed along the same arc have the same measure. Sometimes a slightly more powerful version of the second tool is useful. Two angles inscribed on arcs of the same length have the same measure.
§ 34. Circumference
Preliminary exercise
Tie a thread around a round object (a glass, a pan, a sieve) around the circumference and, stretching the thread, measure it. Then determine how many times the circumference of this object is greater than its diameter.
In practice, it is often necessary to determine the circumference. To prepare, for example, an iron strip for a wheel tire, the blacksmith needs to know in advance the length of this strip, i.e., the circumference of the wheel. The easiest way in this case is to cover the wheel rim with thread and then, pulling it out, measure its length. However, it is not always convenient to do this, and often this method is not applicable at all: for example, it is impossible to find the length of a circle drawn on paper using this method.
To make these properties better remembered, let's move on to the exercises. Examples 3 and 4 deal with average and typed angles, Example 5 uses the properties of angles written from the same arc, while Example 6 is the exercise at the end of this topic.
Theorem 2, which we will discuss further, will help us interpret this. The best one we know of. But from the content of the problem we know that the measurements of these angles are up to 90 degrees. Finally, an example with some tips for self-study. Is it possible to express other angles using α?
Which angles can we describe more accurately now? Therefore he has twice as much, i.e. \\. Can you explain how this comes from ownership? We've used it in earlier examples, but now we'll take a closer look at how to use it in a more complex and interesting case.
Another way to determine the circumference is to measure only the diameter and use it to find out the circumference using the following property circles:
Length of the entire circumference and larger diam eter is approximately 3.14 r a z a.
If, for example, the length of the diameter is 75 cm, then the circumference is 75 ? 3.14? 240 cm. This rule is true for any circle, no matter how small or how large its dimensions.
We would like to see a circle in the drawing to apply the angular properties above - proof that a triangle is equilateral can be done by calculating that all its angles are 60 degrees. Besides, we already said that property will be useful here.
Now we can look at the angles in this circle. How can we find its measure? It turns out that this is actually the end of the solution. In solving this problem, we proved an important property that will be useful several times when working on other problems. The center of a circle circumscribed on a right triangle is the hypotenuse of that triangle.
By checking the correctness of this ratio by direct measurement (diameter - with a scale ruler, circumference - with a thread or tape), we get numbers only more or less close to 3.14. The discrepancy between the results is explained by measurement errors: it is very difficult to measure the diameter and circumference absolutely accurately, and therefore one cannot vouch for the strict accuracy of their ratio obtained in this way. But in mathematics there are other ways to find this ratio, which we cannot present here, but which give the ratio of the circumference to the diameter with an accuracy more than sufficient for practical purposes.
It's good to know what to do with this information - for example, how to translate it into the language of angles into a circle, which we have here. The best thing to remember is that the central angle is this fraction full angle, and the fraction of a circle is the length of the arc on which it is based. Let's look at how to apply this rule to problems - one solution that we describe exactly, another that is a little more complicated, we give in the form of a series of instructions, so they relate well to the exercise.
According to the above rule, we first interpret the arc length information. To use it, let's look at drawing the mean and inscribed angles based on these arcs. At this stage, both approaches should be combined into one solution.
The number showing how many times the circle is longer than the diameter (i.e., expressing the ratio of the circumference to the diameter), it was agreed for the sake of brevity to be denoted by a Greek letter (pronounced: “pi”). Approximately?= 3.14; more exact values of this value are expressed a large number digits after the decimal point. In practice, in most cases it is enough to use the value given now (= 3.14), which therefore must be firmly remembered. So,
And after substituting the calculated values \\. Let's now think about how to come to a decision. How to determine the length of a certain arc? Since we know the length of the circle, we can determine the length of this arc. Wheel? The set of all points on a plane whose distance from a fixed point is less than or equal to a given distance.
Circle? - the set of all points on the plane whose distance from a fixed point is equal to a given distance. Simply put, a circle is the edge of a circle. 
The following terms are associated with the circle. A chord is a segment connecting two points lying on a circle, a diameter is a chord passing through the center of the circle, a tangent is a straight line that has exactly one common point with the circle. 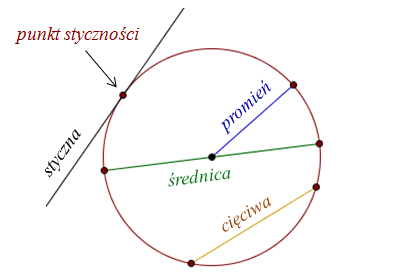
Radius, chord, diameter, tangent and tangent point.
The ratio of the length of the entire circumference to the dimension is equal, i.e. . 3.14 and l and 31/7.
It follows that if the diameter of the circle d, then its length C = ? ? d, or?d
(pronounced "pi deh")
If the radius of the circle R, then its length
WITH= 2R?= 2?R(“two pi er”).
Using these formulas, calculate the circumference of a circle by its diameter or radius.
All points marked in this figure are points belonging to the circle. Note! The center of the circle does not belong to the circle! A circle is a collection of only those points that are located on the edge of the circle. The concepts of chord, diameter, and tangentiality also apply to a circle because a circle is the edge of a circle. Of course, the center of the wheel belongs to the wheel.
Calculate the circumference and circumference of a circle whose diameter is \\. The diameter of the circle consists of two rays. In a circle we can identify two very important angles. The central angle is the angle whose tip lies on the center of the circle and the arms are the rays, the angle is the angle where the vertex lies on the circle and the arms are the chord. 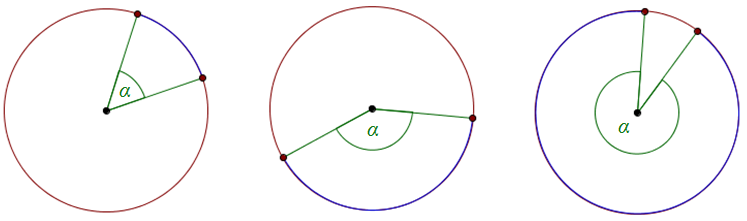
Blue indicates the arches on which the inscriptions and the above central angles are typed.
On the contrary, knowing the circumference of a circle, you can use the same formulas to calculate its diameter or radius:
Let, for example, we want to determine the diameter of a tree (i.e., the diameter of its cross-section). Measuring the circumference of the tree with a tape, we get, say, 86 cm: this is the circumference. Its diameter, i.e. diameter, is 86: 3.14 = 27 cm.
Repeat questions
If central angles and lettering are based on the same arc, the measure central angle twice as high. 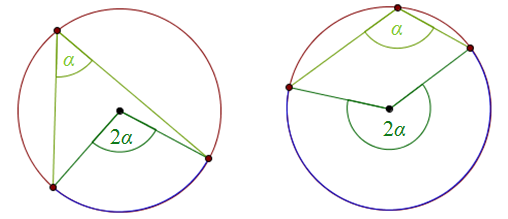
Examples of mean and inscribed angles based on the same arc. You can find more material on center and inscribed angles on this page. The next concepts of circle and circle are arc of circle, segment of circle and segment of circle.
The first will consider the geometric properties of the organic derivation of the figures involved: circle, square and square dialed circle. Almost certainly the first measurements of π were found from measurements. For example, take a string and measure the cylinder's circumference and diameter and make a ratio of them, since it was about the same number of diameters that the cylinder would have. Apparently, here we are not talking about geometry, but about geometric calculation. And the Jews in the same geographic area considered it equal, as evidenced in the Bible, as the measure of a large 10 cm brass basin and a 30 cm circumference.
How to determine the circumference of a circle by measurement? What is the calculation based on to find the circumference of a circle? – What is the ratio of the circumference of a circle to its diameter? What did you agree to represent with the letter? – What’s the same? – How to determine the circumference of a circle by its diameter? By radius? – How to determine the diameter from the circumference? Radius along the circumference? How to express these relationships in formulas?
And the Chinese until the 3rd century, i.e. AD everyone considered it equal, apparently, there was probably an empirical dependence, even when there are two decimal brain and geometric calculations. He also gave one that is valid for a sphere: "Spheres are in the ratio of cubes of diameters." The problem is whether he went further and explored all the consequences of this approach - the "organic" problem area of the circle and therefore the volume of the sphere. Recommend the author to move from the same report in the case of a sphere and citation: This report 3. 14 over 4 is supported as the ratio of the area of the square of a circle and the area between the sphere and the cube respectively.
Applications
39. A meter is 40,000,000th the circumference of the globe. Find the radius of the Earth.
Solution. Let's find the radius dividing the circle by 2, i.e. by 6.28.
40,000,000: 6.28 = 6,370,000 meters.
40. The driving wheel of a steam locomotive makes 4 revolutions per second. The diameter of the wheel is 1.3 m. Determine the hourly speed of the locomotive.
Solution: For one revolution of the wheel, the locomotive moves 3.14 ? 1.3 m. Therefore second speed = 4 ? 3,14 ? 1.3, and hourly
4 ? 3,14 ? 1,3 ? 3,600 = 59,000 m = 59 km.
41. A passenger locomotive passes at 60 o'clock km. Drive wheel diameter 2.1 m. How many whole revolutions does the wheel make per second?
Solution: For one revolution of the wheel, the locomotive moves 3.14 ? 2.1 = 6.6 m. Since per second it moves by
60,000/3600 = 17 meters, then the required number of revolutions is 17: 6.6, i.e. about 21/2.
42. Leningrad lies 25° east of the Greenwich meridian. Christiania - on the same parallel circle 11° east of the Greenwich meridian. The radius of the parallel circle on which these cities are located is 3200 km. Determine the mutual distance of these cities along the arc of a parallel circle.
Solution. The distance between the named cities in degrees is 250° – 11° – 140°. The length of a parallel circle is
2 ? 3,14 ? 3200 = 20,000 km. The length of 1° of this circle = 55 km. The required distance is 770 km.



















