Among the variety of geometric shapes, a quadrilateral such as a rhombus stands out noticeably. Even its name itself is not typical for the designation of quadrangles. And although in geometry it is found much less frequently than such simple figures as a circle, triangle, square or rectangle, it also cannot be ignored.

Below are the definition, properties and characteristics of rhombuses.

Definition

A rhombus is a parallelogram with equal sides. A rhombus is called a square if all its angles are right angles. The most striking example of a rhombus is the image of the suit of diamonds on playing card. In addition, the rhombus was often depicted on various coats of arms. An example of a rhombus in Everyday life could serve as a basketball court.

Properties

1. The opposite sides of a rhombus lie on parallel lines and have the same length.
2. The intersection of the diagonals of a rhombus occurs at an angle of 90° at one point, which is their midpoint.
3. The diagonals of a rhombus bisect the angle from whose vertex they emerged.
4. Based on the properties of a parallelogram, we can derive the sum of the squares of the diagonals. According to the formula, it is equal to the side raised to a quadratic power and multiplied by four.

Signs

We must clearly understand that any rhombus is a parallelogram, but at the same time, not every parallelogram has all the indicators of a rhombus. To distinguish these two geometric shapes, you need to know the characteristics of a rhombus. Listed below are characteristic features given geometric figure:

1. Any two sides with a common vertex are equal.
2. The diagonals intersect at an angle of 90°C.
3. At least one diagonal divides the angles from whose vertex points it emerges in half.

Area formulas

Basic formula:

• S = (AC*BD)/2

Based on the properties of a parallelogram:

• S = (AB*H AB)

Based on the size of the angle between two adjacent sides of the rhombus:

• S = AB2*sinα

If we know the length of the radius of a circle inscribed in a rhombus:

• S = 4r 2 /(sinα), where:
  • S - area;
  • AB, AC, BD - designation of sides;
  • H - height;
  • r - radius of the circle;
  • sinα - sine alpha.

Perimeter

To calculate the perimeter of a rhombus, you just need to multiply the length of any of its sides by four.

Construction of the drawing

Some people have difficulty constructing a diamond pattern. Even if you have already figured out what a rhombus is, it is not always clear how to construct its drawing accurately and in compliance with the necessary proportions.

There are two ways to construct a diamond pattern:

1. First construct one diagonal, then a second diagonal perpendicular to it, and then connect the ends of adjacent segments in pairs parallel sides rhombus
2. First set aside one side of the rhombus, then construct a segment equal in length parallel to it, and connect the ends of these segments also in pairs in parallel.

Be careful when constructing - if in the drawing you make the length of all sides of the rhombus the same, you will not get a rhombus, but a square.

Lesson Objectives

Continue to introduce students to such a geometric figure as a rhombus;
Consolidate knowledge about concepts such as rhombus and square, and also learn to determine their difference;
To refresh students' knowledge about the properties and characteristics of a rhombus;
Continue to improve students' knowledge of geometric shapes through problem solving.
Arouse interest in geometry lessons.

Lesson Objectives

Repeat, generalize and consolidate the acquired knowledge about such a geometric figure as a rhombus;
Continue to develop skills in constructing geometric figures;
Improve rhombus construction skills using drawing tools;
Continue to consolidate students’ knowledge using practical assignments;
Continue to develop attention, perseverance and desire for the cognitive process.

Lesson Plan

1. Disclosure of the main topic of the lesson, definition of the geometric figure “Rhombus”.
2. Familiarization with the properties and characteristics of a rhombus.
3. Theorems and their proof.
4. How to draw a rhombus. Ways to depict a rhombus.
5. How to find the area of ​​a rhombus?
6. Repetition of the material covered.
7. Interesting facts.
8. Homework.

Definition of a rhombus as a geometric figure

A rhombus is a parallelogram in which all sides are equal. If a rhombus has right angles, then it is called a square.

The term "Rhombus" itself translated from Greek language, means "tambourine". Of course, in our understanding, the tambourine, as a musical instrument, has a round shape. But now tambourines are made round, but in ancient times it had a square or diamond shape.

Let's look at the basic definitions of a rhombus and try to understand what this geometric figure is.

A rhombus is an equilateral parallelogram that has equal sides but unequal angles.

Unlike a square, a rhombus is an equilateral oblique angle.

As always, we receive many definitions of this or that geometric figure, but this does not mean that every student should sit down and “memorize” these very definitions. The difference in definitions is how broadly they describe our geometric figure. The most important thing is to understand what the definition is talking about and the ability to imagine the figure. If you adhere to these two rules, then you yourself will be able to write or add a couple of definitions.

Properties of a rhombus

2. Its second property is that all diagonals of a rhombus intersect at right angles. At the point of intersection, the diagonals of the rhombus are divided in half.

3. The bisectors of the angles of a rhombus are its diagonals.

4. To find the sum of the squares of the diagonals of a rhombus, you need to multiply the square of its side by four.

5. Opposite sides of a rhombus are equal;

6. The sum of the angles of a rhombus that are adjacent to one side is 180 degrees.

Signs of a diamond

A parallelogram is a rhombus if it meets the following conditions:

1. Firstly, all its sides are equal to each other;
2. Secondly, the diagonals of a rhombus intersect at right angles.
3. Thirdly, if the diagonals of its angles are bisectors.
4. Fourthly, if its two adjacent sides are equal to each other.
5. Fifthly, if at least one of the diagonals is a bisector of a parallelogram.

Theorems and their proof

Now let's take a closer look at the properties and characteristics of a rhombus, proving the theorems:

Theorem 1

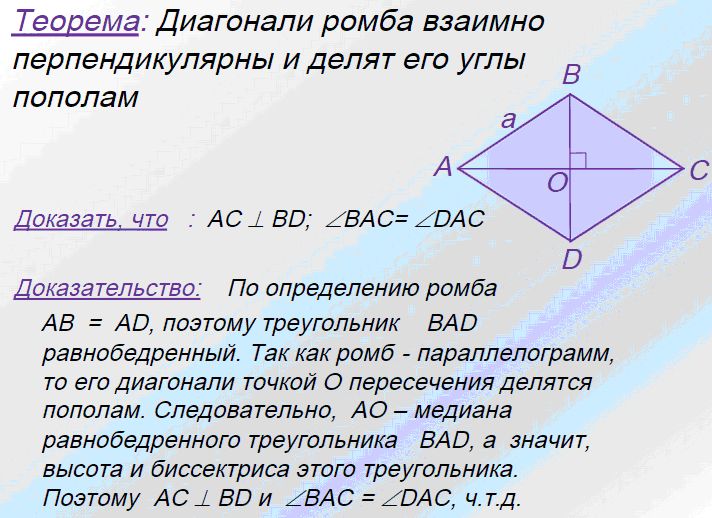
Theorem 2

It follows that:

1. A rhombus has two axes of symmetry - diagonals AC and BD.
2. Its diagonals are mutually perpendicular.
3. And also are the bisectors of its angles.

Area of ​​a rhombus

The area of ​​a rhombus is equal to half the product of its diagonals. But since a rhombus is essentially a parallelogram, its area can be found by multiplying its sides by its height.

Formulas for the area of ​​a rhombus:

Where: a – is the side of the rhombus
D – its large diagonal is indicated
d – designated smaller diagonal
α is an acute angle
β – is an obtuse angle

The area of ​​any geometric figure is the part of the surface that is limited by the closed contour of this figure. And the area of ​​a rhombus is expressed by the number of square units it contains.

How to draw a rhombus

To draw a rhombus, we will use the properties of the diagonals of a rhombus. We already know that the diagonals of our geometric figure are mutually perpendicular and bisected at the point of intersection. Therefore, the easiest way to start constructing a rhombus is to construct its diagonals.

First way

And so, first of all, we select a point from which we lay out segments of the same length to the left and right, and identical segments of a different length up and down.

Now all we have to do is connect the ends of these segments, and as a result we will get a rhombus.

Second way

A rhombus can also be drawn without using diagonals. In this case, you only need to determine the ends of the diagonals and then connect the points with segments.

Third way

And finally, the third method, drawing a rhombus can be done using a ruler. Since you and I know that a rhombus has equal sides, we first need to draw its lower part. Then you need to set aside an equal segment from it. And since the third side is parallel to the first, connecting the ends of the first and third segments, we get a rhombus.

Repetition

You have already become acquainted with such a geometric figure as a rhombus and understand that the square is its special case.

1. Therefore, let's remember the definition, what is a square? Give your own definition of a square.
2. What properties does a square have? Name them.
3. What is the difference between a rhombus and a square, if the square is its special case?
4. What figure is called a quadrilateral, and does a rhombus belong to this geometric figure?
5. What types of quadrilaterals have you already studied? Name them.
6. What differences exist between them?

It's interesting to know

Did you know that if we take a rectangle and connect the midpoints of its sides with segments, we will end up with a rhombus.

But if, on the contrary, we take a rhombus and try to connect its midpoints with segments, then we will get a geometric figure like a rectangle.

If you take a parallelogram with equal heights, then such a parallelogram is a rhombus.

Did you know that the name of the card suit of tambourines, which has a rhombic shape, appeared back in the days when the tambourine was far from round in shape, but in the form of a rhombus or square.

For the first time the word "rhombus" was used in his vocabulary by Gerron and Pope of Alexandria.

Homework

1. Do you think a rhombus is a parallelogram that has at least one right angle?
2. Is it true that every parallelogram is a rhombus?
3. If the diagonals of a parallelogram are 5 cm and 7 cm, can this parallelogram be a rhombus?
4. If the diagonals of a parallelogram are equal, then can it be a rhombus?
5. What is the special property of a rhombus that its diagonals have, in addition to the fact that they are divided in half by the point of intersection?
6. Think about where a geometric figure such as a rhombus is used in everyday life?

Subjects > Mathematics > Mathematics 8th grade

A rhombus is a quadrilateral whose sides are equal and pairwise parallel. Unlike a square, which has right angles, a rhombus has two acute and two obtuse angles, lying on opposite sides. But the diagonals intersect at right angles and are at the same time bisectors. The intersection point of the diagonals divides them into equal parts.

There are many formulas for finding the diagonals of a rhombus; you just need to know the initial data and choose the appropriate one.

How to find the diagonal of a rhombus through a side and an angle: when the sides and one of the angles of a rhombus are known, the following formulas are used: Through a side and a half angle:

Through the side and the other diagonal:

The sum of the squares of the diagonals is equal to the square of the side multiplied by four D^2+d^2=4a^2. From this we can conclude that:

Through a corner and another diagonal:

Through area and another diagonal: the traditional formula for finding the area of ​​a rhombus is S=a*h. But relative to the diagonals it will look like S=1/2*D*d. After transformations we get:

Through the perimeter and another diagonal. In this case, we will derive the formula ourselves. Because A rhombus has equal sides; to find one of them, we divide the perimeter by 4: a=P/4. The diagonals are perpendicular to each other and form a right angle. Then one of the sides and half the lengths of the diagonals form a right triangle. Next, we will use the Pythagorean theorem. For a large diagonal it will look like: D=2*(a^2-(d/2)^2)^1/2. Similarly for finding the small diagonal: d=2*(a^2-(D/2)^2)^1/2.

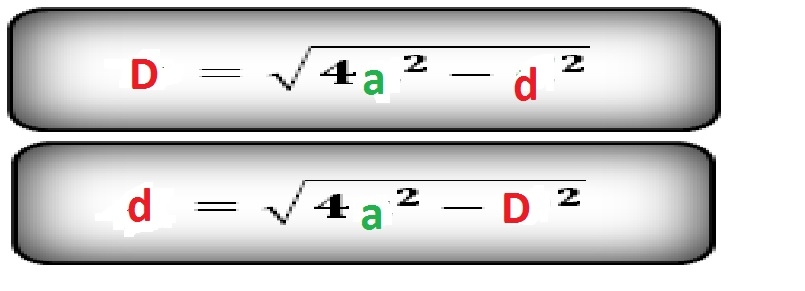
Find the minor diagonal of a rhombus if the perimeter is 20 cm, the major diagonal is 8 cm.

Given: Р=20cm, D=8 cm. Let's find the length of one side of the rhombus by dividing the perimeter into four a=20/4=5 cm. Let's use the formula of point No. 3 and get d=(4*5^2-8^2) ^1/2=6 cm.

Despite the apparent simplicity of such a geometric figure as a rhombus, it is fraught with many interesting aspects. The properties of a parallelogram, bisector, right-angled, and sometimes isosceles triangle are applicable to it. Knowing the formulas, you can easily solve problems of finding the diagonals of a rhombus.

Definition

A rhombus is a quadrilateral with all sides equal.

Comment

A rhombus is a special case of a parallelogram, since its opposite sides are equal in pairs (third feature).

Comment

A rhombus inherits all the properties of a parallelogram.

Properties of a rhombus

The diagonals of a rhombus are mutually perpendicular.

The diagonals of a rhombus are the bisectors of its angles.

Proof

Consider a rhombus $ABCD$ in which the diagonals $AC$ and $BD$ intersect at point $O$.

Let us prove that they are perpendicular and are bisectors of the angles of the rhombus.

Indeed, since $ABCD$ – special case parallelogram, then the diagonals are divided in half by the point of intersection, that is, $AO=OC, BO=OD$.

Then, since $AB=BC=CD=DA$, then $\triangle AOB=\triangle BOC=\triangle COD=\triangle AOD$ by the third equality criterion.

Then $\angle 1=\angle 2=90^\circ$, since these are adjacent angles.

In addition, $\angle 3=\angle 4=\angle 5=\angle 6$, $\angle 7=\angle 8=\angle 9=\angle 10$.

Thus, the diagonals are perpendicular and are bisectors of the angles of the rhombus.

Consequence

The diagonals of a rhombus divide it into four equal right triangles.

Signs of a diamond

If the diagonals of a parallelogram are mutually perpendicular, then this parallelogram is a rhombus.

If one of the diagonals of a parallelogram is the bisector of its angle, then this parallelogram is a rhombus.

If in a quadrilateral $ABCD$ the diagonal $AC$ is the bisector of the angles $\angle A$ and $\angle C$, and the diagonal $BD$ is the bisector of the angles $B$ and $D$, then $ABCD$ is a rhombus.

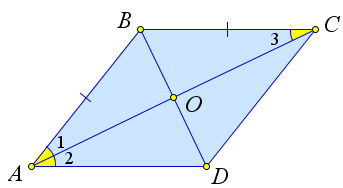
Proof

Let us prove the first point of the theorem.

Consider a parallelogram $ABCD$ in which $AC\perp BD$.

Let us prove that $ABCD$ is a rhombus.

In a parallelogram, the diagonals are bisected by the point of intersection, hence $AO=OC, BO=OD$.

Also, $\angle 1=\angle 2=90^\circ$.

Then $\triangle AOB=\triangle AOD$ by the first equality criterion.

Therefore $AB=AD$.

And since $ABCD$ is a parallelogram, then $BC=AD=AB=CD$, that is, $ABCD$ is a rhombus.

Let us prove the second point of the theorem.

Consider the parallelogram $ABCD$, in which the diagonal $AC$ is the bisector of the angle $\angle A$, that is, $\angle 1=\angle 2$.

Let us prove that $ABCD$ is a rhombus.

$\angle 2=\angle 3$, lying crosswise, therefore, $\angle 1=\angle 3$.

That is, $\triangle ABC$ is isosceles and $AB=BC$.

And since $ABCD$ is a parallelogram, then $AB=CD, BC=AD$, that is, $AB=BC=CD=AD$, and $ABCD$ is a rhombus.

Let us prove the third point of the theorem

Note that $\triangle ABC=\triangle ADC$ by the second criterion ($\angle 1=\angle 2, \angle 3=\angle 4$, $AC$ – general).

Then $\angle B=\angle D$, and therefore their halves are equal: $\angle 5=\angle 6=\angle7=\angle 8$.

But then the triangles $\triangle ABD$ and $\triangle BCD$ are isosceles: $AB=AD, BC=CD$.

In addition, $\triangle ABD=\triangle BCD$ by the second criterion ($BD$ – general, $\angle 5=\angle6, \angle 7=\angle 8$).

This means $AB=BC$ and $AD=CD$.

Thus, all sides of the quadrilateral are equal to each other: $AB=BC=CD=DA$.