A parallelogram is a quadrilateral that has opposite sides parallel, i.e. lie on parallel lines

Properties of a parallelogram: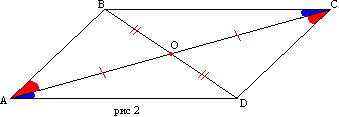
Theorem 22. Opposite sides of a parallelogram are equal.
Proof. In the parallelogram ABCD we draw a diagonal AC. Triangles ACD and ACB are congruent, as having a common side AC and two pairs of equal angles. adjacent to it: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (as crosswise angles with parallel lines AD and BC). This means that AB = CD and BC = AD, as the corresponding sides of equal triangles, etc. From the equality of these triangles it also follows that the corresponding angles of the triangles are equal:
Theorem 23. The opposite angles of the parallelogram are equal: ∠ A=∠ C and ∠ B=∠ D.
The equality of the first pair comes from the equality of triangles ABD and CBD, and the second - ABC and ACD.
Theorem 24. Adjacent angles of a parallelogram, i.e. angles adjacent to one side add up to 180 degrees.
This is so because they are interior one-sided angles.
Theorem 25. The diagonals of a parallelogram bisect each other at their intersection point.
Proof. Consider triangles BOC and AOD. According to the first property AD=BC ∠ OAD=∠ OCB and ∠ ODA=∠ OBC lying crosswise for parallel lines AD and BC. Therefore, triangles BOC and AOD are equal in side and adjacent angles. This means BO=OD and AO=OS, like the corresponding sides of equal triangles, etc.

Signs of a parallelogram
Theorem 26. If the opposite sides of a quadrilateral are equal in pairs, then it is a parallelogram.
Proof. Let the quadrilateral ABCD have sides AD and BC, AB and CD respectively equal (Fig. 2). Let's draw the diagonal AC. Triangles ABC and ACD are equal on three sides. Then angles BAC and DCA are equal and, therefore, AB is parallel to CD. The parallelism of sides BC and AD follows from the equality of angles CAD and ACB.
Theorem 27. If the opposite angles of a quadrilateral are equal in pairs, then it is a parallelogram.
Let ∠ A=∠ C and ∠ B=∠ D. Because ∠ A+∠ B+∠ C+∠ D=360 o, then ∠ A+∠ B=180 o and sides AD and BC are parallel (based on the parallelism of straight lines). We will also prove the parallelism of sides AB and CD and conclude that ABCD is a parallelogram by definition.
Theorem 28. If adjacent corners of a quadrilateral, i.e. The angles adjacent to one side add up to 180 degrees, then it is a parallelogram.
If the interior one-sided angles add up to 180 degrees, then the straight lines are parallel. So AB is parallel to CD and BC is parallel to AD. A quadrilateral turns out to be a parallelogram by definition.
Theorem 29. If the diagonals of a quadrilateral bisect each other at the point of intersection, then the quadrilateral is a parallelogram.
Proof. If AO = OC, BO = OD, then triangles AOD and BOC are equal, as having equal (vertical) angles at vertex O, enclosed between pairs of equal sides. From the equality of triangles we conclude that AD and BC are equal. The sides AB and CD are also equal, and the quadrilateral turns out to be a parallelogram according to criterion 1.
Theorem 30. If a quadrilateral has a pair of equal, parallel sides, then it is a parallelogram.
Let the sides AB and CD of quadrilateral ABCD be parallel and equal. Let's draw diagonals AC and BD. From the parallelism of these lines it follows that the crosswise angles ABO = CDO and BAO = OCD are equal. Triangles ABO and CDO are equal in side and adjacent angles. Therefore AO=OS, VO=ОD, i.e. The diagonals are divided in half by the intersection point and the quadrilateral turns out to be a parallelogram according to criterion 4.

In geometry, special cases of parallelograms are considered.

1. Definition of a parallelogram.

If we intersect a pair of parallel lines with another pair of parallel lines, we get a quadrilateral whose opposite sides are parallel in pairs.

In quadrilaterals ABDC and EFNM (Fig. 224) ВD || AC and AB || CD;

EF || MN and EM || FN.

A quadrilateral whose opposite sides are parallel in pairs is called a parallelogram.

2. Properties of a parallelogram.

Theorem. The diagonal of a parallelogram divides it into two equal triangles.

Let there be a parallelogram ABDC (Fig. 225), in which AB || CD and AC || ВD.

You need to prove that the diagonal divides it into two equal triangles.

Let us draw diagonal CB in parallelogram ABDC. Let us prove that \(\Delta\)CAB = \(\Delta\)СДВ.

Side NE is common to these triangles; ∠ABC = ∠BCD, as internal crosswise angles with parallel AB and CD and secant CB; ∠ACB = ∠СВD, also like internal crosswise angles with parallel AC and BD and secant CB.

Hence \(\Delta\)CAB = \(\Delta\)СДВ.

In the same way, one can prove that the diagonal AD will divide the parallelogram into two equal triangles ACD and ABD.

Consequences:

1 . Opposite angles of a parallelogram are equal to each other.

∠A = ∠D, this follows from the equality of triangles CAB and CDB.

Likewise, ∠C = ∠B.

2. The opposite sides of a parallelogram are equal to each other.

AB = CD and AC = BD, since these are sides of equal triangles and lie opposite equal angles.

Theorem 2. The diagonals of a parallelogram are divided in half at the point of their intersection.

Let BC and AD be the diagonals of the parallelogram ABC (Fig. 226). Let us prove that AO = OD and CO = OB.

To do this, compare some pair of oppositely located triangles, for example \(\Delta\)AOB and \(\Delta\)COD.

In these triangles AB = CD, like opposite sides of a parallelogram;

∠1 = ∠2, as internal angles lying crosswise with parallel AB and CD and secant AD;

∠3 = ∠4 for the same reason, since AB || CD and SV are their secants.

It follows that \(\Delta\)AOB = \(\Delta\)СOD. And in equal triangles, equal sides lie opposite equal angles. Therefore, AO = OD and CO = OB.

Theorem 3. The sum of the angles adjacent to one side of a parallelogram is equal to 180°.

In the parallelogram ABCD we draw the diagonal AC and get two triangles ABC and ADC.

The triangles are equal, since ∠1 = ∠4, ∠2 = ∠3 (crossing angles of parallel lines), and side AC is common.
From the equality \(\Delta\)ABC = \(\Delta\)ADC it follows that AB = CD, BC = AD, ∠B = ∠D.

The sum of angles adjacent to one side, for example angles A and D, is equal to 180° as one-sided angles for parallel lines.

A parallelogram is a quadrilateral whose opposite sides are parallel in pairs. The following figure shows parallelogram ABCD. It has side AB parallel to side CD and side BC parallel to side AD.

As you may have guessed, a parallelogram is a convex quadrilateral. Let's consider the basic properties of a parallelogram.

Properties of a parallelogram

1. In a parallelogram, opposite angles and opposite sides are equal. Let's prove this property - consider the parallelogram presented in the following figure.

Diagonal BD divides it into two equal triangles: ABD and CBD. They are equal along the side BD and the two angles adjacent to it, since the angles lying crosswise at the secant BD of parallel lines BC and AD and AB and CD, respectively. Therefore AB = CD and
BC = AD. And from the equality of angles 1, 2,3 and 4 it follows that angle A = angle1 + angle3 = angle2 + angle4 = angle C.

2. The diagonals of a parallelogram are divided in half by the point of intersection. Let point O be the intersection point of diagonals AC and BD of parallelogram ABCD.

Then triangle AOB and triangle COD are equal to each other, along the side and two adjacent angles. (AB = CD since these are opposite sides of the parallelogram. And angle1 = angle2 and angle3 = angle4 are like crosswise angles when the lines AB and CD intersect with the secants AC and BD, respectively.) From this it follows that AO = OC and OB = OD, which and needed to be proven.

All main properties are illustrated in the following three figures.

Lesson summary.

Algebra 8th grade

Teacher Sysoy A.K.

School 1828

Lesson topic: “Parallelogram and its properties”

Lesson type: combined

Lesson objectives:

1) Ensure the assimilation of a new concept - a parallelogram and its properties

2) Continue developing the skills and abilities to solve geometric problems;

3) Development of a culture of mathematical speech

Lesson plan:

1. Organizing time

(Slide 1)

The slide shows a statement by Lewis Carroll. Students are informed about the purpose of the lesson. The readiness of students for the lesson is checked.

2. Updating knowledge

(Slide 2)

On the board are tasks for oral work. The teacher invites students to think about these problems and raise their hands to those who understand how to solve the problem. After solving two problems, a student is called to the board to prove the theorem on the sum of angles, who independently makes additional constructions on the drawing and proves the theorem orally.

Students use the formula for the sum of the angles of a polygon:

3. Main part

(Slide 3)

Definition of a parallelogram on the board. The teacher talks about a new figure and formulates a definition, making the necessary explanations using a drawing. Then, on the checkered part of the presentation, using a marker and ruler, he shows how to draw a parallelogram (several cases are possible)

(Slide 4)

The teacher formulates the first property of a parallelogram. Invites students to tell from the drawing what is given and what needs to be proven. After this, the given task appears on the board. Students guess (maybe with the help of the teacher) that the required equalities must be proven through the equalities of triangles, which can be obtained by drawing a diagonal (a diagonal appears on the board). Next, students guess why the triangles are equal and name the sign that triangles are equal (the corresponding shape appears). They verbally communicate the facts that are necessary to make the triangles equal (as they name them, a corresponding visualization appears). Next, students formulate the property of congruent triangles, it appears as point 3 of the proof, and then independently complete the proof of the theorem orally.

(Slide 5)

The teacher formulates the second property of a parallelogram. A drawing of a parallelogram appears on the board. The teacher suggests using the picture to tell what is given and what needs to be proven. After students correctly report what is given and what needs to be proven, the condition of the theorem appears. Students guess that the equality of the parts of the diagonals can be proven through the equality of trianglesAOB And C.O.D.. Using the previous property of a parallelogram, one guesses that the sides are equalAB And CD. Then they understand that they need to find equal angles and, using the properties of parallel lines, prove the equality of angles adjacent to equal sides. These stages are visualized on the slide. The truth of the theorem follows from the equality of the triangles - the students say it and a corresponding visualization appears on the slide.

(Slide 6)

The teacher formulates the third property of a parallelogram. Depending on the time remaining until the end of the lesson, the teacher can give the students the opportunity to prove this property on their own, or limit themselves to its formulation, and leave the proof itself to the students as homework. The proof can be based on the sum of the angles of an inscribed polygon, which was repeated at the beginning of the lesson, or on the sum of the internal one-sided angles of two parallel linesAD And B.C., and a secant, for exampleAB.

4. Fixing the material

At this stage, students use previously learned theorems to solve problems. Students select ideas for solving the problem independently. Because possible options There is a lot of design and they all depend on how the students will look for a solution to the problem, there is no visualization of the solution to the problems, and the students independently draw up each stage of the solution on a separate board with recording the solution in a notebook.

(Slide 7)

The task condition appears. The teacher suggests formulating “Given” according to the condition. After the students correctly compose a short statement of the condition, “Given” appears on the board. The process for solving the problem might look like this:

Let's draw the height BH (visualized)

Triangle AHB is a right triangle. Angle A equal to angle C and equals 30 0 (according to the property of opposite angles in a parallelogram). 2BH =AB (by the property of the leg lying opposite the 30 0 angle in a right triangle). So AB = 13 cm.

AB = CD, BC = AD (according to the property of opposite sides in a parallelogram) So AB = CD = 13 cm. Since the perimeter of the parallelogram is 50 cm, then BC = AD = (50 – 26): 2 = 12 cm.

Answer: AB = CD = 13 cm, BC = AD = 12 cm.

(Slide 8)

The task condition appears. The teacher suggests formulating “Given” according to the condition. Then “Given” appears on the screen. Using red lines, a quadrilateral is highlighted, about which you need to prove that it is a parallelogram. The process for solving the problem might look like this:

Because BK and MD are perpendicular to one line, then lines BK and MD are parallel.

Through adjacent angles it can be shown that the sum of the internal one-sided angles at straight lines BM and KD and the secant MD is equal to 180 0. Therefore, these lines are parallel.

Since the quadrilateral BMDK has opposite sides parallel in pairs, then this quadrilateral is a parallelogram.

5. End of the lesson. Behavior of the results.

(Slide 8)

Questions on the new topic appear on the slide, to which students answer.