Lesson topic

• Properties of the diagonals of a parallelogram.

Lesson Objectives

• Get acquainted with new definitions and remember some already studied.
• State and prove the property of the diagonals of a parallelogram.
• Learn to apply the properties of shapes when solving problems.
• Developmental – to develop students’ attention, perseverance, perseverance, logical thinking, mathematical speech.
• Educational - through the lesson, cultivate an attentive attitude towards each other, instill the ability to listen to comrades, mutual assistance, and independence.

Lesson Objectives

• Test students' problem-solving skills.

Lesson Plan

1. Introduction.
2. Repetition of previously studied material.
3. Parallelogram, its properties and features.
4. Examples of tasks.
5. Self-check.

Introduction

“A major scientific discovery provides a solution to a major problem, but in the solution of any problem there is a grain of discovery.”

Property of opposite sides of a parallelogram

A parallelogram has opposite sides that are equal.

Proof.

Let ABCD be the given parallelogram. And let its diagonals intersect at point O.
Since Δ AOB = Δ COD by the first criterion of equality of triangles (∠ AOB = ∠ COD, as vertical ones, AO=OC, DO=OB, by the property of the diagonals of a parallelogram), then AB=CD. In the same way, from the equality of triangles BOC and DOA, it follows that BC = DA. The theorem is proven.

Property of opposite angles of a parallelogram

In a parallelogram, opposite angles are equal.

Proof.

Let ABCD be the given parallelogram. And let its diagonals intersect at point O.
From what was proven in the theorem about the properties of the opposite sides of a parallelogram Δ ABC = Δ CDA on three sides (AB=CD, BC=DA from what was proven, AC – general). From the equality of triangles it follows that ∠ ABC = ∠ CDA.
It is also proved that ∠ DAB = ∠ BCD, which follows from ∠ ABD = ∠ CDB. The theorem is proven.

Property of the diagonals of a parallelogram

The diagonals of a parallelogram intersect and are bisected at the point of intersection.

Proof.

Let ABCD be the given parallelogram. Let's draw the diagonal AC. Let's mark the middle O on it. On the continuation of the segment DO, we'll put aside the segment OB 1 equal to DO.
By the previous theorem, AB 1 CD is a parallelogram. Therefore, line AB 1 is parallel to DC. But through point A only one line parallel to DC can be drawn. This means that line AB 1 coincides with line AB.
It is also proved that BC 1 coincides with BC. This means that point C coincides with C 1. parallelogram ABCD coincides with parallelogram AB 1 CD. Consequently, the diagonals of the parallelogram intersect and are bisected at the point of intersection. The theorem is proven.

In textbooks for regular schools(for example, in Pogorelov) it is proven like this: the diagonals divide the parallelogram into 4 triangles. Let's look at one pair and find out - they are equal: their bases are - opposite sides, the corresponding angles adjacent to it are equal as vertical angles for parallel lines. That is, the segments of the diagonals are equal in pairs. All.

Is that all?
It was proven above that the intersection point bisects the diagonals - if it exists. The above reasoning does not prove its very existence in any way. That is, part of the theorem “the diagonals of a parallelogram intersect” remains unproven.

The funny thing is that this part is much harder to prove. This follows, by the way, from a more general result: any convex quadrilateral will have diagonals intersecting, but any non-convex quadrilateral will not.

On the equality of triangles along a side and two adjacent angles (the second sign of equality of triangles) and others.

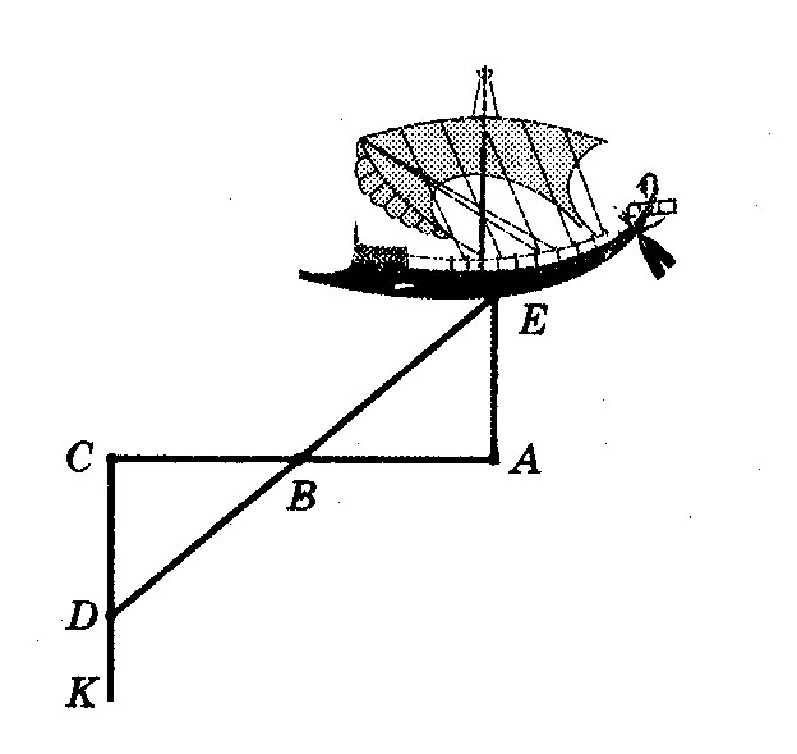
Thales found an important theorem on the equality of two triangles along a side and two adjacent angles practical use. A rangefinder was built in the harbor of Miletus to determine the distance to a ship at sea. It consisted of three driven pegs A, B and C (AB = BC) and a marked straight line SC, perpendicular to CA. When a ship appeared on the SK straight line, we found point D such that points D, .B and E were on the same straight line. As is clear from the drawing, the distance CD on the ground is the desired distance to the ship.

Questions

1. Are the diagonals of a square divided in half by the point of intersection?
   
2. Are the diagonals of a parallelogram equal?
3. Are the opposite angles of a parallelogram equal?
4. State the definition of a parallelogram?
5. How many signs of a parallelogram?
   
6. Can a rhombus be a parallelogram?
   

List of sources used

1. Kuznetsov A.V., mathematics teacher (grades 5-9), Kyiv
2. "Single State exam 2006. Mathematics. Educational and training materials for preparing students / Rosobrnadzor, ISOP - M.: Intellect-Center, 2006"
3. Mazur K. I. “Solving the main competition problems in mathematics of the collection edited by M. I. Skanavi”
4. L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, E. G. Poznyak, I. I. Yudina “Geometry, 7 – 9: textbook for educational institutions”

We worked on the lesson

Kuznetsov A.V.

Poturnak S.A.

Evgeniy Petrov

You can raise a question about modern education, express an idea or solve a pressing problem at Educational forum, where an educational council of fresh thought and action meets internationally. Having created blog, You will not only improve your status as a competent teacher, but also make a significant contribution to the development of the school of the future. Guild of Educational Leaders opens doors to top-ranking specialists and invites them to cooperate in creating the best schools in the world.

A quadrilateral whose opposite sides are parallel is a parallelogram. Diagonals are straight lines connecting opposite vertices. The point of their intersection is the center of symmetry. In general, a parallelogram has two diagonals, D is the long one and d is the short one.

Find the diagonal of a parallelogram using the cosine theorem

• The value of the cosines of the parallelogram angles α and β.

D = √a^2 + b^2 — 2ab cosβ

d = √a^2 + b^2 + 2ab cosβ

D = √a^2 + b^2 + 2ab cosα

d = √a^2 + b^2 — 2ab cosα

Find the diagonal of a parallelogram using one known diagonal and sides

To use this method you need to know:

• The lengths of the sides of the parallelogram a and b.

D = √2a^2 + 2b^2 — d^2

To use this method you need to know:

• Area of ​​a parallelogram.
• The length of one of the diagonals D or d.
• The angle between the diagonals γ or δ.

D = 2S/d sinγ = 2S/d sinδ

d = 2S/D sinγ = 2S/D sinδ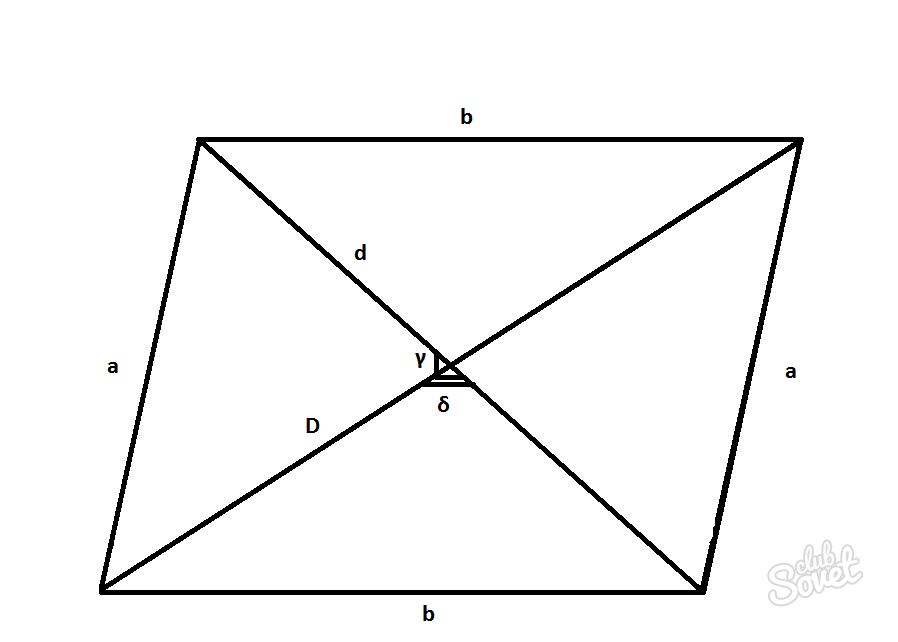

A special case of determining the length of the diagonal of a parallelogram is a square

A square is a parallelogram in which all sides are equal and the angles are 90°. The lengths of the diagonals in this case will be equal to D=d and can be calculated using the Pythagorean theorem.
D=d=a*√2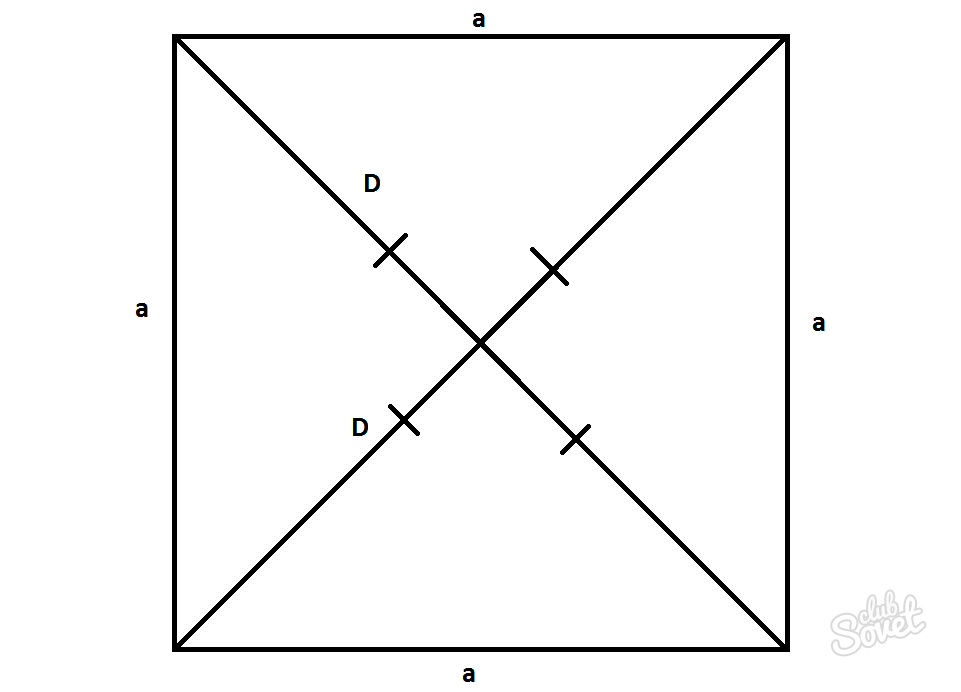

A special case of determining the length of the diagonal of a parallelogram is a rectangle

A rectangle is a parallelogram in which the angles are equal and equal to 90°. The lengths of the diagonals in this case will be equal to D=d and can be calculated using the Pythagorean theorem.
D=d=√(a^2+b^2)

A parallelogram is a quadrilateral whose opposite sides are parallel in pairs.

This definition is already sufficient, since the remaining properties of the parallelogram follow from it and are proved in the form of theorems.

• The main properties of a parallelogram are:
• a parallelogram is a convex quadrilateral;
• A parallelogram has opposite sides that are equal in pairs;
• In a parallelogram, opposite angles are equal in pairs;

The diagonals of a parallelogram are divided in half by the point of intersection.

Parallelogram - convex quadrilateral Let us first prove the theorem that. A polygon is convex if whichever side of it is extended to a straight line, all other sides of the polygon will be on the same side of this straight line.

Let a parallelogram ABCD be given, in which AB is the opposite side for CD, and BC is the opposite side for AD. Then from the definition of a parallelogram it follows that AB || CD, BC || A.D.

Parallel segments have no common points and do not intersect. This means that CD lies on one side of AB. Since segment BC connects point B of segment AB with point C of segment CD, and segment AD connects other points AB and CD, segments BC and AD also lie on the same side of line AB where CD lies. Thus, all three sides - CD, BC, AD - lie on the same side of AB.

Similarly, it is proved that in relation to the other sides of the parallelogram, the other three sides lie on the same side.

Opposite sides and angles are equal

One of the properties of a parallelogram is that In a parallelogram, opposite sides and opposite angles are equal in pairs. For example, if a parallelogram ABCD is given, then it has AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. This theorem is proven as follows.

A parallelogram is a quadrilateral. This means it has two diagonals. Since a parallelogram is a convex quadrilateral, any of them divides it into two triangles. In the parallelogram ABCD, consider the triangles ABC and ADC obtained by drawing the diagonal AC.

These triangles have one side in common - AC. Angle BCA equal to angle CAD as vertical with parallel BC and AD. Angles BAC and ACD are also equal to vertical angles when AB and CD are parallel. Therefore, ∆ABC = ∆ADC at two angles and the side between them.

In these triangles, side AB corresponds to side CD, and side BC corresponds to AD. Therefore, AB = CD and BC = AD.

Angle B corresponds to angle D, i.e. ∠B = ∠D. Angle A of a parallelogram is the sum of two angles - ∠BAC and ∠CAD. Angle C is equal to ∠BCA and ∠ACD. Since pairs of angles are equal to each other, then ∠A = ∠C.

Thus, it is proven that in a parallelogram opposite sides and angles are equal.

Diagonals are divided in half

Since a parallelogram is a convex quadrilateral, it has two diagonals, and they intersect. Let parallelogram ABCD be given, its diagonals AC and BD intersect at point E. Consider the triangles ABE and CDE formed by them.

These triangles have sides AB and CD equal to the opposite sides of a parallelogram. Angle ABE is equal to angle CDE as crosswise lying with parallel lines AB and CD. For the same reason, ∠BAE = ∠DCE. This means ∆ABE = ∆CDE at two angles and the side between them.

You can also notice that angles AEB and CED are vertical and therefore also equal to each other.

Since triangles ABE and CDE are equal to each other, then all their corresponding elements are equal. Side AE ​​of the first triangle corresponds to side CE of the second, which means AE = CE. Similarly BE = DE. Each pair of equal segments constitutes a diagonal of a parallelogram. Thus it is proven that The diagonals of a parallelogram are bisected by their intersection point.