In this part we will discuss the circle circumscribed around (often said "about") a triangle. First of all, let's give a definition.

1. Existence and circumcircle center

Here the question arises: does such a circle exist for every triangle? It turns out that yes, for everyone. And moreover, we will now formulate a theorem that also answers the question of where the center of the circumscribed circle is located.

Look, like this:

Let's be brave and prove this theorem. If you have already read the topic “” and understood why three bisectors intersect at one point, then it will be easier for you, but if you haven’t read it, don’t worry: now we’ll figure it out.

We will carry out the proof using the concept of locus of points (GLP).

Well, for example, is the set of balls the “geometric locus” of round objects? No, of course, because there are round...watermelons. Is it a set of people, a “geometric place”, who can speak? No, either, because there are babies who cannot speak. In life, it is generally difficult to find an example of a real “geometric location of points.” It's easier in geometry. Here, for example, is exactly what we need:

Here the set is the perpendicular bisector, and the property “ ” is “to be equidistant (a point) from the ends of the segment.”

Shall we check? So, you need to make sure of two things:

Let's connect c and c.Then the line is the median and height b. This means - isosceles - we made sure that any point lying on the perpendicular bisector is equally distant from the points and.

Let's take the middle and connect and. The result is the median. But, according to the condition, not only the median is isosceles, but also the height, that is, the perpendicular bisector. This means that the point exactly lies on the perpendicular bisector.

All! We have fully verified the fact that the perpendicular bisector to a segment is the locus of points equidistant from the ends of the segment.

This is all well and good, but have we forgotten about the circumscribed circle? Not at all, we have just prepared ourselves a “springboard for attack.”

Consider a triangle. Let's draw two bisectoral perpendiculars and, say, to the segments and. They will intersect at some point, which we will name.

Now, pay attention!

The point lies on the perpendicular bisector;
the point lies on the perpendicular bisector.
And that means, and.

Several things follow from this:

Firstly, the point must lie on the third bisector perpendicular to the segment.

That is, the perpendicular bisector must also pass through the point, and all three perpendicular bisectors intersect at one point.

Secondly: if we draw a circle with a center at a point and a radius, then this circle will also pass through both the point and the point, that is, it will be a circumscribed circle. This means that it already exists that the intersection of three perpendicular bisectors is the center of the circumscribed circle for any triangle.

And the last thing: about uniqueness. It is clear (almost) that the point can be obtained in a unique way, therefore the circle is unique. Well, we’ll leave “almost” for your reflection. So we proved the theorem. You can shout “Hurray!”

What if the problem asks “find the radius of the circumscribed circle”? Or vice versa, the radius is given, but you need to find something else? Is there a formula that relates the radius of the circumcircle to the other elements of the triangle?

Definition

A circle \(S\) is circumscribed about a polygon \(P\) if all the vertices of the polygon \(P\) lie on the circle \(S\) .

In this case, the polygon \(P\) is said to be inscribed in a circle.

Definition

The perpendicular bisector of a segment is a line passing through the middle of a given segment perpendicular to it.

Theorem

Each point of the perpendicular bisector of a segment is equidistant from the ends of that segment.

Proof

Consider the segment \(AB\) and the perpendicular bisector \(a\) to it. Let us prove that for any point \(X\in a\) the following holds: \(AX=BX\) .

Consider \(\triangle AXB\) : the segment \(XO\) is the median and altitude, therefore \(\triangle AXB\) is isosceles, therefore \(AX=BX\) .

Theorem

The perpendicular bisectors to the sides of a triangle intersect at one point.

Proof

Consider \(\triangle ABC\) . Let's draw perpendicular bisectors to the sides \(AB\) and \(AC\). They will intersect at the point \(O\) .

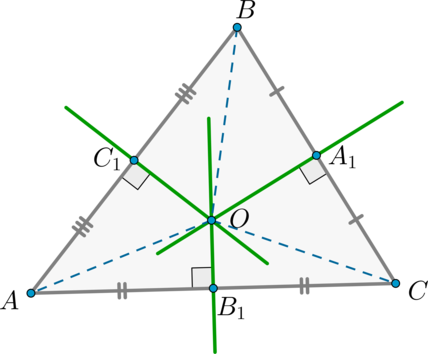
According to the previous theorem, for the perpendicular bisector \(C_1O\) the following holds: \(AO=BO\) , and for \(B_1O\) - \(AO=CO\) . Therefore, \(BO=CO\) . This means that \(\triangle BOC\) is isosceles, therefore, the height \(OA_1\) drawn to the base \(BC\) will also be the median. This means that \(OA_1\) is the perpendicular bisector to the segment \(BC\) .

Thus, all three perpendicular bisectors intersect at one point \(O\) .

Consequence

If a point is equidistant from the ends of a segment, then it lies on its perpendicular bisector.

Theorem

A single circle can be circumscribed around any triangle, and the center of the circumscribed circle is the point of intersection of the perpendicular bisectors to the sides of the triangle.

Proof

From the theorem proven above it follows that \(AO=BO=CO\) . This means that all the vertices of the triangle are equidistant from the point \(O\), therefore, they lie on the same circle.

There is only one such circle. Let us assume that another circle can be described around \(\triangle ABC\). Then its center should coincide with the point \(O\) (since this is the only point equidistant from the vertices of the triangle), and the radius should be equal to the distance from the center to some of the vertices, i.e. \(OA\) . Because If these circles have the same center and radius, then these circles also coincide.

Inscribed triangle area theorem

If \(a, b, c\) – sides of the triangle, and \(R\) is the radius of the circle circumscribed around it, then the area of ​​the triangle \

Proof*
It is recommended that you familiarize yourself with the proof of this theorem after studying the topic “Theorem of Sines”.

Let's denote the angle between sides \(a\) and \(c\) as \(\alpha\) . Then \(S_(\triangle)=\frac12 ac\cdot \sin \alpha\).

By the theorem of sines \(\dfrac b(\sin\alpha)=2R\) , whence \(\sin \alpha=\dfrac b(2R)\) . Hence, \(S_(\triangle)=\dfrac(abc)(4R)\).

Theorem

A circle can be described around a quadrilateral if and only if the sum of its opposite angles is equal to \(180^\circ\) .

Proof

Necessity.

If a circle can be described around a quadrilateral \(ABCD\), then \(\buildrel\smile\over(ABC) + \buildrel\smile\over(ADC) = 360^\circ\), where \(\angle ABC + \angle ADC = \frac(1)(2)\buildrel\smile\over(ABC) + \frac(1)(2)\buildrel\smile\over(ADC) = \frac(1 )(2)(\buildrel\smile\over(ABC) + \buildrel\smile\over(ADC)) = 180^\circ\). For angles \(BCD\) and \(BAD\) it is similar.

Adequacy.

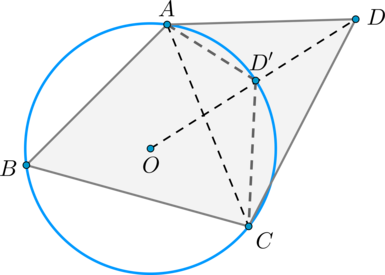
Let us describe a circle around the triangle \(ABC\) . Let the center of this circle be the point \(O\) . On the line passing through the points \(O\) and \(D\), we mark the point \(D"\) of intersection of this line and the circle. Let us assume that the points \(D\) and \(D"\) do not coincide, then consider the quadrilateral \(CD"AD\) .

Angles \(CD"A\) and \(CDA\) complement angle \(ABC\) to \(180^\circ\) (\(\angle CDA\) complements by condition, and \(\angle CD"A \) as proven above), therefore, they are equal, but then the sum of the angles of the quadrilateral \(AD"CD\) is greater than \(360^\circ\), which cannot be (the sum of the angles of this quadrilateral is the sum of the angles of two triangles), therefore, the points \(D\) and \(D"\) coincide.

Comment. In the figure, the point \(D\) lies outside the circle bounded by the circle circumscribed by \(\triangle ABC\), however, in the case when \(D\) lies inside, the proof also remains valid.

Theorem

A circle can be described around a convex quadrilateral \(ABCD\) if and only if \(\angle ABD=\angle ACD\) .

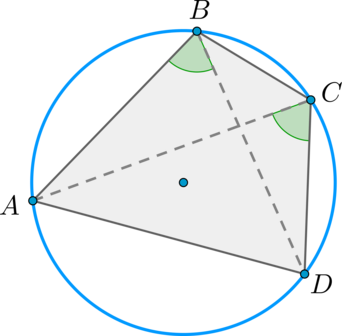
Proof

Necessity. If a circle is circumscribed around \(ABCD\), then the angles \(\angle ABD\) and \(\angle ACD\) are inscribed and rest on one arc \(\buildrel\smile\over(AD)\), therefore, they are equal.

Adequacy. Let \(\angle ABD=\angle ACD=\alpha\). Let us prove that a circle can be described around \(ABCD\).

Let's describe a circle around \(\triangle ABD\) . Let the straight line \(CD\) intersect this circle at the point \(C"\). Then \(\angle ABD=\angle AC"D \Rightarrow \angle AC"D=\angle ACD\).

Hence, \(\angle CAD=\angle C"AD=180^\circ-\angle ADC-\angle AC"D\), that is \(\triangle AC"D=\triangle ACD\) along a common side \(AD\) and two adjacent angles (\(\angle C"AD=\angle CAD\) , \(\angle ADC"=\angle ADC\) – common). This means \(DC"=DC\), that is, the points \(C"\) and \(C\) coincide.

Theorems

1. If a circle is circumscribed around a parallelogram, then it is a rectangle (Fig. 1).

2. If a circle is described around a rhombus, then it is a square (Fig. 2).

3. If a circle is described around a trapezoid, then it is isosceles (Fig. 3).

The converse statements are also true: around a rectangle, rhombus and isosceles trapezoid, one can describe a circle, and only one.

Proof

1) Let a circle be circumscribed around the parallelogram \(ABCD\). Then the sums of its opposite angles are equal \(180^\circ: \quad \angle A+\angle C=180^\circ\). But in a parallelogram, opposite angles are equal, because \(\angle A=\angle C\) . Hence, \(\angle A=\angle C=90^\circ\). So, by definition, \(ABCD\) is a rectangle.

2) Let a circle be circumscribed around the rhombus \(MNKP\). Similar to the previous point (since a rhombus is a parallelogram), it is proved that \(MNKP\) is a rectangle. But all sides of this rectangle are equal (since it is a rhombus), which means \(MNKP\) is a square.

The opposite statement is obvious.

3) Let a circle be circumscribed around the trapezoid \(QWER\). Then \(\angle Q+\angle E=180^\circ\). But from the definition of a trapezoid it follows that \(\angle Q+\angle W=180^\circ\). Therefore, \(\angle W=\angle E\) . Because the angles at the base \(WE\) of the trapezoid are equal, then it is isosceles.

The opposite statement is obvious.

Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

Below are some examples of the types of personal information we may collect and how we may use such information.

What personal information do we collect:

• When you submit a request on the site, we may collect various information, including your name, telephone number, address Email etc.

How we use your personal information:

• The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
• From time to time, we may use your personal information to send important notices and communications.
• We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
• If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.

Disclosure of information to third parties

We do not disclose the information received from you to third parties.

Exceptions:

• If necessary, in accordance with the law, judicial procedure, in legal proceedings, and/or based on public inquiries or requests from government agencies on the territory of the Russian Federation - disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
• In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.

Respecting your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.

>>Geometry: The circumcircle of a triangle. Complete lessons

LESSON TOPIC: A circle circumscribed around a triangle.

Lesson objectives:

• Deepen your knowledge on the topic “Circle in triangles”

Lesson objectives:

• Systematize knowledge on this topic
• Prepare to solve problems of increased complexity.

Lesson plan:

1. Introduction.
2. Theoretical part.
3. For a triangle.
4. Practical part.

Introduction.

The topic “Inscribed and circumscribed circles in triangles” is one of the most difficult in the geometry course. She spends very little time in class.

Geometric problems of this topic are included in the second part of the exam Unified State Examination work for a high school course.
Successful completion of these assignments requires a solid knowledge of basic geometric facts and some experience in solving geometric problems.

Theoretical part.

Circumference of a polygon- a circle containing all the vertices of a polygon. The center is the point (usually denoted O) of the intersection of the perpendicular bisectors to the sides of the polygon.

Properties.

The circumcenter of a convex n-gon lies at the point of intersection of the perpendicular bisectors to its sides. As a consequence: if a circle is circumscribed next to an n-gon, then all the perpendicular bisectors to its sides intersect at one point (the center of the circle).
A circle can be drawn around any regular polygon.

For a triangle.

A circle is called circumscribed about a triangle if it passes through all its vertices.

A circle can be described around any triangle, and only one. Its center will be the point of intersection of the bisector perpendiculars.

For an acute triangle, the center of the circumscribed circle lies inside, for an obtuse-angled one - outside the triangle, for a rectangular one - at the middle of the hypotenuse.

The radius of the circumcircle can be found using the formulas:

Where:
a,b,c- sides of the triangle,
α - angle opposite side a,
S- area of ​​a triangle.

Prove:

t.O - the point of intersection of the perpendicular bisectors to the sides ΔABC

Proof:

1. ΔAOC - isosceles, because OA=OS (as radii)
2. ΔAOC - isosceles, perpendicular OD - median and height, i.e. so O lies on the perpendicular bisector to side AC
3. It is similarly proved that t.O lies on the perpendicular bisectors to the sides AB and BC

Q.E.D.

Comment.

A straight line passing through the middle of a segment perpendicular to it is often called a perpendicular bisector. In this regard, it is sometimes said that the center of a circle circumscribed about a triangle lies at the intersection of the perpendicular bisectors to the sides of the triangle.