Гіпотенуза трапеції. Трапеція, середня лінія трапеції, трикутник
Якщо в рівнобедреній трапеції діагоналі перпендикулярні, при вирішенні задачі буде корисним наступний теоретичний матеріал.
1. Якщо в рівнобедреній трапеції діагоналі перпендикулярні, висота трапеції дорівнює напівсумі підстав.
Проведемо через точку C пряму CF, паралельну BD, і продовжимо пряму AD до перетину CF.
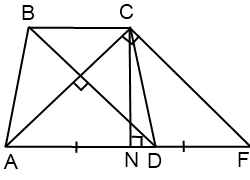
Чотирикутник BCFD — паралелограм (BC DF як основи трапеції, BD CF по побудові). Отже, CF=BD, DF=BC та AF=AD+BC.
Трикутник ACF прямокутний (якщо пряма перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна до іншої прямої). Оскільки в рівнобедреній трапеції діагоналі рівні, а CF = BD, то CF = AC, тобто трикутник ACF - рівнобедрений з основою AF. Значить, його висота CN також медіаною. Оскільки медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює її половині, то
![]()
що в загальному виглядіможна записати як
де h – висота трапеції, a та b – її основи.
2. Якщо в рівнобедреній трапеції діагоналі перпендикулярні, то її висота дорівнює середній лінії.
Оскільки середня лінія трапеції m дорівнює напівсумі основ, то
3. Якщо в рівнобедреній трапеції діагоналі перпендикулярні, то площа трапеції дорівнює квадрату висоти трапеції (або квадрату напівсуми основ або квадрату середньої лінії).
Так як площа трапеції знаходиться за формулою
![]()
а висота, напівсума основ та середня лінія рівнобічної трапеції з перпендикулярними діагоналями рівні між собою:
![]()
Трапеція – це окремий випадокчотирикутника, у якого одна пара сторін є паралельною. Термін «трапеція» походить від грецького словаτράπεζα, що означає "стіл", "столик". У цій статті ми розглянемо види трапеції та її властивості. Крім того, розберемося, як розраховувати окремі елементи цієї, наприклад, діагональ рівнобічної трапеції, середню лінію, площу та ін. Матеріал викладений у стилі елементарної популярної геометрії, тобто в легкодоступній формі.
Загальні відомості
Спочатку давайте розберемося, що таке чотирикутник. Ця фігура є окремим випадком багатокутника, що містить чотири сторони і чотири вершини. Дві вершини чотирикутника, які є сусідніми, називаються протилежними. Те саме можна сказати і про дві несуміжні сторони. Основні види чотирикутників - це паралелограм, прямокутник, ромб, квадрат, трапеція та дельтоїд.
Отже, повернемося до трапецій. Як ми вже говорили, у цієї постаті дві сторони є паралельними. Їх називають основами. Дві інші (непаралельні) – бічні сторони. У матеріалах іспитів та різних контрольних робітдуже часто можна зустріти завдання, пов'язані з трапеціями, вирішення яких найчастіше вимагає від учня знань, не передбачених програмою. Шкільний курс геометрії знайомить учнів із властивостями кутів та діагоналей, а також середньої лінії рівнобедреної трапеції. Але, крім цього, згадана геометрична фігура має й інші особливості. Але про них трохи згодом...
Види трапеції
Існує багато видів цієї постаті. Однак найчастіше прийнято розглядати два з них – рівнобедрену та прямокутну.
1. Прямокутна трапеція - це фігура, у якої одна з бічних сторін перпендикулярна до основ. У неї два кути завжди дорівнюють дев'яноста градусам.
2. Рівностегновий трапеція - це геометрична фігура, у якої бічні сторони рівні між собою. Отже, і кути біля основ також попарно рівні.
Основні принципи методики вивчення властивостей трапеції
До основного принципу можна зарахувати використання так званого задачного підходу. По суті немає необхідності для введення в теоретичний курс геометрії нових властивостей цієї фігури. Їх можна відкривати і формулювати в процесі вирішення різних завдань (краще системних). При цьому дуже важливо, щоб викладач знав, які завдання потрібно поставити перед школярами у той чи інший момент навчального процесу. Більше того, кожна властивість трапеції може бути представлена у вигляді ключового завдання у системі задач.
Другим принципом є так звана спіральна організація вивчення «чудових» властивостей трапеції. Це передбачає повернення в процесі навчання до окремих ознак цієї геометричної фігури. Таким чином, учням легше їх запам'ятовувати. Наприклад, властивість чотирьох точок. Його можна доводити як із вивченні подоби, і згодом з допомогою векторів. А рівновеликість трикутників, прилеглих до боків фігури, можна доводити, застосовуючи як властивості трикутників з рівними висотами, проведеними до сторон, які лежать однією прямої, а й з допомогою формули S= 1/2(ab*sinα). Крім того, можна відпрацювати на вписаній трапеції або прямокутний трикутник на описаній трапеції і т.д.
Застосування «позапрограмних» особливостей геометричної фігури у змісті шкільного курсу – це задачна технологія їхнього викладання. Постійне звернення до властивостей, що вивчаються при проходженні інших тем, дозволяє учням глибше пізнавати трапецію і забезпечує успішність вирішення поставлених завдань. Отже, приступимо до вивчення цієї чудової постаті.

Елементи та властивості рівнобедреної трапеції
Як ми вже зазначали, у цієї геометричної фігури бічні сторони рівні. Ще вона відома як правильна трапеція. А чим же вона така примітна і чому отримала таку назву? До особливостей цієї постаті належить те, у неї рівні як бічні боку й кути біля основ, а й діагоналі. Крім того, сума кутів рівнобедреної трапеції дорівнює 360 градусів. Але це ще не все! З усіх відомих трапецій тільки навколо рівнобедреного можна описати коло. Це пов'язано з тим, що сума протилежних кутів цієї фігури дорівнює 180 градусам, а тільки за такої умови можна описати коло навколо чотирикутника. Наступною властивістю аналізованої геометричної фігури є те, що відстань від вершини основи до проекції протилежної вершини на пряму, яка містить цю основу, дорівнюватиме середньої лінії.
А тепер давайте розберемося, як знайти кути рівнобедреної трапеції. Розглянемо варіант розв'язання цього завдання за умови, що відомі розміри сторін фігури.
Рішення
Зазвичай чотирикутник прийнято позначати літерами А, Б, С, Д, де БС та АТ - це підстави. У рівнобедреній трапеції бічні сторони рівні. Вважатимемо, що й розмір дорівнює Х, а розміри підстав рівні Y і Z (меншого і більшого відповідно). Для проведення обчислення необхідно з кута провести висоту Н. В результаті вийшов прямокутний трикутник АБН, де АБ - гіпотенуза, а БН і АН - катети. Обчислюємо розмір катета АН: від більшої основи забираємо менше, і результат ділимо на 2. Запишемо у вигляді формули: (Z-Y)/2 = F. Тепер для обчислення гострого кута трикутника скористаємося функцією cos. Отримуємо наступний запис: cos(β) = Х/F. Тепер обчислюємо кут: β=arcos (Х/F). Далі, знаючи один кут, ми можемо визначити і другий, для цього чинимо елементарну арифметичну дію: 180 - β. Усі кути визначені.
Існує і друге вирішення цієї задачі. Спочатку опускаємо з кута У висоту Н. Обчислюємо значення катета БН. Нам відомо, що квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів катетів. Отримуємо: БН = √(Х2-F2). Далі використовуємо тригонометричну функцію tg. В результаті маємо: β = arctg (БН/F). Гострий кут знайдено. Далі визначаємо тупий кут аналогічно першому способу.
Властивість діагоналей рівнобедреної трапеції
Спочатку запишемо чотири правила. Якщо діагоналі в рівнобедреній трапеції перпендикулярні, то:
Висота фігури дорівнюватиме сумі підстав, поділеної на дві;
Її висота та середня лінія рівні;
Центр кола є точкою, в якій перетинаються;
Якщо бічний бік ділиться точкою торкання на відрізки Н і М, тоді дорівнює квадратного коренятвори цих відрізків;
Чотирьохкутник, який утворився точками торкання, вершиною трапеції та центром вписаного кола - це квадрат, у якого сторона дорівнює радіусу;
Площа постаті дорівнює добутку підстав та добутку напівсуми підстав на її висоту.
Подібні трапеції
Ця тема дуже зручна для вивчення властивостей цієї прикладу. Наприклад, діагоналі розбивають трапецію на чотири трикутники, причому прилеглі до основ є подібними, а до бічних сторін - рівновеликими. Це твердження можна назвати властивістю трикутників, куди розбита трапеція її діагоналями. Перша частина цього твердження доводиться через ознаку подібності з двох кутів. Для доказу другої частини краще скористатися способом, наведеним нижче.
Доказ теореми
Приймаємо, що фігура АБСД (АТ та БС – основи трапеції) розбивається діагоналями ВД та АС. Точка їх перетину - О. Отримуємо чотири трикутники: АОС - у нижньої основи, БОС - у верхньої основи, АБО та СОД у бокових сторін. Трикутники СОД та БОС мають загальну висоту в тому випадку, якщо відрізки БО та ОД є їх підставами. Отримуємо, що різниця їх площ (П) дорівнює різниці цих відрізків: ПБОС/ПСОД = БО/ОД = К. Отже, ПСОД = ПБОС/К. Аналогічно, трикутники БОС та АОБ мають загальну висоту. Приймаємо за їх підстави відрізки СО та ОА. Отримуємо ПБОС/ПАОБ = СО/ОА = К та ПАОБ = ПБОС/К. На цьому випливає, що ПСОД = ПАОБ.
Для закріплення матеріалу учням рекомендується знайти зв'язок між площами отриманих трикутників, куди розбита трапеція її діагоналями, вирішивши таке завдання. Відомо, що у трикутників БОС та АОД площі рівні, необхідно знайти площу трапеції. Оскільки ПСОД = ПАОБ, отже, ПАБСД = ПБОС+ПАОД+2*ПСОД. З подоби трикутників БОС та АОД випливає, що БО/ОД = √(ПБОС/ПАОД). Отже, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Отримуємо ПСОД = √(ПБОС*ПАОД). Тоді ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.
Властивості подоби
Продовжуючи розвивати цю тему, можна доводити інші цікаві особливостітрапецій. Так, за допомогою подібності можна довести властивість відрізка, який проходить через точку, утворену перетином діагоналей цієї геометричної фігури, паралельно до основ. Для цього розв'яжемо наступне завдання: необхідно знайти довжину відрізка РК, який проходить через точку О. З подоби трикутників АОД і БОС випливає, що АО/ОС=АД/БС. З подоби трикутників АОР і АСБ випливає, що АО/АС=РО/БС=АД/(БС+АД). Звідси отримуємо, що РВ = БС * АТ / (БС + АТ). Аналогічно з подоби трикутників ДОК і ДБС випливає, що ОК = БС * АД / (БС + АД). Звідси отримуємо, що РВ=ОК і РК=2*БС*АД/(БС+АД). Відрізок, що проходить через точку перетину діагоналей, паралельний основам і сполучає дві бічні сторони, ділиться точкою перетину навпіл. Його довжина - це середня гармонійна підстава фігури.
Розглянемо таку якість трапеції, яку називають властивістю чотирьох точок. Точки перетину діагоналей (О), перетину продовження бічних сторін (Е), а також середини основ (Т та Ж) завжди лежать на одній лінії. Це легко доводиться методом подібності. Отримані трикутники БЕС та АЕД подібні, і в кожному з них медіани ЕТ та ЇЖ ділять кут при вершині Е на рівні частини. Отже точки Е, Т і Ж лежать на одній прямій. Так само на одній прямій розташовуються точки Т, О, і Ж. Все це випливає з подоби трикутників БОС та АОД. Звідси робимо висновок, що всі чотири точки – Е, Т, Про та Ж – лежатимуть на одній прямій.
Використовуючи такі трапеції, можна запропонувати учням знайти довжину відрізка (ЛФ), який розбиває фігуру на дві подібні. Даний відрізок повинен бути паралельний до основ. Оскільки отримані трапеції АЛФД і ЛБСФ подібні, БС/ЛФ=ЛФ/АД. Звідси випливає, що ЛФ=√(БС*АД). Отримуємо, що відрізок, що розбиває трапецію на дві подібні, має довжину, що дорівнює середньому геометричному довжини основ фігури.
Розглянемо наступна властивістьподоби. В його основі лежить відрізок, який поділяє трапецію на дві рівновеликі постаті. Вважаємо, що трапеція АБСД розділена відрізком ЄП на дві подібні. З вершини Б опущена висота, яка розбивається відрізком ЄП на дві частини – В1 та В2. Отримуємо: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 та ПАБСД = (БС+АД)*(В1+В2)/2. Далі складаємо систему, перше рівняння якої (БС+ЕН)*В1 = (АД+ЕН)*В2 та друге (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Звідси випливає, що В2/ В1 = (БС+ЕН)/(АД+ЕН) і БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Отримуємо, що довжина відрізка, що ділить трапецію на дві рівновеликі, дорівнює середньому квадратичному довжини основ: √((БС2+АД2)/2).
Висновки подібності
Таким чином, ми довели, що:
1. Відрізок, що з'єднує у трапеції середини бічних сторін, паралельний АТ і БС і дорівнює середньому арифметичному БС та АТ (довжина основи трапеції).
2. Риса, яка проходить через точку Про перетину діагоналей паралельно АТ і БС, дорівнюватиме середньому гармонійному чисел АТ і БС (2*БС*АД/(БС+АД)).
3. Відрізок, що розбиває трапецію на подібні, має довжину середньої геометричної основ БС та АТ.
4. Елемент, що ділить фігуру на дві рівновеликі, має довжину середнього квадратичного чисел АТ та БС.
Для закріплення матеріалу та усвідомлення зв'язку між розглянутими відрізками учню необхідно збудувати їх для конкретної трапеції. Він легко зможе відобразити середню лінію і відрізок, який проходить через точку О - перетин діагоналів фігури - паралельно підставам. А ось де будуть перебувати третій та четвертий? Ця відповідь приведе учня до відкриття шуканого зв'язку між середніми величинами.
Відрізок, що з'єднує середини діагоналей трапеції
Розглянемо таку властивість цієї фігури. Приймаємо, що відрізок МН паралельний основам і поділяє діагоналі навпіл. Точки перетину назвемо Ш і Щ. Даний відрізок дорівнюватиме напіврізності підстав. Розберемо це детальніше. МШ – середня лінія трикутника АБС, вона дорівнює БС/2. МЩ – середня лінія трикутника АБД, вона дорівнює АТ/2. Тоді отримуємо, що ШЩ = МЩ-МШ, отже, ШЩ = АТ/2-БС/2 = (АТ+ВС)/2.
Центр ваги
Давайте розглянемо, як визначається цей елемент для даної геометричної фігури. Для цього необхідно продовжити підстави протилежні сторони. Що це означає? Потрібно до верхньої основи додати нижнє - у будь-яку зі сторін, наприклад, праворуч. А нижнє подовжуємо на довжину верхнього вліво. Далі з'єднуємо їх діагоналлю. Точка перетину цього відрізка із середньою лінією фігури і є центром тяжкості трапеції.
Вписані та описані трапеції
Давайте перерахуємо особливості таких фігур:
1. Трапеція може бути вписана в коло тільки у тому випадку, якщо вона рівнобедрена.
2. Біля кола можна описати трапецію, за умови, що сума довжин їх підстав дорівнює сумі довжин бічних сторін.
Наслідки вписаного кола:
1. Висота описаної трапеції завжди дорівнює двом радіусам.
2. Бічна сторона описаної трапеції спостерігається із центру кола під прямим кутом.
Перше слідство очевидно, а для доказу другого потрібно встановити, що кут СОД є прямим, що, по суті, також не складе великих зусиль. Зате знання даної властивості дозволить при розв'язанні задач застосовувати прямокутний трикутник.
Тепер конкретизуємо ці наслідки для рівнобедреної трапеції, яка вписана в коло. Отримуємо, що висота є середнім геометричним підставам фігури: Н=2R=√(БС*АД). Відпрацьовуючи основний прийом розв'язання завдань для трапецій (принцип проведення двох висот), учень має вирішити таке завдання. Приймаємо, що БТ – висота рівнобедреної фігури АБСД. Необхідно знайти відрізки АТ та ТД. Застосовуючи формулу, описану вище, це зробити не складно.
Тепер давайте розберемося, як визначити радіус кола, використовуючи площу описаної трапеції. Опускаємо з вершини Б висоту на основу АТ. Оскільки коло вписано в трапецію, то БС+АД = 2АБ або АБ = (БС+АД)/2. З трикутника АБН знаходимо sinα = БН/АБ = 2*БН/(БС+АТ). ПАБСД = (БС + АТ) * БН / 2, БН = 2R. Отримуємо ПАБСД = (БС+АД)*R, звідси випливає, що R = ПАБСД/(БС+АД).
.
Усі формули середньої лінії трапеції
Тепер настав час перейти до останнього елемента даної геометричної фігури. Розберемося, чому дорівнює середня лінія трапеції (М):
1. Через підстави: М = (А + Б)/2.
2. Через висоту, основу та кути:
М = А-Н * (ctgα + ctgβ) / 2;
М = Б+Н*(ctgα+ctgβ)/2.
3. Через висоту, діагоналі та кут між ними. Наприклад, Д1 і Д2 - діагоналі трапеції; α , β - кути між ними:
М = Д1 * Д2 * sinα / 2Н = Д1 * Д2 * sinβ / 2Н.
4. Через площу та висоту: М = П/Н.
Перш ніж розбиратися, як знайти діагональ трапеції, пригадаємо, що таке трапеція. У планіметрії трапецією називають чотирикутник, у якого дві протилежні сторони паралельні одна одній. Ці паралельні сторони називають основами трапеції, інші - бічними сторонами. Бічні сторони можуть бути однаковими, тоді ми маємо справу з рівнобедреною трапецією.
Далі докладно розберемо порядок знаходження довжини діагоналей для загального випадку – нерівностегнової трапеції. При цьому виходитимемо з того, що вихідними даними є довжини всіх чотирьох сторін трапеції, кути біля основи невідомі.
Розрахунок діагоналі трапеції
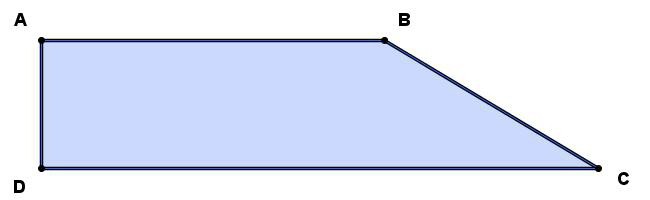
У зображеній малюнку трапеції ABCD є дві діагоналі AC і BD. Порядок знаходження їх довжини однаковий, тому розглянемо все на прикладі знаходження діагоналі BD, що протилежить BAD.
Діагональ BD одночасно є стороною трикутника ABD і може бути розрахована за теоремою косінусів за допомогою формули:
BD = √(AB 2 +AD 2 -2AB . AD . cos BAD)
У цій формулі нам відомі всі величини, крім косинуса BAD. Щоб визначити його, нам необхідно буде виконати невелике перетворення малюнка. "Виріжемо" з вихідної трапеції прямокутник BNMC. В результаті отримаємо трикутник ABD", в якому сторона BD" дорівнюватиме стороні трапеції CD.

˂BAD" у трикутнику дорівнює ˂BAD у трапеції, оскільки жодних перетворень з трикутником ABN ми не виконували. Отже, у цьому трикутнику ABD" сторона AB нам відома, сторона BD" = CD, а сторона AD" = AD – NM = AD - BC.
Виходить, що за теоремою косінусів cos BAD = cos BAD "= (AB 2 + AD" 2 - BD "2) / 2AB. AD" = (AB 2 + (AD - BC) 2 - CD 2) / 2AB . (AD – BC)
Підставивши тепер отриманий вираз у знайдену раніше формулу, отримаємо:
BD = √(AB 2 +AD 2 -2AB . AD . cos BAD) = √(AB 2 +AD 2 -2AB . AD . (AB 2 +(AD – BC) 2 – CD 2)/2AB . – BC)) = √(AB 2 + AD 2 – AD . (AB 2 +(AD – BC) 2 – CD 2)/(AD – BC)) = √(AB 2 + AD 2 – AD . (AD – BC) 2 /(AD – BC) – AD . )/(AD – BC)) = √(AB 2 + AD . BC – AD . (AB 2 – CD 2)/(AD – BC))
BD = √(AB 2 + AD . BC – AD . (AB 2 – CD 2)/(AD – BC))
Отримана формула діагоналі трапеції справедлива будь-яких значень довжин сторін вихідного чотирикутника.
Для другої діагоналі формула відповідно набуде вигляду:
AC = √(CD 2 + AD . BC – AD . (CD 2 – AB 2)/(AD – BC))
Діагональ рівнобедреної трапеції
Якщо вас цікавить, як знайти діагональ рівнобедреної трапеції, формулу, що вийшла, можна значно спростити. Адже в рівнобедреній трапеції AB = CD, отже AB 2 – CD 2 = 0 і формула довжини діагоналі наводиться до вигляду:
BD = √(AB 2 + AD . BC)
Діагоналі рівнобедреної трапеції дорівнюють один одному, тому друга діагональ знаходиться за тією самою формулою.
У тому випадку, якщо вихідними даними є довжини основ трапеції, одна з бічних сторін і кути при підставі, завдання знаходження діагоналі трапеції зводиться до розрахунку сторони трикутника по теоремі косінусів.
(від др.-грец. τραπέζιον - «столик»; τράπεζα - «стіл, їжа») - чотирикутник, у якого лише одна пара протилежних сторін паралельна.
Іноді трапеція визначається як чотирикутник, у якого пара протилежних сторін паралельна (про іншу не уточнюється), у цьому випадку є окремим випадком трапеції. Зокрема існує поняття криволінійна трапеція.
Елементи трапеції
- Паралельні сторониназиваються підставамитрапеції.
- Дві інші сторони називаються бічними сторонами.
- , що з'єднує середини бічних сторін, називається середньою лінієютрапеції.
- Відстань між основами називається заввишкитрапеції.
Види трапецій
- Трапеція, у якої бічні сторони рівні, називається рівнобедреної.
- Трапеція, у якої один із кутів "прямий", називається прямокутної.
Загальні властивості
- Середня лінія трапеції паралельна основам і дорівнює їх напівсумі.
- Відрізок, що з'єднує середини діагоналей, дорівнює напіврізниці основ.
- (Узагальнена Фалеса). Паралельні прямі сторони кута, що перетинають, відсікають від сторін кута пропорційні відрізки.
Властивості рівнобедреної трапеції
- , що проходить через середини основ, перпендикулярна до основ і є віссю симетрії трапеції.
- Висота, опущена з вершини на більшу основу, ділить його на два відрізки, один з яких дорівнює напівсумі основ, інший - напіврізниці основ.
- У рівнобедреній трапеції кути за будь-якої підстави рівні.
- У рівнобедреній трапеції довжини діагоналей рівні.
- Біля рівнобедреної трапеції можна описати.
- Якщо в рівнобедреній трапеції діагоналі перпендикулярні, то висота дорівнює напівсумі основ,
Чотирьохкутник, у якого тільки дві сторони паралельні називаються трапецією.
Паралельні сторони трапеції називаються її підставами, а ті сторони, які не паралельні, називаються бічними сторонами. Якщо бічні сторони рівні, така трапеція є рівнобедренной. Відстань між основами називається висотою трапеції.
Середня Лінія Трапеції
Середня лінія – це відрізок, що з'єднує середини бічних сторін трапеції. Середня лінія трапеції паралельна до її підстав.
Теорема:
Якщо пряма, що перетинає середину одного боку, паралельна підставам трапеції, вона ділить навпіл другу бічну сторонутрапеції.
Теорема:
Довжина середньої лінії дорівнює середньому арифметичному довжин її основ
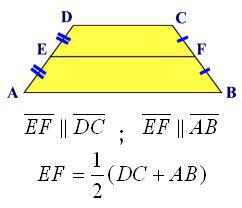
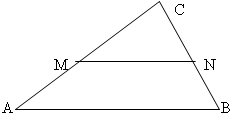
MN | AB || DCAM = MD; BN = NC
MN середня лінія, AB та CD - основи, AD та BC - бічні сторони
MN = (AB + DC)/2
Теорема:
Довжина середньої лінії трапеції дорівнює середньому арифметичному довжин її основ.
Основна задача: Довести, що середня лінія трапеції ділить навпіл відрізок, кінці якого лежать у середині основ трапеції
Середня лінія трикутника
Відрізок, що з'єднує середини двох сторін трикутника, називається середньою лінією трикутника. Вона паралельна третій стороні та її довжина дорівнює половині довжини третьої сторони.
Теорема: Якщо пряма, що перетинає середину однієї сторони трикутника, паралельна іншій стороні трикутника, то вона ділить третю сторону навпіл.
AM = MC та BN = NC =>
Застосування властивостей середньої лінії трикутника та трапеції
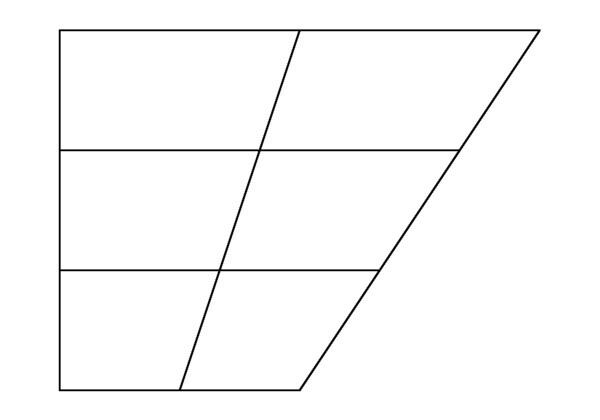
Розподіл відрізка на певну кількість рівних частин.
Завдання: Розділити відрізок AB на 5 рівних частин.
Рішення:
Нехай p це випадковий промінь, у якого почало це точка А, який не лежить на прямій AB. Ми послідовно відкладаємо 5 рівних сегментів на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Ми з'єднуємо A 5 з B і проводимо такі прямі через A 4 , A 3 , A 2 і A 1 , які є паралельними A 5 B. Вони перетинають AB відповідно в точках B 4 , B 3 , B 2 і B 1 . Ці точки поділяють відрізок AB на 5 рівних частин. Справді, з трапеції BB 3 A 3 A 5 бачимо, що BB 4 = B 4 B 3 . Таким же чином, з трапеції B 4 B 2 A 2 A 4 отримуємо B 4 B 3 = B 3 B 2
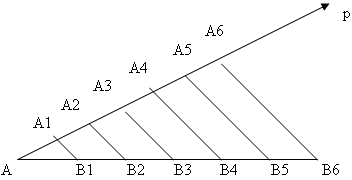
У той час як з трапеції B3B1A1A3, B3B2 = B2B1.
Тоді з B 2 AA 2 випливає, що B 2 B 1 = B 1 A. Наприкінці отримуємо:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, що для поділу відрізка AB на іншу кількість рівних частин, нам потрібно проектувати таку ж кількість рівних сегментів на промінь p. І далі продовжувати вищеописаним способом.



















