Property of a chord perpendicular to the diameter. Secant lines and chords in a circle. Average level. Properties of chords and tangents
A chord is a segment that connects two arbitrary points of one circle. Finding the length of a given element of a circle is a problem related to the geometric branch of mathematics. To calculate it, it is necessary to focus on the quantities given in the problem, as well as the properties of other elements.
There are several types of chord finding problems. Each of them contains different meanings, which can be used to carry out the necessary calculations.
The following diagrams show summary some chord theorems: perpendicular bisector and congruent chords. Scroll down the page for examples, explanations and solutions. A chord is a straight line connecting 2 points along the circumference of a circle.
Theorem. A radius or diameter perpendicular to a chord divides the chord into two equal parts and vice versa. Converse: the perpendicular bisector of a chord passes through the center of the circle. If two chords in a circle are congruent, then their intercepted arcs are congruent. Converse: if two arcs are congruent, then their corresponding chords are congruent.
How to find the chord of a circle - case 1
A circle is specified in which there is a radius R. If the arc φ is subtended by the chord L, and φ is specified in degrees, then the value of the chord length will be calculated as follows: L = 2*R*sin(φ/2). To solve the problem, you just need to substitute the numerical values and calculate.
How to find the chord of a circle - case 2
- A circle is specified, the center of which lies at point O and the chords AB and AC intersect the circle at the common point A. In this case, the angle formed by the chords (BAC) is based on the diameter. IN in this case It is recommended to make an explanatory drawing so that the formation of an isosceles triangle ABC can be seen, in which BC is the base and diameter, therefore BO=OC (as radii). Then AO is the median in the triangle and another radius. AB and AC are the sides of the triangle, AB = AC (since the triangle is isosceles). Triangles AOC and AOB are rectangular and isosceles. Knowing the radius, the chord is calculated using the Pythagorean theorem: AC 2 = AO 2 + OC 2.
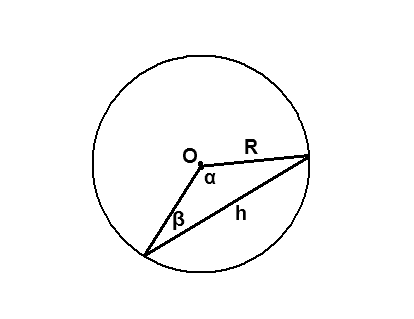
- In this case, you can use another formula if the diameter and the central angle on which the chord rests are known: L = 2R*Sin (α/2) = D*Sin (α/2).
Circle and circle. Basic concepts and properties
This video discusses the following theorems. Congruent central angles have congruent chords. Congruent chords have congruent arcs. Congruent arcs have congruent central angles. This video describes the four properties of chords. If two chords in a circle are congruent, then they define two central angles, which are congruent. If two chords in a circle are congruent, then their intercepted arcs are congruent. If two chords in a circle are congruent, then they are equidistant from the center of the circle.
How to find the chord of a circle - case 3
When a circle with a diameter and a chord is specified and the angle between them (α) is given, it is necessary to draw a perpendicular to the center from another point where the chord intersects the circle. You will get a right triangle. The projection theorem allows us to derive a formula that can be used to find the chord: CE = 2* R *cos α.
A perpendicular from the center of the circle to the chord bisects the chord. Try the examples provided or enter your own problem and check your answer with step-by-step explanations. Figure 1 Circle with four radii and two chords. Theorem 78: In a circle, if two chords are equal in measure, then the corresponding minor arcs are equal in measure.
The converse of this theorem is also true. Theorem 79: In a circle, if two measuring arcs are equal in measure, then their corresponding chords are equal in measure. Figure 2 Relationship between equality of measures of chords and equality of measures of their corresponding minor arcs.
How to find the chord of a circle - useful properties
- The chord passing through the center of a given circle will be its diameter.
- If there are two chords in a circle that intersect each other, then the following property works: the angle between them will be equal to ½ the sum of the measures of two arcs: the one located opposite the chord and the one located in the corner.
- In the case when a tangent is drawn to a given circle, which forms an angle with the chord, then it will be equal to the value obtained by dividing the value of the arc that the given chord subtends by 2.
Part 3. Circles
Below are some additional theorems about chords in a circle without explanation. These theorems can be used to solve many problems. Theorem 80: if the diameter is perpendicular to the chord, then it bisects the chord and its arcs. Figure 3 Diameter perpendicular to the chord.
Theorem 81: In a circle, if two chords are equal in measure, then they are equidistant from the center. Figure 4 In a circle, the relationship between two chords is uniform and equidistant from the center. Theorem 82: In a circle, if two chords are equidistant from the center of the circle, then the two chords are equal in measure.
I. Reference materials.
I. Properties of tangents, chords and secants. Inscribed and central angles.
Circle and Circle
1. If from one point lying outside the circle we draw two tangents to it, then
a) the lengths of the segments from a given point to the points of contact are equal;
b) the angles between each tangent and secant passing through the center of the circle are equal.
Figure 6 A circle with two minor arcs of equal measure. Figure 7 A circle with a diameter perpendicular to the chord. Given a point outside the circle, two lines can be drawn through this point that touch the circle. Tangent segments whose endpoints are points of tangency and a fixed point outside the circle are equal. In other words, tangent segments drawn to the same circle from the same point are equal.
Figure%: Tangent segments that divide an endpoint not in a circle are equal. Chords within a circle can be connected in many ways. Parallel chords in the same circle always cut congruent arcs. That is, arcs whose endpoints include one endpoint from each chord have equal measures.
2. If from one point lying outside the circle we draw a tangent and a secant to it, then the square of the tangent is equal to the product of the secant and its outer part
3. If two chords intersect at one point, then the product of segments of one chord is equal to the product of segments of the other.
4. Circumference C=2πR;
5. Arc length L =πRn/180˚
When congruent chords are in the same circle, they are equidistant from the center. Figure%: Congruent chords in the same circle are equidistant from the center. Last word on chords: chords of the same length in the same circle cut congruent arcs. That is, if the endpoints of one chord are the endpoints of one arc, then two arcs defined by two congruent chords in the same circle are congruent.
Intersection of chords, tangents and secants
A number of interesting theorems arise from the relationships between chords, secant segments, and tangent segments that intersect. First of all, we must define the secant segment. A second segment is a line segment with one end point around the circle, one end point outside the circle, and one point between those points that intersect the circle. There are three theorems regarding the above segments.
6. Area of a circle S=πR 2
7. Sector area S c=πR 2 n/360
The degree measure of an inscribed angle is equal to half the degree measure of the arc on which it rests.
Theorem 1. The measure of the angle between a tangent and a chord having a common point on a circle is equal to half the degree measure of the arc enclosed between its sides
Theorem 2(about tangent and secant). If a tangent and a secant are drawn from point M to a circle, then the square of the tangent segment from point M to the point of tangency is equal to the product of the lengths of the secant segments from point M to the points of its intersection with the circle.
Theorem 3. If two chords of a circle intersect, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord, that is, if the chords AB and CD intersect at point M, then AB MV = CM MD.
Properties of circle chords:
A diameter perpendicular to a chord divides it in half. Conversely: the diameter passing through the middle of the chord is perpendicular to it.
Equal chords of a circle are at equal distances from the center of the circle. Conversely: equal chords are located at equal distances from the center of the circle.
Arcs of a circle enclosed between parallel chords are equal.
circles that have a common point and a common tangent at this point are called tangent. If the circles are located on one side of the common tangent, then they are called internally tangent, and if on opposite sides of the tangent, then they are called externally tangent.
II. Additional materials
Properties of some angles.
Theorem.
1) An angle (ABC), the vertex of which lies inside the circle, is the half-sum of two arcs (AC and DE), one of which is between its sides, and the other between the extensions of the sides.
2) an angle (ABC), the vertex of which lies outside the circle and the sides intersect with the circle, is the half-difference of two arcs (AC and ED) enclosed between its sides
Proof .
Drawing the chord AD (on both drawings), we get ∆АВD,
relative to which the angle under consideration ABC serves as external when its vertex lies inside the circle, and internal when its vertex lies outside the circle. Therefore, in the first case: ; in the second case:
But angles ADC and DAE, like inscribed ones, are measured by half arcs AC and DE; therefore, angle ABC is measured: in the first case by the sum: ½ ﬞ AC+1/2 ﬞ DE, which is equal 1
/
2
(ﮟ
AC+ﮞ
DE), and in the second case, the difference is 1 / 2 ﬞ AC- 1 / 2 ﬞ DE, which is equal to 1 / 2 (ﬞ AC- ﬞ DE). Theorem. The angle (ACD) formed by a tangent and a chord is measured by half the arc contained within it. Now let's take the general case when the chord CD does not pass through the center. Drawing then the diameter CE, we will have: U Proportional lines in a circle Theorem. If some chord (AB) and a diameter (CD) are drawn through a point (M) taken inside a circle, then the product of chord segments (AM MB) is equal to the product of diameter segments (MB MC). Proof. P AM: MD=MS: MV, from where AM MV=MD MS. Consequence. If any number of chords (AB, EF, KL,...) are drawn through a point (M) taken inside a circle, then the product of segments of each chord is a constant number for all chords, since for each cord this product is equal to the product of segments of diameter CD passing through the taken point M. Theorem. If from a point (M) taken outside the circle, some secant (MA) and tangent (MS) are drawn to it, then the product of the secant and its outer part is equal to the square of the tangent (it is assumed that the secant is limited by the second point of intersection, and the tangent - point of contact). Let's draw auxiliary chords AC and BC; then we get two triangles MAC and MVS (covered in the figure with dashes), which are similar because they have a common angle M and angles MSV and CAB are equal, since each of them is measured by half of the arc BC. Let us take the MA and MC sides in ∆MAS; similar parties in ∆MVS will be MC and MV; therefore MA: MS = MS: MV, whence MA MV = MS 2. Consequence. If from a point (M) taken outside the circle, any number of secants (MA, MD, ME,...) are drawn to it, then the product of each secant and its external part is a constant number for all secants, since for each secant this the product is equal to the square of the tangent (MC 2) drawn from point M. III. Introductory tasks. Task 1. IN Solution 1) The radius of a circle circumscribed about a trapezoid is the same as the radius of a circle circumscribed about a triangle whose vertices are any three vertices of the trapezoid. Find the radius R of the circle circumscribed about the triangle ABD. 2)
ABCD is an isosceles trapezoid, therefore A.K. = M.D., K.M. =. In ∆ ABK A.K.
= AB cos A = · cos 60° = . Means, B.K. = AB sin A
=
· = . 3) By the cosine theorem in ∆ ABD
BD 2
= AB 2
+ AD 2
– 2AB ·
AD cos A. BD 2 = () 2 + (3) 2 – 2 3 = 21 + 9 21 – 3 21 = 7 21; 3) ∆CMN ∾
∆ CAB, which means ∆ CMN– equilateral C.M. = CN = MN = = 6; P. And 3) BN = C.B. – CN = 18 – 6 = 12. 4) P ( AMNB)
= A.M. + MN
+ BN + AB
= 18 + 6 + 12 + 12 = 48. An isosceles trapezoid is described around a circle, the middle line of which is equal to 5, and the sine of the acute angle at the base is equal to 0.8. Find the area of the trapezoid. Solution. FP– the middle line of the trapezoid, which means B.C. + AD = 2FP. Then AB = CD = FP = 5. ∆ABK– rectangular, B.K. = AB sin A; B.K.= 5 · 0.8 = 4. S ( ABCD)
= FP · B.K.= 5 · 4 = 20. Answer:
20. The incircle of triangle ABC touches side BC at point K, and the excircle touches side BC at point L. Prove that CK=BL=(a+b+c)/2 Proof: let M and N be the tangent points of the inscribed circle with sides AB and BC. Then BK+AN=BM+AM=AB, so CK+CN= a+b-c. Let P and Q be the points of tangency of the excircle with the extensions of the sides AB and BC. Then AP=AB+BP=AB+BL and AQ=AC+CQ=AC+CL. Therefore AP+AQ=a+b+c. Therefore, BL=BP=AP-AB=(a+b-c)/2. a) The continuation of the bisector of angle B of triangle ABC intersects the circumcircle at point M. O is the center of the inscribed circle. O B is the center of the excircle tangent to side AC. Prove that points A, C, O and O B lie on a circle with center M. D b) Point O, lying inside triangle ABC, has the property that straight lines AO, BO, CO pass through the centers of the circumscribed circles of triangles BCO, ACO, ABO. Prove that O is the center of the inscribed circle of triangle ABC IV. Additional tasks No. 1. The circle tangent to the hypotenuse of a right triangle and the extensions of its legs has radius R. Find the perimeter of the triangle R 1) ∆OAH =∆OAF along the leg and hypotenuse =>HA=FA 2) ∆OCF=∆OCG =>CF=CG 3) P ABC =AB+AF+FC+BC=AB+AM+GC+BC+BH+BG=2R No. 2. Points C and D lie on a circle with diameter AB. AC ∩ BD = P, and AD ∩ BC = Q. Prove that the lines AB and PQ are perpendicular Proof: A No. 3. In parallelogram ABCD, the diagonal AC is greater than the diagonal BD; M is a point on diagonal AC, BDCM is a cyclic quadrilateral. Prove that line BD is a common tangent to the circumcircles of triangles ABM and ADM P No. 4. N According to introductory problem 4 CM=(AC+CE-AE)/2 and CN=(BC+CE-BE)/2. Considering that AC=BC, we get MN=|CM-CN|=|AE-BE|/2 No. 5. The lengths of the sides of triangle ABC form an arithmetic progression, and a Let M be the midpoint of side AC, N the point of tangency of the inscribed circle with side BC. Then BN=р–b (introductory problem 4), therefore BN=AM, because p=3b/2 by condition. Besides, V
.Tasks for independent solution
No. 1. Quadrilateral ABCD has the property that there is a circle inscribed in angle BAD and tangent to the extensions of sides BC and CD. Prove that AB+BC=AD+DC. No. 2. The common internal tangent to circles with radii R and r intersects their common external tangents at points A and B and touches one of the circles at point C. Prove that AC∙CB=Rr No. 3. In triangle ABC, angle C is a right angle. Prove that r =(a+b-c)/2 and r c =(a+b+c)/2 No. 4. Two circles intersect at points A and B; MN is the common tangent to them. Prove that line AB divides segment MN in half. No. 5. Continuations of the bisectors of the angles of triangle ABC intersect the circumscribed circle at points A 1, B 1, C 1. M – point of intersection of bisectors. Prove that: a) MA·MC/MB 1 =2r; b) MA 1 ·MC 1 /MB=R No. 6. The angle formed by two tangents drawn from one point on a circle is equal to 23°15`. Calculate arcs between tangent points No. 7. Calculate the angle formed by the tangent and the chord if the chord divides the circle into two parts in a ratio of 3:7. VI. Control tasks. Option 1. Point M is located outside the circle with center O. Three secants are drawn from point M: the first intersects the circle at points B and A (M-B-A), the second at points D and C (M-D-C), and the third intersects the circle at points F and E (M-F-E) and passes through the center of the circle, AB = 4, BM =5, FM = 3. Prove that if AB = CD, then angles AME and CME are equal. Find the radius of the circle. Find the length of the tangent drawn from point M to the circle. Find angle AEB. Option 2. Prove that if AB = CD, then angles AME and CME are equal. AB is the diameter of a circle with center O. The chord EF intersects the diameter at point K (A-K-O), EK = 4, KF = 6, OK = 5. Find the distance from the center of the circle to the chord BF. Find the acute angle between the diameter AB and the chord EF. What is the chord FM equal to if EM is parallel to AB? Option 3. In right triangle ABC ( Option 4. AB is the diameter of a circle with center O. The radius of this circle is 4, O 1 is the middle of OA. A circle is drawn with the center at point O 1, tangent to the larger circle at point A. The chord CD of the larger circle is perpendicular to AB and intersects AB at point K. E and F are the points of intersection of CD with the smaller circle (C-E-K-F-D), AK=3. Find the chords AE and AC. Find the degree measure of arc AF and its length. Find the area of the part of the smaller circle cut off by the chord EF.
Let us first assume that the chord CD passes through the center O, i.e. that a chord is a diameter. Then the angle ACD-
straight and therefore equal to 90°. But half of the arc CmD is also equal to 90°, since the whole arc CmD, making up a semicircle, contains 180°. This means that the theorem is true in this particular case.
the goal ACE, as composed by the tangent and the diameter, is measured, as proven, by half the arc CDE; The angle DCE, as an inscribed one, is measured by half the arc CnED: the only difference in the proof is that this angle should not be considered as a difference, but as the sum of the right angle ALL and the acute angle ECD.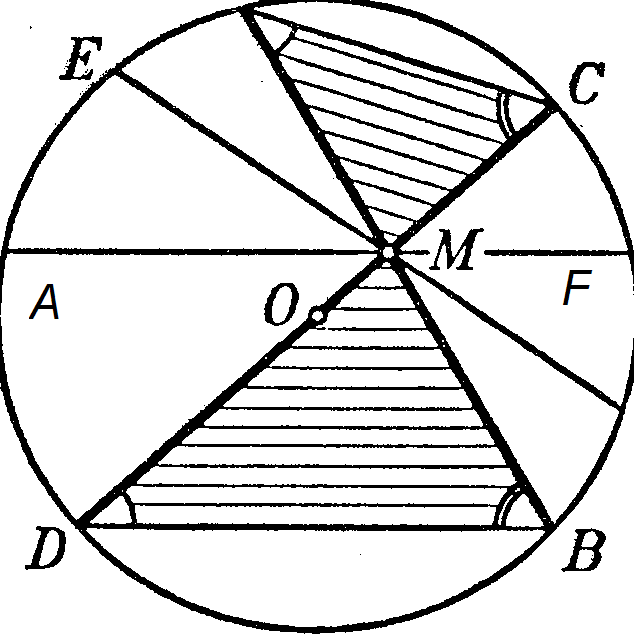
By drawing two auxiliary chords AC and BD, we get two triangles AMC and MBD (covered in the figure with dashes), which are similar, since their angles A and D are equal, like inscribed ones, based on the same arc BC, angles C and B are equal, as inscribed, based on the same arc AD. From the similarity of triangles we deduce:
Proof.
of an isosceles trapezoid with an acute angle of 60°, the lateral side is equal to , and the smaller base is equal to . Find the radius of the circle circumscribed by this trapezoid.
AD
=
.
BD= .CD = 3 · C.P..
Since a circle is inscribed in a quadrilateral, then B.C. + AD = AB + CD. This quadrilateral is an isosceles trapezoid, which means B.C. + AD = 2AB.
proof: Because
Proof: Let P be the circumcenter of triangle ACO. Then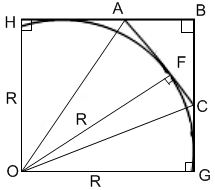
solution: HOGB - square with side R
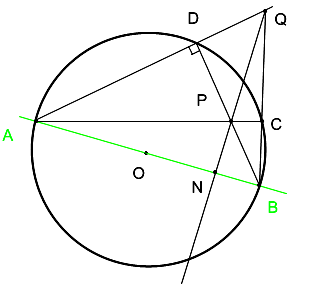D – diameter => inscribed angle ADB=90 o (as based on the diameter)=> QD/QP=QN/QA; ∆QDP is similar to ∆QNA on 2 sides and the angle between them => QN is perpendicular to AB.
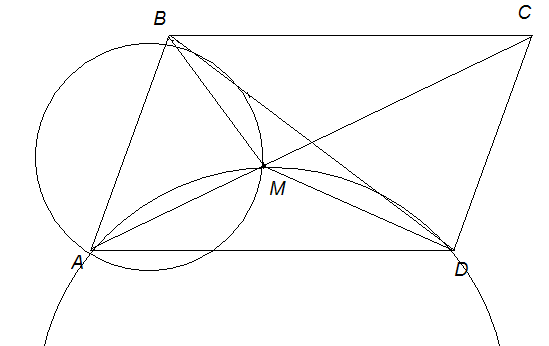mouth O is the point of intersection of diagonals AC and ВD. Then MO ·
OC=BO ·
OD. Whereas OS=OA and VO=ВD, then MO ·
OA=VO 2 and MO ·
OA=DO 2. These equalities mean that OB is tangent to the circumcircle of triangle ADM
At the base AB of the isosceles triangle ABC, point E is taken, and circles touching the segment CE at points M and N are inscribed in triangles ACE and ABE. Find the length of the segment MN if the lengths AE and BE are known.
Find the radius of the circle circumscribed by triangle ACE.
