The circumference is denoted by the letter C and is calculated by the formula:

C = 2πR,
Where R - circle radius.

Derivation of a formula expressing the circumference of a circle

Path C and C' are the lengths of circles of radii R and R'. Let us inscribe a regular n-gon in each of them and denote by P n and P" n their perimeters, and by a n and a" n their sides. Using the formula for calculating the side of a regular n-gon a n = 2R sin (180°/n) we get:
P n \u003d n a n \u003d n 2R sin (180 ° / n),
P "n \u003d n a" n \u003d n 2R "sin (180 ° / n).
Hence,
P n / P" n \u003d 2R / 2R". (1)
This equality is true for any value of n. We will now increase the number n indefinitely. Since P n → C, P" n → C", n → ∞, the limit of the relation P n / P" n is equal to C / C". On the other hand, due to equality (1), this limit is equal to 2R / 2R". Thus, C / C" = 2R / 2R". From this equality it follows that C / 2R = C" / 2R", i.e. . the ratio of a circle's circumference to its diameter is the same number for all circles. This number is usually denoted by the Greek letter π ("pi").
From the equality C / 2R = π we obtain a formula for calculating the circumference of a circle of radius R:
С = 2πR.

Let's first understand the difference between a circle and a circle. To see this difference, it is enough to consider what both figures are. This is an infinite number of points in the plane, located at an equal distance from a single central point. But, if the circle also consists of internal space, then it does not belong to the circle. It turns out that a circle is both a circle that bounds it (o-circle (g)ness), and an uncountable number of points that are inside the circle.

For any point L lying on the circle, the equality OL=R applies. (The length of the segment OL is equal to the radius of the circle).

A line segment that connects two points on a circle is chord.

A chord passing directly through the center of a circle is diameter this circle (D) . The diameter can be calculated using the formula: D=2R

Circumference calculated by the formula: C=2\pi R

Area of ​​a circle: S=\pi R^(2)

arc of a circle called that part of it, which is located between two of its points. These two points define two arcs of a circle. The chord CD subtends two arcs: CMD and CLD. The same chords subtend the same arcs.

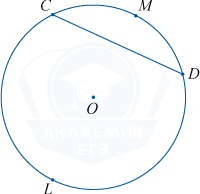
Central corner is the angle between two radii.

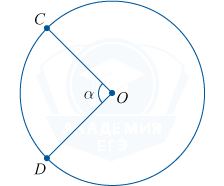
arc length can be found using the formula:

1. Using degrees: CD = \frac(\pi R \alpha ^(\circ))(180^(\circ))
2. Using a radian measure: CD = \alpha R

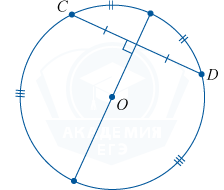
The diameter, which is perpendicular to the chord, bisects the chord and the arcs it spans.

If the chords AB and CD of the circle intersect at the point N, then the products of the segments of the chords separated by the point N are equal to each other.

AN\cdot NB = CN \cdot ND

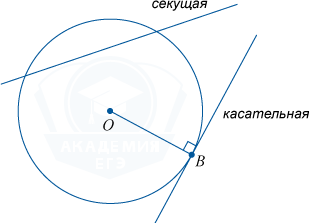
Tangent to circle

Tangent to a circle It is customary to call a straight line that has one common point with a circle.

If a line has two points in common, it is called secant.

If you draw a radius at the point of contact, it will be perpendicular to the tangent to the circle.

Let's draw two tangents from this point to our circle. It turns out that the segments of the tangents will be equal to one another, and the center of the circle will be located on the bisector of the angle with the vertex at this point.

AC=CB

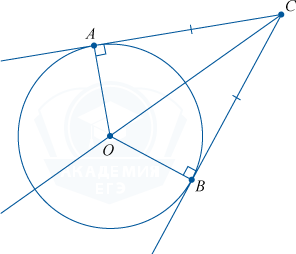
Now we draw a tangent and a secant to the circle from our point. We get that the square of the length of the tangent segment will be equal to the product of the entire secant segment by its outer part.

AC^(2) = CD \cdot BC

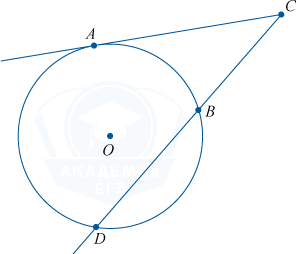
We can conclude: the product of an integer segment of the first secant by its outer part is equal to the product of an integer segment of the second secant by its outer part.

AC \cdot BC = EC \cdot DC

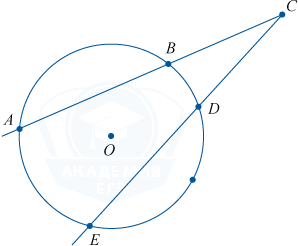
Angles in a circle

degree measures central corner and the arcs on which it rests are equal.

\angle COD = \cup CD = \alpha ^(\circ)

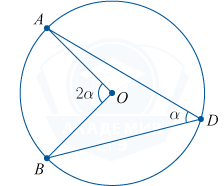
Inscribed angle is an angle whose vertex is on a circle and whose sides contain chords.

You can calculate it by knowing the size of the arc, since it is equal to half of this arc.

\angle AOB = 2 \angle ADB

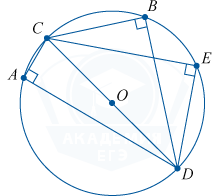
Based on a diameter, inscribed angle, straight.

\angle CBD = \angle CED = \angle CAD = 90^ (\circ)

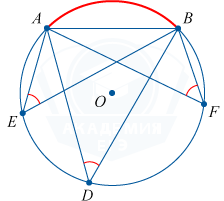
Inscribed angles that lean on the same arc are identical.

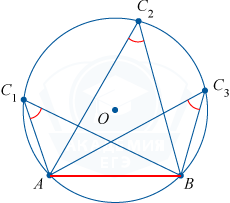
The inscribed angles based on the same chord are identical or their sum equals 180^ (\circ) .

\angle ADB + \angle AKB = 180^ (\circ)

\angle ADB = \angle AEB = \angle AFB

On the same circle are the vertices of triangles with identical angles and a given base.

An angle with a vertex inside the circle and located between two chords is identical to half the sum of the angular magnitudes of the arcs of the circle that are inside the given and vertical angles.

\angle DMC = \angle ADM + \angle DAM = \frac(1)(2) \left (\cup DmC + \cup AlB \right)

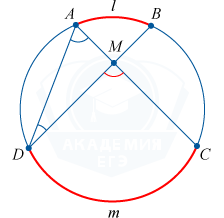
An angle with a vertex outside the circle and located between two secants is identical to half the difference in the angular magnitudes of the arcs of a circle that are inside the angle.

\angle M = \angle CBD - \angle ACB = \frac(1)(2) \left (\cup DmC + \cup AlB \right)

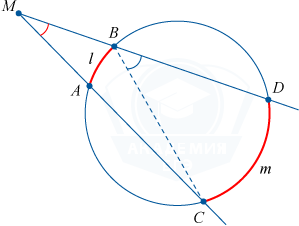
Inscribed circle

Inscribed circle is a circle tangent to the sides of the polygon.

At the point where the bisectors of the angles of the polygon intersect, its center is located.

A circle may not be inscribed in every polygon.

The area of ​​a polygon with an inscribed circle is found by the formula:

S=pr,

p is the semiperimeter of the polygon,

r is the radius of the inscribed circle.

It follows that the radius of the inscribed circle is:

r = \frac(S)(p)

Length sums opposite sides will be identical if the circle is inscribed in a convex quadrilateral. And vice versa: a circle is inscribed in a convex quadrilateral if the sums of the lengths of opposite sides in it are identical.

AB+DC=AD+BC

It is possible to inscribe a circle in any of the triangles. Only one single. At the point where the bisectors of the inner angles of the figure intersect, the center of this inscribed circle will lie.

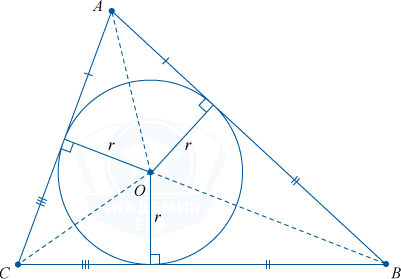
The radius of the inscribed circle is calculated by the formula:

r = \frac(S)(p) ,

where p = \frac(a + b + c)(2)

Circumscribed circle

If a circle passes through every vertex of a polygon, then such a circle is called circumscribed about a polygon.

The center of the circumscribed circle will be at the point of intersection of the perpendicular bisectors of the sides of this figure.

The radius can be found by calculating it as the radius of a circle that is circumscribed about a triangle defined by any 3 vertices of the polygon.

There is the following condition: a circle can be circumscribed around a quadrilateral only if the sum of its opposite angles is equal to 180^( \circ) .

\angle A + \angle C = \angle B + \angle D = 180^ (\circ)

Near any triangle it is possible to describe a circle, and one and only one. The center of such a circle will be located at the point where the perpendicular bisectors of the sides of the triangle intersect.

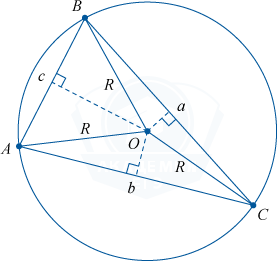
The radius of the circumscribed circle can be calculated by the formulas:

R = \frac(a)(2 \sin A) = \frac(b)(2 \sin B) = \frac(c)(2 \sin C)

R = \frac(abc)(4S)

a, b, c are the lengths of the sides of the triangle,

S is the area of ​​the triangle.

Ptolemy's theorem

Finally, consider Ptolemy's theorem.

Ptolemy's theorem states that the product of the diagonals is identical to the sum of the products of the opposite sides of an inscribed quadrilateral.

AC \cdot BD = AB \cdot CD + BC \cdot AD

In whatever area of ​​the economy a person works, wittingly or unwittingly, he uses the mathematical knowledge accumulated over many centuries. We encounter devices and mechanisms containing circles every day. A round shape has a wheel, pizza, many vegetables and fruits in the section form a circle, as well as plates, cups, and much more. However, not everyone knows how to correctly calculate the circumference.

To calculate the circumference of a circle, you must first remember what a circle is. This is the set of all points in the plane equidistant from the given one. A circle is a locus of points in a plane that is inside a circle. From the above, it follows that the perimeter of a circle and the circumference of a circle are one and the same.

Ways to find the circumference of a circle

In addition to the mathematical way of finding the perimeter of a circle, there are also practical ones.

• Take a rope or cord and wrap it around once.
• Then measure the rope, the resulting number will be the circumference.
• Roll a round object once and calculate the length of the path. If the object is very small, you can wrap it with twine several times, then unwind the thread, measure and divide by the number of turns.
• Find the required value using the formula:

L = 2πr = πD ,

where L is the desired length;

π is a constant, approximately equal to 3.14 r is the radius of the circle, the distance from its center to any point;

D is the diameter, it is equal to two radii.

Applying the formula to find the circumference of a circle

• Example 1. The treadmill runs around a circle with a radius of 47.8 meters. Find the length of this treadmill, assuming π = 3.14.

L \u003d 2πr \u003d 2 * 3.14 * 47.8 ≈ 300 (m)

Answer: 300 meters

• Example 2. A bicycle wheel, turning around 10 times, traveled 18.85 meters. Find the radius of the wheel.

18.85: 10 = 1.885 (m) is the perimeter of the wheel.

1.885: π \u003d 1.885: 3.1416 ≈ 0.6 (m) - the desired diameter

Answer: wheel diameter 0.6 meters

The amazing number π

Despite the apparent simplicity of the formula, for some reason it is difficult for many to remember it. Apparently, this is due to the fact that the formula contains an irrational number π, which is not present in the area formulas of other figures, for example, a square, a triangle or a rhombus. You just need to remember that this is a constant, that is, a constant, meaning the ratio of the circumference to the diameter. About 4 thousand years ago, people noticed that the ratio of the perimeter of a circle to its radius (or diameter) is the same for any circles.

The ancient Greeks approximated the number π with the fraction 22/7. For a long time, π was calculated as the average between the lengths of inscribed and circumscribed polygons in a circle. In the third century AD, a Chinese mathematician performed a calculation for a 3072-gon and obtained an approximate value of π = 3.1416. It must be remembered that π is always constant for any circle. Its designation with the Greek letter π appeared in the 18th century. This is the first letter Greek wordsπεριφέρεια - circumference and περίμετρος - perimeter. In the eighteenth century, it was proved that this quantity is irrational, that is, it cannot be represented as m/n, where m is an integer and n is a natural number.

In school mathematics, high accuracy of calculations is usually not needed, and π is taken equal to 3.14.

A circle is a closed curve, all points of which are at the same distance from the center. This figure is flat. Therefore, the solution to the problem, the question of which is how to find the circumference of a circle, is quite simple. All available methods, we will consider in today's article.

Figure descriptions

In addition to a fairly simple descriptive definition, there are three more mathematical characteristics of a circle, which in themselves contain the answer to the question of how to find the circumference of a circle:

• Consists of points A and B and all others from which AB can be seen at right angles. The diameter of this figure is equal to the length of the segment under consideration.
• Includes only points X such that the ratio AX/BX is constant and not equal to one. If this condition is not met, then it is not a circle.
• It consists of points, for each of which the following equality holds: the sum of the squared distances to the other two is a given value, which is always greater than half the length of the segment between them.

Terminology

Not everyone at school had a good math teacher. Therefore, the answer to the question of how to find the circumference of a circle is also complicated by the fact that not everyone knows the basic geometric concepts. Radius is a segment that connects the center of the figure with a point on the curve. A special case in trigonometry is the unit circle. A chord is a line segment that connects two points on a curve. For example, the already considered AB falls under this definition. Diameter is a chord passing through the center. The number π is equal to the length of the unit semicircle.

Basic Formulas

Geometric formulas directly follow from the definitions, which allow you to calculate the main characteristics of the circle:

1. The length is equal to the product of the number π and the diameter. The formula is usually written as follows: C = π*D.
2. The radius is half the diameter. It can also be calculated by calculating the quotient of dividing the circumference by twice the number π. The formula looks like this: R = C/(2* π) = D/2.
3. The diameter is equal to the circumference divided by π or twice the radius. The formula is quite simple and looks like this: D = C/π = 2*R.
4. The area of ​​a circle is equal to the product of the number π and the square of the radius. Similarly, diameter can be used in this formula. In this case, the area will be equal to the quotient of dividing the product of the number π and the square of the diameter by four. The formula can be written as follows: S = π*R 2 = π*D 2 /4.

How to find the circumference of a circle from a diameter

For simplicity of explanation, we denote by letters the characteristics of the figure necessary for calculating. Let C be the desired length, D be its diameter, and let pi be approximately 3.14. If we have only one known quantity, then the problem can be considered solved. Why is it necessary in life? Suppose we decide to enclose a round pool with a fence. How to calculate the required number of columns? And here the ability to calculate the circumference of a circle comes to the rescue. The formula is as follows: C = π D. In our example, the diameter is determined based on the radius of the pool and the required distance to the fence. For example, suppose that our home artificial reservoir is 20 meters wide, and we are going to put posts at a distance of ten meters from it. The diameter of the resulting circle is 20 + 10 * 2 = 40 m. Length - 3.14 * 40 = 125.6 meters. We will need 25 columns if the gap between them is about 5 m.

Length through radius

As always, let's start by assigning letter circles to characteristics. In fact, they are universal, so mathematicians from different countries it is not necessary to know each other's language. Suppose C is the circumference of a circle, r is its radius, and π is approximately 3.14. The formula looks like this in this case: C = 2*π*r. Obviously, this is an absolutely correct equality. As we have already figured out, the diameter of a circle is equal to twice its radius, so this formula looks like this. In life, this method can also often come in handy. For example, we bake a cake in a special sliding form. So that it does not get dirty, we need a decorative wrapper. But how to cut a circle of the desired size. This is where mathematics comes to the rescue. Those who know how to find out the circumference of a circle will immediately say that you need to multiply the number π by twice the radius of the shape. If its radius is 25 cm, then the length will be 157 centimeters.

Task examples

We have already considered several practical cases of the acquired knowledge on how to find out the circumference of a circle. But often we are not concerned with them, but with the real mathematical problems that are contained in the textbook. After all, the teacher gives points for them! Therefore, let's consider a problem of increased complexity. Let's assume that the circumference is 26 cm. How to find the radius of such a figure?

Example Solution

To begin with, let's write down what is given to us: C \u003d 26 cm, π \u003d 3.14. Also remember the formula: C = 2* π*R. From it you can extract the radius of the circle. Thus, R= C/2/π. Now let's proceed to the direct calculation. First, divide the length by two. We get 13. Now we need to divide by the value of the number π: 13 / 3.14 \u003d 4.14 cm. It is important not to forget to write down the answer correctly, that is, with units of measurement, otherwise the whole practical meaning of such problems is lost. In addition, for such inattention, you can get a score of one point lower. And no matter how annoying it may be, you have to put up with this state of affairs.

The beast is not as scary as it is painted

So we figured out such a difficult task at first glance. As it turned out, you just need to understand the meaning of the terms and remember a few easy formulas. Math is not so scary, you just need to make a little effort. So geometry is waiting for you!