वृत्त की परिधि को अक्षर द्वारा दर्शाया जाता है सीऔर सूत्र द्वारा गणना की जाती है:

सी = 2πआर,
कहाँ आर - वृत्त की त्रिज्या.

परिधि को व्यक्त करने वाले सूत्र की व्युत्पत्ति

पथ C और C' त्रिज्या R और R' वाले वृत्तों की लंबाई हैं। आइए उनमें से प्रत्येक में एक नियमित एन-गॉन अंकित करें और उनकी परिधि को पी एन और पी" एन से और उनकी भुजाओं को ए एन और ए" एन से निरूपित करें। नियमित एन-गॉन ए एन = 2आर पाप (180 डिग्री/एन) के पक्ष की गणना के लिए सूत्र का उपयोग करके हम प्राप्त करते हैं:
पी एन = एन ए एन = एन 2आर पाप (180°/एन),
पी" एन = एन · ए" एन = एन · 2आर" पाप (180°/एन)।
इस तरह,
पी एन / पी" एन = 2आर / 2आर"। (1)
यह समानता n के किसी भी मान के लिए मान्य है। अब हम संख्या n को बिना किसी सीमा के बढ़ाएंगे। चूँकि P n → C, P" n → C", n → ∞, तो अनुपात P n / P" n की सीमा C / C" के बराबर है। दूसरी ओर, समानता (1) के आधार पर, यह सीमा 2R/2R के बराबर है। इस प्रकार, C/C" = 2R/2R"। इस समानता से यह निष्कर्ष निकलता है कि C/2R = C"/2R" , अर्थात। । किसी वृत्त की परिधि और उसके व्यास का अनुपात सभी वृत्तों के लिए समान संख्या है।यह संख्या आमतौर पर ग्रीक अक्षर π ("pi") द्वारा इंगित की जाती है।
समानता C / 2R = π से हमें त्रिज्या R वाले एक वृत्त की परिधि की गणना के लिए सूत्र प्राप्त होता है:
С = 2πR.

सबसे पहले, आइए वृत्त और वृत्त के बीच के अंतर को समझें। इस अंतर को देखने के लिए, यह विचार करना पर्याप्त है कि दोनों आंकड़े क्या हैं। ये समतल पर अनंत संख्या में बिंदु हैं, जो एक ही केंद्रीय बिंदु से समान दूरी पर स्थित हैं। लेकिन, यदि वृत्त में आंतरिक स्थान भी शामिल है, तो यह वृत्त से संबंधित नहीं है। यह पता चलता है कि एक वृत्त एक वृत्त है जो इसे सीमित करता है (सर्कल (आर)), और असंख्य बिंदु जो सर्कल के अंदर हैं।

वृत्त पर स्थित किसी भी बिंदु L के लिए, समानता OL=R लागू होती है। (खंड OL की लंबाई वृत्त की त्रिज्या के बराबर है)।

एक वृत्त पर दो बिंदुओं को जोड़ने वाला खंड उसका है तार.

वृत्त के केंद्र से सीधे गुजरने वाली एक जीवा है व्यासयह वृत्त (D). व्यास की गणना सूत्र का उपयोग करके की जा सकती है: D=2R

परिधिसूत्र द्वारा गणना: C=2\pi R

एक वृत्त का क्षेत्रफल: S=\pi R^(2)

एक वृत्त का चापइसका वह भाग कहलाता है जो इसके दो बिंदुओं के बीच स्थित होता है। ये दो बिंदु एक वृत्त के दो चापों को परिभाषित करते हैं। कॉर्ड सीडी दो चापों को अंतरित करती है: सीएमडी और सीएलडी। समान जीवाएँ समान चाप अंतरित करती हैं।

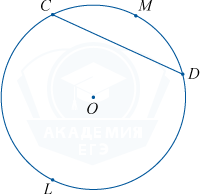
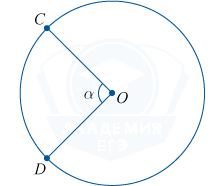
केन्द्रीय कोणवह कोण जो दो त्रिज्याओं के बीच स्थित होता है, कहलाता है।

वक्राकार लंबाईसूत्र का उपयोग करके पाया जा सकता है:

1. डिग्री माप का उपयोग करना: सीडी = \frac(\pi R \alpha ^(\circ))(180^(\circ))
2. रेडियन माप का उपयोग करना: CD = \alpha R

व्यास, जो जीवा के लंबवत है, जीवा और उसके द्वारा अनुबंधित चाप को आधे में विभाजित करता है।

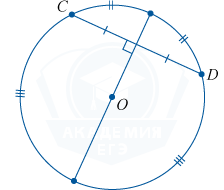
यदि किसी वृत्त की जीवाएँ AB और CD बिंदु N पर प्रतिच्छेद करती हैं, तो बिंदु N से अलग किए गए जीवाओं के खंडों का गुणनफल एक दूसरे के बराबर होता है।

एएन\सीडॉट एनबी = सीएन\सीडॉट एनडी

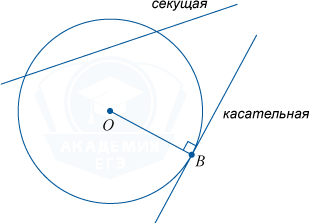
एक वृत्त की स्पर्शरेखा

एक वृत्त की स्पर्शरेखायह एक सीधी रेखा को कॉल करने की प्रथा है जिसमें एक वृत्त के साथ एक सामान्य बिंदु होता है।

यदि किसी रेखा में दो उभयनिष्ठ बिंदु हों तो उसे कहते हैं काटनेवाला.

यदि आप त्रिज्या को स्पर्शरेखा बिंदु पर खींचते हैं, तो यह वृत्त की स्पर्शरेखा के लंबवत होगी।

आइए इस बिंदु से हमारे वृत्त पर दो स्पर्शरेखाएँ खींचें। यह पता चला है कि स्पर्शरेखा खंड एक दूसरे के बराबर होंगे, और वृत्त का केंद्र इस बिंदु पर शीर्ष के साथ कोण के समद्विभाजक पर स्थित होगा।

एसी = सीबी

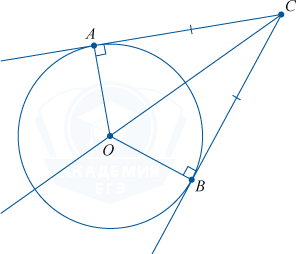
आइए अब अपने बिंदु से वृत्त पर एक स्पर्शरेखा और एक छेदक रेखा बनाएं। हम पाते हैं कि स्पर्श रेखा खंड की लंबाई का वर्ग संपूर्ण छेदक खंड और उसके बाहरी भाग के गुणनफल के बराबर होगा।

AC^(2) = CD \cdot BC

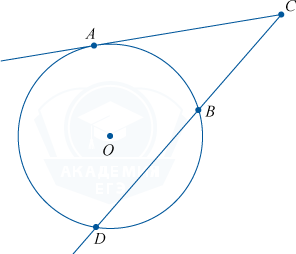
हम यह निष्कर्ष निकाल सकते हैं: पहले छेदक के एक पूरे खंड और उसके बाहरी भाग का उत्पाद दूसरे छेदक के एक पूरे खंड और उसके बाहरी हिस्से के उत्पाद के बराबर है।

AC\cdot BC = EC\cdot DC

एक वृत्त में कोण

डिग्री उपाय केंद्रीय कोणऔर जिस चाप पर यह टिका है वह बराबर है।

\कोण सीओडी = \कप सीडी = \अल्फा ^(\सर्कल)

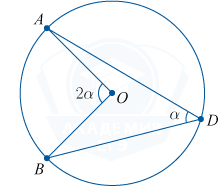
अंकित कोणवह कोण है जिसका शीर्ष एक वृत्त पर है और जिसकी भुजाओं में जीवाएँ हैं।

आप चाप का आकार जानकर इसकी गणना कर सकते हैं, क्योंकि यह इस चाप के आधे के बराबर है।

\कोण AOB = 2 \कोण ADB

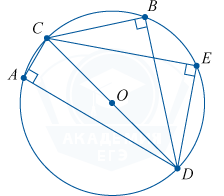
व्यास, अंकित कोण, समकोण के आधार पर।

\कोण CBD = \कोण CED = \कोण CAD = 90^ (\circ)

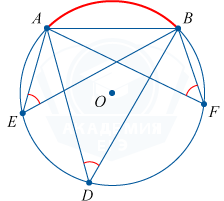
समान चाप को अंतरित करने वाले अंकित कोण समान होते हैं।

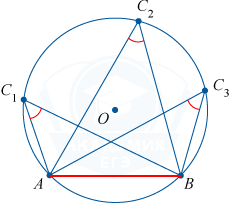
एक जीवा पर बने अंकित कोण समरूप होते हैं या उनका योग 180^ (\circ) के बराबर होता है।

\कोण ADB + \कोण AKB = 180^ (\circ)

\कोण एडीबी = \कोण एईबी = \कोण एएफबी

एक ही वृत्त पर समान कोण और दिए गए आधार वाले त्रिभुजों के शीर्ष हैं।

वृत्त के अंदर एक शीर्ष वाला और दो जीवाओं के बीच स्थित एक कोण, वृत्त के चापों के कोणीय मानों के आधे योग के समान होता है जो दिए गए और ऊर्ध्वाधर कोणों के भीतर समाहित होते हैं।

\कोण डीएमसी = \कोण एडीएम + \कोण डीएएम = \frac(1)(2) \बाएं (\कप डीएमसी + \कप अलबी \दाएं)

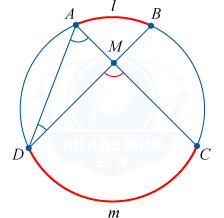
वृत्त के बाहर एक शीर्ष वाला और दो छेदक रेखाओं के बीच स्थित कोण, वृत्त के चापों के कोणीय मानों के आधे अंतर के समान होता है जो कोण के अंदर समाहित होते हैं।

\कोण एम = \कोण सीबीडी - \कोण एसीबी = \frac(1)(2) \बाएं (\कप डीएमसी + \कप अलबी \दाएं)

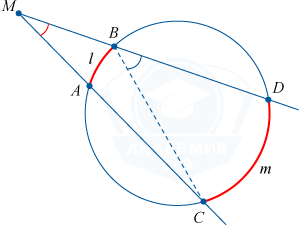
अंकित वृत्त

अंकित वृत्तबहुभुज की भुजाओं पर स्पर्शरेखा वाला एक वृत्त है।

उस बिंदु पर जहां बहुभुज के कोनों के समद्विभाजक प्रतिच्छेद करते हैं, उसका केंद्र स्थित होता है।

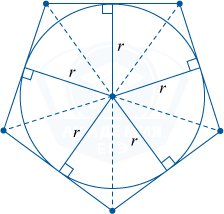
प्रत्येक बहुभुज में एक वृत्त अंकित नहीं किया जा सकता।

एक खुदे हुए वृत्त वाले बहुभुज का क्षेत्रफल सूत्र द्वारा ज्ञात किया जाता है:

एस = पीआर,

p बहुभुज का अर्ध-परिधि है,

r अंकित वृत्त की त्रिज्या है।

इससे यह निष्कर्ष निकलता है कि अंकित वृत्त की त्रिज्या बराबर है:

आर = \frac(एस)(पी)

लंबाई का योग विपरीत दिशाएंयदि वृत्त उत्तल चतुर्भुज में अंकित हो तो समरूप होगा। और इसके विपरीत: एक वृत्त एक उत्तल चतुर्भुज में फिट बैठता है यदि विपरीत भुजाओं की लंबाई का योग समान हो।

एबी + डीसी = एडी + बीसी

किसी भी त्रिभुज में एक वृत्त अंकित करना संभव है। केवल एक ही एक. उस बिंदु पर जहां आकृति के आंतरिक कोणों के समद्विभाजक प्रतिच्छेद करते हैं, इस उत्कीर्ण वृत्त का केंद्र स्थित होगा।

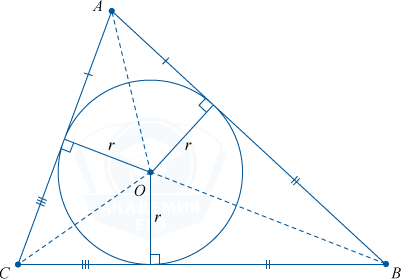
अंकित वृत्त की त्रिज्या की गणना सूत्र द्वारा की जाती है:

r = \frac(S)(p) ,

जहाँ p = \frac(a + b + c)(2)

परिवृत्त

यदि किसी बहुभुज के प्रत्येक शीर्ष से एक वृत्त गुजरता है, तो ऐसे वृत्त को आमतौर पर वृत्त कहा जाता है बहुभुज के बारे में बताया गया है.

इस आकृति की भुजाओं के लंब समद्विभाजक के प्रतिच्छेदन बिंदु पर परिवृत्त का केंद्र होगा।

त्रिज्या को उस वृत्त की त्रिज्या के रूप में गणना करके पाया जा सकता है जो बहुभुज के किन्हीं तीन शीर्षों द्वारा परिभाषित त्रिभुज के चारों ओर परिचालित है।

निम्नलिखित शर्त है: एक चतुर्भुज के चारों ओर एक वृत्त का वर्णन केवल तभी किया जा सकता है जब इसके सम्मुख कोणों का योग 180^( \circ) के बराबर हो।

\कोण A + \कोण C = \कोण B + \कोण D = 180^ (\circ)

किसी भी त्रिभुज के चारों ओर आप एक वृत्त का वर्णन कर सकते हैं, और केवल एक। ऐसे वृत्त का केंद्र उस बिंदु पर स्थित होगा जहां त्रिभुज की भुजाओं के लंबवत समद्विभाजक प्रतिच्छेद करते हैं।

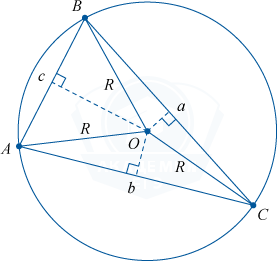
परिचालित वृत्त की त्रिज्या की गणना सूत्रों का उपयोग करके की जा सकती है:

आर = \frac(a)(2 \sin A) = \frac(b)(2 \sin B) = \frac(c)(2 \sin C)

आर = \frac(एबीसी)(4 एस)

a, b, c त्रिभुज की भुजाओं की लंबाई हैं,

S त्रिभुज का क्षेत्रफल है.

टॉलेमी का प्रमेय

अंत में, टॉलेमी के प्रमेय पर विचार करें।

टॉलेमी के प्रमेय में कहा गया है कि विकर्णों का उत्पाद चक्रीय चतुर्भुज के विपरीत पक्षों के उत्पादों के योग के समान है।

AC \cdot BD = AB \cdot CD + BC \cdot AD

इससे कोई फर्क नहीं पड़ता कि कोई व्यक्ति अर्थव्यवस्था के किस क्षेत्र में काम करता है, जाने-अनजाने वह कई शताब्दियों से संचित गणितीय ज्ञान का उपयोग करता है। हम हर दिन मंडल वाले उपकरणों और तंत्रों का सामना करते हैं। एक पहिये का आकार गोल होता है, पिज्जा, कई सब्जियां और फल काटने पर एक चक्र बनाते हैं, साथ ही प्लेट, कप और भी बहुत कुछ। हालाँकि, हर कोई नहीं जानता कि परिधि की सही गणना कैसे करें।

किसी वृत्त की परिधि की गणना करने के लिए, आपको पहले यह याद रखना होगा कि वृत्त क्या है। यह इससे समान दूरी पर स्थित समतल के सभी बिंदुओं का समुच्चय है। और एक वृत्त एक वृत्त के अंदर स्थित समतल पर बिंदुओं का एक ज्यामितीय स्थान है। उपरोक्त से यह निष्कर्ष निकलता है कि वृत्त की परिधि और परिधि एक ही हैं।

वृत्त की परिधि ज्ञात करने की विधियाँ

किसी वृत्त की परिधि ज्ञात करने की गणितीय विधि के अलावा, व्यावहारिक विधियाँ भी हैं।

• एक रस्सी या डोरी लें और उसे एक बार चारों ओर लपेट लें।
• फिर रस्सी को मापें, परिणामी संख्या परिधि होगी।
• गोल वस्तु को एक बार घुमाएँ और पथ की लंबाई गिनें। यदि वस्तु बहुत छोटी है, तो आप इसे कई बार सुतली से लपेट सकते हैं, फिर धागे को खोल सकते हैं, माप सकते हैं और घुमावों की संख्या से विभाजित कर सकते हैं।
• सूत्र का उपयोग करके आवश्यक मान ज्ञात करें:

एल = 2πआर = πडी ,

जहाँ L आवश्यक लंबाई है;

π एक स्थिरांक है, लगभग 3.14 r के बराबर वृत्त की त्रिज्या है, इसके केंद्र से किसी बिंदु तक की दूरी;

D व्यास है, यह दो त्रिज्याओं के बराबर है।

वृत्त की परिधि ज्ञात करने के लिए सूत्र का प्रयोग करना

• उदाहरण 1: एक ट्रेडमिल 47.8 मीटर की त्रिज्या वाले एक वृत्त के चारों ओर चलती है। π = 3.14 लेते हुए, इस ट्रेडमिल की लंबाई ज्ञात कीजिए।

एल = 2πr =2*3.14*47.8 ≈ 300(एम)

उत्तर: 300 मीटर

• उदाहरण 2. एक साइकिल का पहिया 10 बार घूमकर 18.85 मीटर चला है। पहिये की त्रिज्या ज्ञात कीजिए।

18.85:10 =1.885 (एम) पहिये का परिमाप है।

1.885: π = 1.885: 3.1416 ≈ 0.6 (एम) - आवश्यक व्यास

उत्तर: पहिये का व्यास 0.6 मीटर

अद्भुत संख्या पाई

सूत्र की स्पष्ट सरलता के बावजूद, किसी कारण से कई लोगों के लिए इसे याद रखना कठिन है। जाहिरा तौर पर, यह इस तथ्य के कारण है कि सूत्र में एक अपरिमेय संख्या π है, जो अन्य आंकड़ों के क्षेत्र के सूत्रों में मौजूद नहीं है, उदाहरण के लिए, एक वर्ग, त्रिकोण या समचतुर्भुज। आपको बस यह याद रखने की आवश्यकता है कि यह एक स्थिरांक है, अर्थात एक स्थिरांक जिसका अर्थ है परिधि और व्यास का अनुपात। लगभग 4 हजार साल पहले, लोगों ने देखा कि एक वृत्त की परिधि और उसकी त्रिज्या (या व्यास) का अनुपात सभी वृत्तों के लिए समान होता है।

प्राचीन यूनानियों ने भिन्न 22/7 के साथ संख्या π का ​​अनुमान लगाया था। लंबे समय तक, π की गणना एक वृत्त में अंकित और परिबद्ध बहुभुजों की लंबाई के बीच के औसत के रूप में की जाती थी। तीसरी शताब्दी ईस्वी में, एक चीनी गणितज्ञ ने 3072-गॉन के लिए गणना की और π = 3.1416 का अनुमानित मूल्य प्राप्त किया। यह याद रखना चाहिए कि किसी भी वृत्त के लिए π सदैव स्थिर रहता है। ग्रीक अक्षर π के साथ इसका पदनाम 18वीं शताब्दी में सामने आया। यह पहला अक्षर है ग्रीक शब्दπεριφέρεια - वृत्त और περίμετρος - परिधि। अठारहवीं शताब्दी में, यह सिद्ध हो गया कि यह मात्रा अपरिमेय है, अर्थात इसे m/n के रूप में प्रदर्शित नहीं किया जा सकता है, जहाँ m एक पूर्णांक है और n एक प्राकृतिक संख्या है।

स्कूली गणित में, आमतौर पर गणनाओं की उच्च सटीकता की आवश्यकता नहीं होती है, और π को 3.14 के बराबर लिया जाता है।

वृत्त एक बंद वक्र है जिसके सभी बिंदु केंद्र से समान दूरी पर होते हैं। यह आंकड़ा सपाट है. इसलिए, समस्या का समाधान, जिसका प्रश्न यह है कि परिधि कैसे ज्ञात करें, काफी सरल है। हम आज के लेख में सभी उपलब्ध तरीकों पर गौर करेंगे।

आकृति का विवरण

काफी सरल वर्णनात्मक परिभाषा के अलावा, एक वृत्त की तीन और गणितीय विशेषताएँ हैं, जिनमें स्वयं इस प्रश्न का उत्तर है कि परिधि कैसे ज्ञात करें:

• इसमें बिंदु A और B और अन्य सभी बिंदु शामिल हैं जिनसे AB को समकोण पर देखा जा सकता है। इस आकृति का व्यास विचाराधीन खंड की लंबाई के बराबर है।
• केवल वे बिंदु X शामिल हैं, जिनका अनुपात AX/BX स्थिर है और एक के बराबर नहीं है। यदि यह शर्त पूरी नहीं होती तो यह वृत्त नहीं है।
• इसमें बिंदु होते हैं, जिनमें से प्रत्येक के लिए निम्नलिखित समानता होती है: अन्य दो की दूरी के वर्गों का योग एक दिया गया मान होता है, जो हमेशा उनके बीच के खंड की लंबाई के आधे से अधिक होता है।

शब्दावली

स्कूल में हर किसी के पास गणित का अच्छा शिक्षक नहीं था। इसलिए, परिधि कैसे ज्ञात करें, इस प्रश्न का उत्तर इस तथ्य से और अधिक जटिल है कि हर कोई बुनियादी ज्यामितीय अवधारणाओं को नहीं जानता है। त्रिज्या एक खंड है जो किसी आकृति के केंद्र को वक्र पर एक बिंदु से जोड़ता है। त्रिकोणमिति में एक विशेष मामला इकाई वृत्त है। कॉर्ड एक खंड है जो वक्र पर दो बिंदुओं को जोड़ता है। उदाहरण के लिए, पहले से ही चर्चा की गई एबी इस परिभाषा के अंतर्गत आती है। व्यास केंद्र से गुजरने वाली जीवा है। संख्या π एक इकाई अर्धवृत्त की लंबाई के बराबर है।

मूल सूत्र

परिभाषाएँ सीधे ज्यामितीय सूत्रों का पालन करती हैं जो आपको एक वृत्त की मुख्य विशेषताओं की गणना करने की अनुमति देती हैं:

1. लंबाई संख्या π और व्यास के गुणनफल के बराबर है। सूत्र आमतौर पर इस प्रकार लिखा जाता है: C = π*D.
2. त्रिज्या आधे व्यास के बराबर है। इसकी गणना परिधि को संख्या π के दोगुने से विभाजित करने के भागफल की गणना करके भी की जा सकती है। सूत्र इस प्रकार दिखता है: R = C/(2* π) = D/2.
3. व्यास परिधि के भागफल को π या त्रिज्या के दोगुने से विभाजित करने के बराबर है। सूत्र काफी सरल है और इस तरह दिखता है: D = C/π = 2*R.
4. एक वृत्त का क्षेत्रफल π और त्रिज्या के वर्ग के गुणनफल के बराबर होता है। इसी प्रकार, इस सूत्र में व्यास का उपयोग किया जा सकता है। इस स्थिति में, क्षेत्रफल संख्या π और व्यास के वर्ग के गुणनफल के भागफल के बराबर होगा। सूत्र इस प्रकार लिखा जा सकता है: S = π*R 2 = π*D 2 /4.

व्यास द्वारा वृत्त की परिधि कैसे ज्ञात करें

स्पष्टीकरण की सरलता के लिए, आइए हम गणना के लिए आवश्यक आकृति की विशेषताओं को अक्षरों द्वारा निरूपित करें। मान लीजिए C वांछित लंबाई है, D इसका व्यास है, और π लगभग 3.14 के बराबर है। यदि हमारे पास केवल एक ज्ञात मात्रा है, तो समस्या का समाधान माना जा सकता है। जीवन में यह क्यों आवश्यक है? मान लीजिए कि हम एक गोल पूल को बाड़ से घेरने का निर्णय लेते हैं। कॉलमों की आवश्यक संख्या की गणना कैसे करें? और यहां परिधि की गणना करने की क्षमता बचाव में आती है। सूत्र इस प्रकार है: C = π D. हमारे उदाहरण में, व्यास पूल की त्रिज्या और बाड़ से आवश्यक दूरी के आधार पर निर्धारित किया जाता है। उदाहरण के लिए, मान लीजिए कि हमारे घर का कृत्रिम तालाब 20 मीटर चौड़ा है, और हम उससे दस मीटर की दूरी पर खंभे लगाने जा रहे हैं। परिणामी वृत्त का व्यास 20 + 10*2 = 40 मीटर है। लंबाई 3.14*40 = 125.6 मीटर है। यदि उनके बीच का अंतर लगभग 5 मीटर है तो हमें 25 खंभों की आवश्यकता होगी।

त्रिज्या के माध्यम से लंबाई

हमेशा की तरह, आइए वृत्त की विशेषताओं के लिए अक्षर निर्दिष्ट करके शुरुआत करें। वास्तव में, वे सार्वभौमिक हैं, इसलिए गणितज्ञों से विभिन्न देशएक-दूसरे की भाषा जानना बिल्कुल भी जरूरी नहीं है। आइए मान लें कि C वृत्त की परिधि है, r इसकी त्रिज्या है, और π लगभग 3.14 के बराबर है। इस मामले में सूत्र इस तरह दिखता है: C = 2*π*r. जाहिर है, यह बिल्कुल सही समीकरण है. जैसा कि हम पहले ही पता लगा चुके हैं, एक वृत्त का व्यास उसकी त्रिज्या के दोगुने के बराबर होता है, इसलिए यह सूत्र इस तरह दिखता है। जीवन में यह तरीका अक्सर काम भी आ सकता है। उदाहरण के लिए, हम एक केक को एक विशेष स्लाइडिंग रूप में बेक करते हैं। इसे गंदा होने से बचाने के लिए हमें एक सजावटी आवरण की आवश्यकता होती है। लेकिन आवश्यक आकार का गोला कैसे काटें। यहीं पर गणित बचाव में आता है। जो लोग किसी वृत्त की परिधि का पता लगाना जानते हैं, वे तुरंत कहेंगे कि आपको संख्या π को आकृति की त्रिज्या के दोगुने से गुणा करना होगा। यदि इसकी त्रिज्या 25 सेमी है तो लंबाई 157 सेमी होगी।

समस्याओं के उदाहरण

हम पहले ही किसी वृत्त की परिधि ज्ञात करने के बारे में प्राप्त ज्ञान के कई व्यावहारिक मामलों को देख चुके हैं। लेकिन अक्सर हम उनके बारे में नहीं, बल्कि पाठ्यपुस्तक में मौजूद वास्तविक गणितीय समस्याओं के बारे में चिंतित होते हैं। आख़िरकार, शिक्षक उनके लिए अंक देता है! तो आइए एक अधिक जटिल समस्या पर नजर डालें। आइए मान लें कि वृत्त की परिधि 26 सेमी है। ऐसी आकृति की त्रिज्या कैसे ज्ञात करें?

उदाहरण समाधान

सबसे पहले, आइए लिखें कि हमें क्या दिया गया है: C = 26 सेमी, π = 3.14। सूत्र भी याद रखें: C = 2* π*R. इससे आप वृत्त की त्रिज्या निकाल सकते हैं। इस प्रकार, आर= सी/2/π। अब आइए वास्तविक गणना पर आगे बढ़ें। सबसे पहले, लंबाई को दो से विभाजित करें। हमें 13 मिलता है। अब हमें संख्या π के मान से विभाजित करने की आवश्यकता है: 13/3.14 = 4.14 सेमी। यह महत्वपूर्ण है कि उत्तर को सही ढंग से लिखना न भूलें, यानी माप की इकाइयों के साथ, अन्यथा संपूर्ण व्यावहारिक अर्थ ऐसी समस्याएं खो जाती हैं। इसके अलावा, ऐसी असावधानी के लिए आपको एक अंक कम ग्रेड प्राप्त हो सकता है। और चाहे यह कितना भी कष्टप्रद क्यों न हो, आपको इस स्थिति से जूझना ही होगा।

यह जानवर उतना डरावना नहीं है जितना इसे चित्रित किया गया है

तो हमने पहली नज़र में ही इतना कठिन काम निपटा लिया है। जैसा कि यह पता चला है, आपको बस शब्दों के अर्थ को समझने और कुछ सरल सूत्रों को याद रखने की आवश्यकता है। गणित इतना डरावना नहीं है, आपको बस थोड़ा प्रयास करने की आवश्यकता है। तो ज्यामिति आपका इंतजार कर रही है!