पाठ विषय

• समांतर चतुर्भुज के विकर्णों के गुण.

पाठ मकसद

• नई परिभाषाओं से परिचित हों और पहले से पढ़ी गई कुछ परिभाषाओं को याद रखें।
• समांतर चतुर्भुज के विकर्णों का गुण बताएं और सिद्ध करें।
• समस्याओं को हल करते समय आकृतियों के गुणों को लागू करना सीखें।
• विकासात्मक - छात्रों का ध्यान, दृढ़ता, दृढ़ता, तार्किक सोच, गणितीय भाषण विकसित करना।
• शैक्षिक - पाठ के माध्यम से, एक-दूसरे के प्रति चौकस रवैया अपनाएं, साथियों को सुनने की क्षमता, पारस्परिक सहायता और स्वतंत्रता पैदा करें।

पाठ मकसद

• छात्रों की समस्या-समाधान कौशल का परीक्षण करें।

शिक्षण योजना

1. परिचय।
2. पहले अध्ययन की गई सामग्री की पुनरावृत्ति।
3. समांतर चतुर्भुज, इसके गुण और विशेषताएं।
4. कार्यों के उदाहरण.
5. अपने चेक।

परिचय

"एक प्रमुख वैज्ञानिक खोज एक बड़ी समस्या का समाधान प्रदान करती है, लेकिन किसी भी समस्या के समाधान में खोज का एक अंश होता है।"

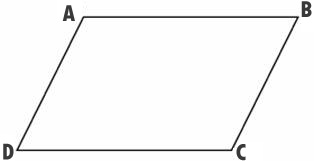
समांतर चतुर्भुज की विपरीत भुजाओं का गुण

एक समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।

सबूत।

माना ABCD दिया गया समांतर चतुर्भुज है। और मान लीजिए कि इसके विकर्ण बिंदु O पर प्रतिच्छेद करते हैं।
चूँकि त्रिभुजों की समानता के पहले मानदंड के अनुसार Δ AOB = Δ COD (∠ AOB = ∠ COD, ऊर्ध्वाधर के रूप में, AO=OC, DO=OB, समांतर चतुर्भुज के विकर्णों के गुण के अनुसार), तो AB=CD। इसी प्रकार, त्रिभुज BOC और DOA की समानता से यह निष्कर्ष निकलता है कि BC = DA. प्रमेय सिद्ध है.

समांतर चतुर्भुज के सम्मुख कोणों का गुण

समांतर चतुर्भुज में सम्मुख कोण बराबर होते हैं।

सबूत।

माना ABCD दिया गया समांतर चतुर्भुज है। और मान लीजिए कि इसके विकर्ण बिंदु O पर प्रतिच्छेद करते हैं।
एक समांतर चतुर्भुज की विपरीत भुजाओं के गुणों के बारे में प्रमेय में जो सिद्ध किया गया था, उससे तीन पक्षों पर Δ ABC = Δ CDA (AB=CD, BC=DA जो सिद्ध किया गया था, उससे AC - सामान्य)। त्रिभुजों की समानता से यह निष्कर्ष निकलता है कि ∠ ABC = ∠ CDA.
यह भी सिद्ध है कि ∠ DAB = ∠ BCD, जो ∠ ABD = ∠ CDB से अनुसरण करता है। प्रमेय सिद्ध है.

समांतर चतुर्भुज के विकर्णों की संपत्ति

समांतर चतुर्भुज के विकर्ण प्रतिच्छेद करते हैं और प्रतिच्छेदन बिंदु पर द्विभाजित होते हैं।

सबूत।

माना ABCD दिया गया समांतर चतुर्भुज है। आइए विकर्ण AC बनाएं। आइए इस पर मध्य O को चिह्नित करें। खंड DO की निरंतरता पर, हम खंड OB 1 को DO के बराबर अलग रख देंगे।
पिछले प्रमेय के अनुसार, AB 1 CD एक समांतर चतुर्भुज है। इसलिए, रेखा AB 1 DC के समानांतर है। लेकिन बिंदु A से होकर DC के समानांतर केवल एक रेखा खींची जा सकती है। इसका मतलब यह है कि रेखा AB 1, रेखा AB से संपाती है।
यह भी सिद्ध है कि BC 1 BC से मेल खाता है। इसका मतलब है कि बिंदु C, C 1 से मेल खाता है। समांतर चतुर्भुज ABCD समांतर चतुर्भुज AB 1 CD से मेल खाता है। परिणामस्वरूप, समांतर चतुर्भुज के विकर्ण प्रतिच्छेद करते हैं और प्रतिच्छेदन बिंदु पर द्विभाजित होते हैं। प्रमेय सिद्ध है.

के लिए पाठ्यपुस्तकों में नियमित विद्यालय(उदाहरण के लिए, पोगोरेलोव में) इसे इस प्रकार सिद्ध किया गया है: विकर्ण समांतर चतुर्भुज को 4 त्रिभुजों में विभाजित करते हैं। आइए एक जोड़ी को देखें और पता लगाएं - वे बराबर हैं: उनके आधार हैं - विपरीत दिशाएं, इसके निकटवर्ती संगत कोण समानांतर रेखाओं के ऊर्ध्वाधर कोणों के बराबर होते हैं। अर्थात्, विकर्ण खंड जोड़े में बराबर होते हैं। सभी।

बस इतना ही?
यह ऊपर सिद्ध किया गया था कि प्रतिच्छेदन बिंदु विकर्णों को समद्विभाजित करता है - यदि यह मौजूद है। उपरोक्त तर्क किसी भी तरह से इसके अस्तित्व को सिद्ध नहीं करता है। अर्थात्, प्रमेय का भाग "एक समांतर चतुर्भुज के विकर्ण प्रतिच्छेद करते हैं" अप्रमाणित रहता है।

मजेदार बात यह है कि इस हिस्से को साबित करना बहुत कठिन है। वैसे, यह एक अधिक सामान्य परिणाम से होता है: किसी भी उत्तल चतुर्भुज के विकर्ण प्रतिच्छेद नहीं करेंगे, लेकिन किसी भी गैर-उत्तल चतुर्भुज में ऐसा नहीं होगा।

एक भुजा और दो आसन्न कोणों के अनुदिश त्रिभुजों की समानता पर (त्रिभुजों की समानता का दूसरा चिह्न) और अन्य।

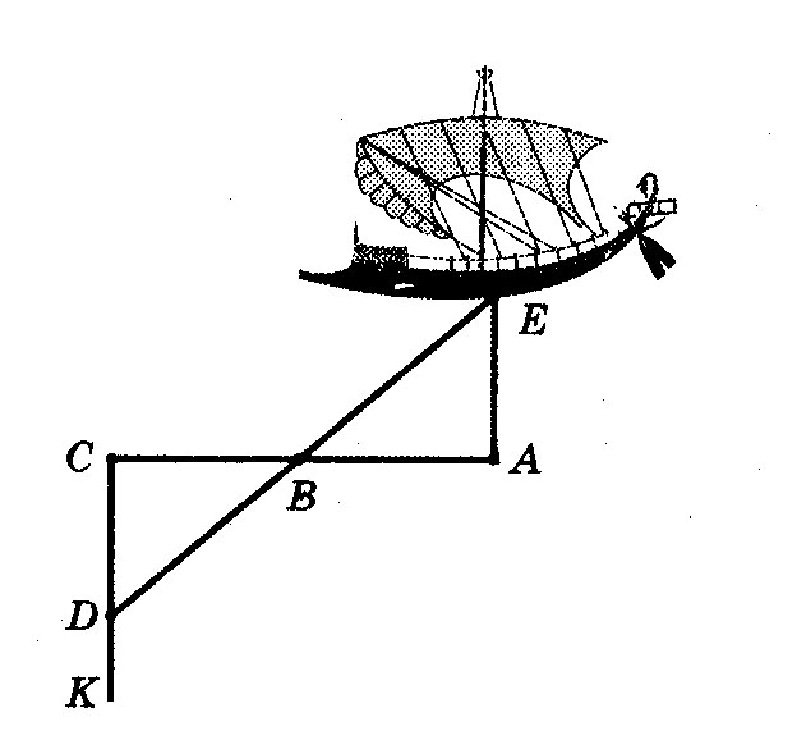
थेल्स ने एक भुजा पर बने दो त्रिभुजों और दो आसन्न कोणों की समानता पर एक महत्वपूर्ण प्रमेय पाया प्रायोगिक उपयोग. समुद्र में एक जहाज की दूरी निर्धारित करने के लिए मिलेटस के बंदरगाह में एक रेंजफाइंडर बनाया गया था। इसमें तीन संचालित खूंटियां ए, बी और सी (एबी = बीसी) और सीए के लंबवत एक चिह्नित सीधी रेखा एससी शामिल थी। जब एक जहाज एसके सीधी रेखा पर दिखाई दिया, तो हमें बिंदु डी इस प्रकार मिला कि बिंदु डी, .बी और ई एक ही सीधी रेखा पर थे। जैसा कि चित्र से स्पष्ट है, जमीन पर दूरी सीडी जहाज से वांछित दूरी है।

प्रशन

1. क्या किसी वर्ग के विकर्ण प्रतिच्छेदन बिंदु से आधे में विभाजित होते हैं?
   
2. क्या समांतर चतुर्भुज के विकर्ण बराबर होते हैं?
3. क्या समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं?
4. समांतर चतुर्भुज की परिभाषा बताएं?
5. एक समांतर चतुर्भुज के कितने चिन्ह होते हैं?
   
6. क्या एक समचतुर्भुज एक समांतर चतुर्भुज हो सकता है?
   

प्रयुक्त स्रोतों की सूची

1. कुज़नेत्सोव ए.वी., गणित शिक्षक (ग्रेड 5-9), कीव
2. "अकेला राज्य परीक्षा 2006. गणित. छात्रों को तैयार करने के लिए शैक्षिक और प्रशिक्षण सामग्री / रोसोब्रनाडज़ोर, आईएसओपी - एम.: इंटेलेक्ट-सेंटर, 2006"
3. मजूर के.आई. "एम.आई. स्कानवी द्वारा संपादित संग्रह के गणित में मुख्य प्रतिस्पर्धात्मक समस्याओं का समाधान"
4. एल. एस. अतानास्यान, वी. एफ. बुटुज़ोव, एस. बी. कदोमत्सेव, ई. जी. पॉज़्न्याक, आई. आई. युदिना "ज्यामिति, 7 - 9: शैक्षणिक संस्थानों के लिए पाठ्यपुस्तक"

हमने पाठ पर काम किया

कुज़नेत्सोव ए.वी.

पोटर्नक एस.ए.

एवगेनी पेत्रोव

आप आधुनिक शिक्षा के बारे में कोई प्रश्न उठा सकते हैं, कोई विचार व्यक्त कर सकते हैं या किसी गंभीर समस्या का समाधान कर सकते हैं शैक्षिक मंच, जहां नई सोच और कार्रवाई की एक शैक्षिक परिषद अंतरराष्ट्रीय स्तर पर मिलती है। बनाया है ब्लॉग,आप न केवल एक सक्षम शिक्षक के रूप में अपनी स्थिति में सुधार करेंगे, बल्कि भविष्य के स्कूल के विकास में भी महत्वपूर्ण योगदान देंगे। शैक्षिक नेताओं का गिल्डशीर्ष-रैंकिंग विशेषज्ञों के लिए दरवाजे खोलता है और उन्हें दुनिया में सर्वश्रेष्ठ स्कूल बनाने में सहयोग करने के लिए आमंत्रित करता है।

एक चतुर्भुज जिसकी सम्मुख भुजाएँ समान्तर हों, एक समांतर चतुर्भुज होता है। विकर्ण विपरीत शीर्षों को जोड़ने वाली सीधी रेखाएँ हैं। उनके प्रतिच्छेदन का बिंदु समरूपता का केंद्र है। सामान्य तौर पर, एक समांतर चतुर्भुज में दो विकर्ण होते हैं, D लंबा है और d छोटा है।

कोसाइन प्रमेय का उपयोग करके समांतर चतुर्भुज का विकर्ण ज्ञात करें

• समांतर चतुर्भुज कोण α और β की कोज्या का मान।

D = √a^2 + b^2 — 2ab cosβ

d = √a^2 + b^2 + 2ab cosβ

डी = √a^2 + b^2 + 2ab cosα

d = √a^2 + b^2 — 2ab cosα

एक ज्ञात विकर्ण और भुजाओं का उपयोग करके समांतर चतुर्भुज का विकर्ण ज्ञात करें

इस विधि का उपयोग करने के लिए आपको यह जानना आवश्यक है:

• समांतर चतुर्भुज a और b की भुजाओं की लंबाई।

डी = √2a^2 + 2b^2 — d^2

इस विधि का उपयोग करने के लिए आपको यह जानना आवश्यक है:

• समांतर चतुर्भुज का क्षेत्रफल.
• विकर्ण D या d में से किसी एक की लंबाई।
• विकर्णों γ या δ के बीच का कोण.

डी = 2एस/डी पापγ = 2एस/डी पापδ

डी = 2एस/डी सिनγ = 2एस/डी सिनδ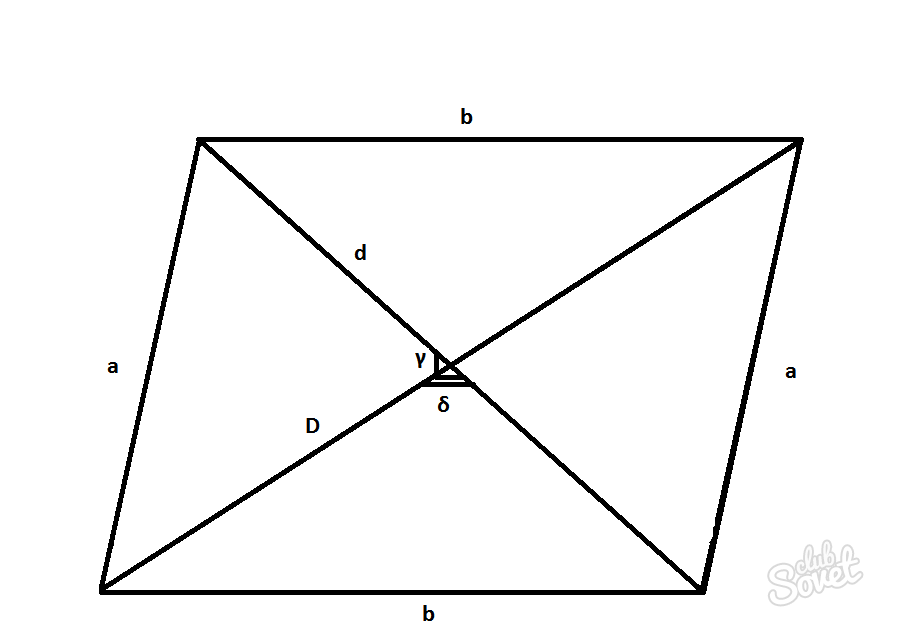

समांतर चतुर्भुज के विकर्ण की लंबाई निर्धारित करने का एक विशेष मामला एक वर्ग है

वर्ग एक समांतर चतुर्भुज है जिसकी सभी भुजाएँ बराबर होती हैं और कोण 90° होते हैं। इस मामले में विकर्णों की लंबाई D=d के बराबर होगी और पाइथागोरस प्रमेय का उपयोग करके गणना की जा सकती है।
D=d=a*√2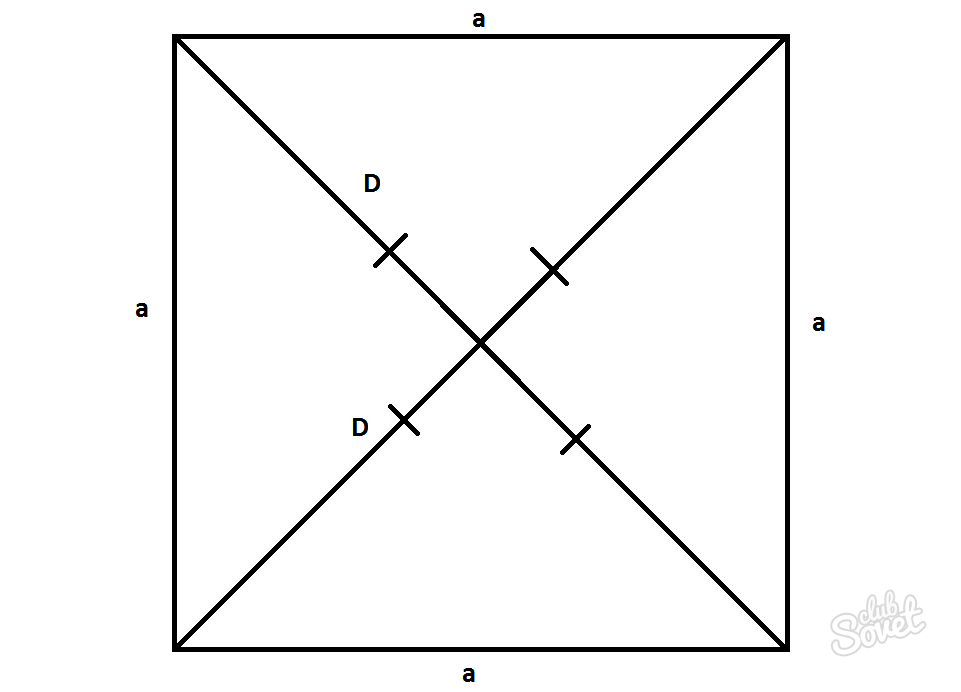

समांतर चतुर्भुज के विकर्ण की लंबाई निर्धारित करने का एक विशेष मामला एक आयत है

आयत एक समांतर चतुर्भुज है जिसके कोण बराबर और 90° के बराबर होते हैं। इस मामले में विकर्णों की लंबाई D=d के बराबर होगी और पाइथागोरस प्रमेय का उपयोग करके गणना की जा सकती है।
D=d=√(a^2+b^2)

समांतर चतुर्भुज एक चतुर्भुज है जिसकी सम्मुख भुजाएँ जोड़े में समांतर होती हैं। यह परिभाषा पहले से ही पर्याप्त है, क्योंकि समांतर चतुर्भुज के शेष गुण इसी से अनुसरण करते हैं और प्रमेयों के रूप में सिद्ध होते हैं।

समांतर चतुर्भुज के मुख्य गुण हैं:

• एक समांतर चतुर्भुज एक उत्तल चतुर्भुज है;
• एक समांतर चतुर्भुज की विपरीत भुजाएँ जोड़े में बराबर होती हैं;
• एक समांतर चतुर्भुज में, सम्मुख कोण जोड़े में बराबर होते हैं;
• समांतर चतुर्भुज के विकर्णों को प्रतिच्छेदन बिंदु द्वारा आधे में विभाजित किया जाता है।

समांतर चतुर्भुज - उत्तल चतुर्भुज

आइए पहले हम इस प्रमेय को सिद्ध करें समांतर चतुर्भुज एक उत्तल चतुर्भुज है. एक बहुभुज उत्तल होता है यदि इसकी किसी भी भुजा को एक सीधी रेखा तक बढ़ाया जाए, तो बहुभुज की अन्य सभी भुजाएँ इस सीधी रेखा के एक ही तरफ होंगी।

मान लीजिए कि एक समांतर चतुर्भुज ABCD दिया गया है, जिसमें AB, CD के लिए विपरीत भुजा है, और BC, AD के लिए विपरीत भुजा है। फिर समांतर चतुर्भुज की परिभाषा से यह निष्कर्ष निकलता है कि AB || सीडी, बीसी || ईसा पश्चात

समानांतर खंडों में कोई उभयनिष्ठ बिंदु नहीं होता और वे प्रतिच्छेद नहीं करते। इसका मतलब है कि CD, AB के एक तरफ स्थित है। चूँकि खंड BC खंड AB के बिंदु B को खंड CD के बिंदु C से जोड़ता है, और खंड AD अन्य बिंदुओं AB और CD को जोड़ता है, खंड BC और AD भी रेखा AB के उसी तरफ स्थित हैं जहाँ CD स्थित है। इस प्रकार, तीनों भुजाएँ - CD, BC, AD - AB के एक ही तरफ स्थित हैं।

इसी प्रकार, यह सिद्ध है कि समांतर चतुर्भुज की अन्य भुजाओं के संबंध में, अन्य तीन भुजाएँ एक ही तरफ स्थित होती हैं।

सम्मुख भुजाएँ और कोण बराबर होते हैं

समांतर चतुर्भुज का एक गुण यह है एक समांतर चतुर्भुज में सम्मुख भुजाएँ और सम्मुख कोण जोड़े में बराबर होते हैं. उदाहरण के लिए, यदि एक समांतर चतुर्भुज ABCD दिया गया है, तो इसमें AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D है। यह प्रमेय इस प्रकार सिद्ध होता है।

समांतर चतुर्भुज एक चतुर्भुज है। इसका मतलब है कि इसके दो विकर्ण हैं। चूँकि एक समांतर चतुर्भुज एक उत्तल चतुर्भुज है, उनमें से कोई भी इसे दो त्रिभुजों में विभाजित करता है। समांतर चतुर्भुज ABCD में, विकर्ण AC खींचकर प्राप्त त्रिभुज ABC और ADC पर विचार करें।

इन त्रिभुजों में एक भुजा उभयनिष्ठ है - AC। कोण बीसीए कोण के बराबरसीएडी समानांतर बीसी और एडी के साथ ऊर्ध्वाधर के रूप में। जब AB और CD समानांतर हों तो कोण BAC और ACD भी ऊर्ध्वाधर कोणों के बराबर होते हैं। इसलिए, दो कोणों और उनके बीच की भुजा पर ∆ABC = ∆ADC है।

इन त्रिभुजों में, भुजा AB, भुजा CD से मेल खाती है, और भुजा BC, AD से मेल खाती है। इसलिए, एबी = सीडी और बीसी = एडी।

कोण B, कोण D से मेल खाता है, अर्थात ∠B = ∠D. समांतर चतुर्भुज का कोण A दो कोणों - ∠BAC और ∠CAD का योग है। कोण C, ∠BCA और ∠ACD के बराबर है। चूँकि कोणों के जोड़े एक दूसरे के बराबर हैं, तो ∠A = ∠C.

इस प्रकार, यह सिद्ध है कि एक समांतर चतुर्भुज में सम्मुख भुजाएँ और कोण बराबर होते हैं।

विकर्णों को आधे में विभाजित किया गया है

चूँकि एक समांतर चतुर्भुज एक उत्तल चतुर्भुज है, इसमें दो विकर्ण होते हैं, और वे प्रतिच्छेद करते हैं। मान लीजिए समांतर चतुर्भुज ABCD दिया गया है, इसके विकर्ण AC और BD बिंदु E पर प्रतिच्छेद करते हैं। उनसे बने त्रिभुज ABE और CDE पर विचार करें।

इन त्रिभुजों की भुजाएँ AB और CD एक समांतर चतुर्भुज की विपरीत भुजाओं के बराबर हैं। कोण ABE, कोण CDE के बराबर है क्योंकि यह समानांतर रेखाओं AB और CD के साथ स्थित है। इसी कारण से, ∠BAE = ∠DCE. इसका मतलब है कि दो कोणों पर ∆ABE = ∆CDE और उनके बीच की भुजा।

आप यह भी देख सकते हैं कि कोण AEB और CED ऊर्ध्वाधर हैं और इसलिए एक दूसरे के बराबर भी हैं।

चूँकि त्रिभुज ABE और CDE एक दूसरे के बराबर हैं, तो उनके सभी संगत तत्व भी बराबर हैं। पहले त्रिभुज की भुजा AE दूसरे त्रिभुज की भुजा CE से मेल खाती है, जिसका अर्थ है AE = CE। इसी प्रकार BE = DE. समान खंडों का प्रत्येक जोड़ा एक समांतर चतुर्भुज का एक विकर्ण बनाता है। इस प्रकार यह सिद्ध हो गया है समांतर चतुर्भुज के विकर्णों को उनके प्रतिच्छेदन बिंदु द्वारा विभाजित किया जाता है.