Paralelograms ir četrstūris, kuram ir pretējās puses paralēli, t.i. gulēt uz paralēlām līnijām

Paralelograma īpašības: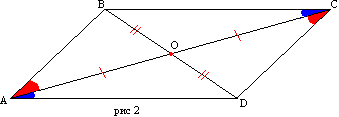
22. teorēma. Paralelograma pretējās malas ir vienādas.
Pierādījums. Paralelogramā ABCD ievelkam diagonāli AC. Trijstūri ACD un ACB ir kongruenti, jo tiem ir kopīga mala AC un divi vienādu leņķu pāri. tai blakus: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (kā šķērsām leņķi ar paralēlām līnijām AD un BC). Tas nozīmē, ka AB = CD un BC = AD, kā vienādu trīsstūru atbilstošās malas utt. No šo trīsstūru vienādības arī izriet, ka attiecīgie trīsstūru leņķi ir vienādi:
23. teorēma. Paralelograma pretējie leņķi ir vienādi: ∠ A=∠ C un ∠ B=∠ D.
Pirmā pāra vienādība nāk no trijstūri ABD un CBD, bet otrā - ABC un ACD.
24. teorēma. Paralelograma blakus leņķi, t.i. leņķi, kas atrodas blakus vienai pusei, summējas līdz 180 grādiem.
Tas ir tāpēc, ka tie ir iekšējie vienpusēji leņķi.
25. teorēma. Paralelograma diagonāles krustošanās punktā sadala viena otru uz pusēm.
Pierādījums. Apsveriet trīsstūrus BOC un AOD. Saskaņā ar pirmo īpašību AD=BC ∠ OAD=∠ OCB un ∠ ODA=∠ OBC, kas atrodas šķērsām paralēlām taisnēm AD un BC. Tāpēc trijstūri BOC un AOD ir vienādi sānu un blakus leņķos. Tas nozīmē, ka BO=OD un AO=OS, tāpat kā vienādu trīsstūru atbilstošās malas utt.

Paralelograma zīmes
26. teorēma. Ja četrstūra pretējās malas ir vienādas pa pāriem, tad tas ir paralelograms.
Pierādījums. Lai četrstūra ABCD malas AD un BC, AB un CD ir attiecīgi vienādas (2. att.). Zīmēsim diagonāli AC. Trijstūri ABC un ACD ir vienādi no trim malām. Tad leņķi BAC un DCA ir vienādi, un tāpēc AB ir paralēls CD. Malu BC un AD paralēlisms izriet no leņķu vienādības CAD un ACB.
27. teorēma. Ja četrstūra pretējie leņķi pa pāriem ir vienādi, tad tas ir paralelograms.
Pieņemsim, ka ∠ A=∠ C un ∠ B=∠ D. Tā kā ∠ A+∠ B+∠ C+∠ D=360 o, tad ∠ A+∠ B=180 o un malas AD un BC ir paralēlas (pamatojoties uz taisnu paralēlismu). Pierādīsim arī malu AB un CD paralēlismu un secināsim, ka ABCD pēc definīcijas ir paralelograms.
28. teorēma. Ja četrstūra blakus stūri, t.i. Vienai malai blakus esošie leņķi summējas līdz 180 grādiem, tad tas ir paralelograms.
Ja iekšējie vienpusējie leņķi summējas līdz 180 grādiem, tad taisnās līnijas ir paralēlas. Tātad AB ir paralēla CD un BC ir paralēla AD. Četrstūris pēc definīcijas izrādās paralelograms.
29. teorēma. Ja četrstūra diagonāles krustpunktā dala viena otru, tad četrstūris ir paralelograms.
Pierādījums. Ja AO = OC, BO = OD, tad trijstūri AOD un BOC ir vienādi, jo tiem virsotnē O ir vienādi (vertikāli) leņķi, kas ietverti starp vienādu malu pāriem. No trīsstūru vienādības secinām, ka AD un BC ir vienādi. Arī malas AB un CD ir vienādas, un četrstūris saskaņā ar 1. kritēriju izrādās paralelograms.
30. teorēma. Ja četrstūrim ir vienādu, paralēlu malu pāris, tad tas ir paralelograms.
Lai četrstūra ABCD malas AB un CD ir paralēlas un vienādas. Zīmēsim diagonāles AC un BD. No šo līniju paralēlisma izriet, ka šķērsleņķi ABO = CDO un BAO = OCD ir vienādi. Trijstūri ABO un CDO ir vienādi sānu un blakus leņķos. Tāpēc AO=OS, VO=ОD, t.i. Diagonāles tiek dalītas uz pusēm ar krustpunktu, un četrstūris saskaņā ar 4. kritēriju izrādās paralelograms.

Ģeometrijā tiek aplūkoti īpaši paralelogramu gadījumi.

1. Paralelograma definīcija.

Ja mēs krustojam paralēlu taisnu pāri ar citu paralēlu līniju pāri, mēs iegūstam četrstūri, kura pretējās malas ir paralēlas pa pāriem.

Četrstūros ABDC un EFNM (224. att.) ВD || AC un AB || CD;

EF || MN un EM || FN.

Četrstūri, kura pretējās malas ir paralēlas pa pāriem, sauc par paralelogramu.

2. Paralelograma īpašības.

Teorēma. Paralelograma diagonāle sadala to divos vienādos trīsstūros.

Lai ir paralelograms ABDC (225. att.), kurā AB || CD un maiņstrāva || ВD.

Jums jāpierāda, ka diagonāle to sadala divos vienādos trīsstūros.

Uzzīmēsim diagonāli CB paralelogramā ABDC. Pierādīsim, ka \(\Delta\)CAB = \(\Delta\)СДВ.

ZA mala ir kopīga šiem trijstūriem; ∠ABC = ∠BCD, kā iekšējie šķērsleņķi ar paralēlu AB un CD un secantu CB; ∠ACB = ∠СВD, tāpat kā iekšējie šķērsleņķi ar paralēlu maiņstrāvu un BD un secantu CB.

Tādējādi \(\Delta\)CAB = \(\Delta\)СДВ.

Tādā pašā veidā var pierādīt, ka diagonāle AD sadalīs paralelogramu divos vienādos trīsstūros ACD un ABD.

Sekas:

1 . Paralelograma pretējie leņķi ir vienādi viens ar otru.

∠A = ∠D, tas izriet no trīsstūru CAB un CDB vienādības.

Tāpat ∠C = ∠B.

2. Paralelograma pretējās malas ir vienādas viena ar otru.

AB = CD un AC = BD, jo tās ir vienādu trīsstūru malas un atrodas pretī vienādiem leņķiem.

2. teorēma. Paralelograma diagonāles to krustpunktā ir sadalītas uz pusēm.

Pieņemsim, ka BC un AD ir paralelograma ABC diagonāles (226. att.). Pierādīsim, ka AO = OD un CO = OB.

Lai to izdarītu, salīdziniet dažus pretēji izvietotu trīsstūru pāri, piemēram, \(\Delta\)AOB un \(\Delta\)COD.

Šajos trīsstūros AB = CD, tāpat kā paralelograma pretējās malas;

∠1 = ∠2, kā iekšējie leņķi, kas atrodas šķērsām ar paralēli AB un CD un nogriezni AD;

∠3 = ∠4 tā paša iemesla dēļ, jo AB || CD un SV ir viņu sekanti.

No tā izriet, ka \(\Delta\)AOB = \(\Delta\)СOD. Un vienādos trīsstūros vienādas malas atrodas pretī vienādiem leņķiem. Tāpēc AO = OD un CO = OB.

3. teorēma. Leņķu summa, kas atrodas blakus paralelograma vienai malai, ir vienāda ar 180°.

Paralelogramā ABCD novelkam diagonāli AC un iegūstam divus trijstūrus ABC un ADC.

Trijstūri ir vienādi, jo ∠1 = ∠4, ∠2 = ∠3 (šķērsleņķi paralēlām līnijām), un mala AC ir kopīga.
No vienādības \(\Delta\)ABC = \(\Delta\)ADC izriet, ka AB = CD, BC = AD, ∠B = ∠D.

Vienai malai blakus esošo leņķu summa, piemēram, leņķi A un D, ​​ir vienāda ar 180° kā vienpusēji leņķi paralēlām līnijām.

Paralelograms ir četrstūris, kura pretējās malas ir paralēlas pa pāriem. Nākamajā attēlā parādīts paralelograms ABCD. Tam ir AB mala paralēla malai CD un mala BC paralēla malai AD.

Kā jūs, iespējams, uzminējāt, paralelograms ir izliekts četrstūris. Apskatīsim paralelograma pamatīpašības.

Paralelograma īpašības

1. Paralelogramā pretējie leņķi un pretējās malas ir vienādi. Pierādīsim šo īpašību - apsveriet paralelogramu, kas parādīts nākamajā attēlā.

Diagonāle BD sadala to divos vienādos trīsstūros: ABD un CBD. Tie ir vienādi gar malu BD un diviem tai blakus esošajiem leņķiem, jo ​​leņķi atrodas šķērsām paralēlu līniju BC un AD un attiecīgi AB un CD šķērsgriezumā BD. Tāpēc AB = CD un
BC = AD. Un no leņķu 1, 2, 3 un 4 vienādības izriet, ka leņķis A = leņķis1 + leņķis3 = leņķis2 + leņķis4 = leņķis C.

2. Paralelograma diagonāles tiek dalītas uz pusēm ar krustpunktu. Lai punkts O ir paralelograma ABCD diagonāļu AC un BD krustpunkts.

Tad trīsstūris AOB un trijstūris COD ir vienādi viens ar otru gar sānu un diviem blakus leņķiem. (AB = CD, jo tās ir paralelograma pretējās malas. Un leņķis1 = leņķis2 un leņķis3 = leņķis4 ir kā šķērsām leņķi, kad taisnes AB un CD krustojas attiecīgi ar sekantiem AC un BD.) No tā izriet, ka AO = OC un OB = OD, kas un bija jāpierāda.

Visas galvenās īpašības ir attēlotas sekojošos trīs attēlos.

Nodarbības kopsavilkums.

Algebra 8. klase

Skolotājs Sysoy A.K.

Skola 1828

Nodarbības tēma: “Paralelogramma un tās īpašības”

Nodarbības veids: kombinēts

Nodarbības mērķi:

1) Nodrošināt jauna jēdziena - paralelograma un tā īpašību asimilāciju

2) Turpināt attīstīt ģeometrisko uzdevumu risināšanas prasmes un iemaņas;

3) Matemātiskās runas kultūras attīstība

Nodarbības plāns:

1. Laika organizēšana

(1. slaids)

Slaidā ir parādīts Lūisa Kerola paziņojums. Skolēni tiek informēti par nodarbības mērķi. Tiek pārbaudīta skolēnu gatavība stundai.

2. Zināšanu papildināšana

(2. slaids)

Uz tāfeles ir uzdevumi mutiskajam darbam. Skolotāja aicina skolēnus aizdomāties par šīm problēmām un pacelt roku tiem, kas saprot, kā problēmu risināt. Pēc divu uzdevumu atrisināšanas pie tāfeles, lai pierādītu teorēmu par leņķu summu, tiek izsaukts students, kurš patstāvīgi veido papildu konstrukcijas uz zīmējuma un teorēmu pierāda mutiski.

Studenti izmanto formulu daudzstūra leņķu summai:

3. Galvenā daļa

(3. slaids)

Paralelograma definīcija uz tāfeles. Skolotājs runā par jaunu figūru un formulē definīciju, veicot nepieciešamos paskaidrojumus, izmantojot zīmējumu. Pēc tam prezentācijas rūtainajā daļā, izmantojot marķieri un lineālu, viņš parāda, kā uzzīmēt paralelogramu (iespējami vairāki gadījumi)

(4. slaids)

Skolotājs formulē paralelograma pirmo īpašību. Aicina skolēnus pēc zīmējuma pastāstīt, kas ir dots un kas jāpierāda. Pēc tam dotais uzdevums parādās uz tāfeles. Skolēni min (varbūt ar skolotāja palīdzību), ka nepieciešamās vienādības ir jāpierāda caur trijstūri vienādībām, kuras var iegūt, zīmējot diagonāli (uz tāfeles parādās diagonāle). Tālāk skolēni uzmin, kāpēc trīsstūri ir vienādi, un nosauc zīmi, ka trijstūri ir vienādi (parādās atbilstošā forma). Viņi mutiski paziņo faktus, kas ir nepieciešami, lai trijstūri būtu vienādi (nosaucot tos, parādās atbilstoša vizualizācija). Tālāk studenti formulē kongruentu trīsstūru īpašību, kas parādās kā pierādījuma 3. punkts, un pēc tam patstāvīgi izpilda teorēmas pierādījumu mutiski.

(5. slaids)

Skolotājs formulē paralelograma otro īpašību. Uz tāfeles parādās paralelograma zīmējums. Skolotājs iesaka izmantot attēlu, lai pastāstītu, kas ir dots un kas ir jāpierāda. Pēc tam, kad studenti pareizi ziņo, kas ir dots un kas ir jāpierāda, parādās teorēmas nosacījums. Studenti uzmin, ka diagonāļu daļu vienādību var pierādīt ar trīsstūru vienādībuAOB Un C.O.D.. Izmantojot paralelograma iepriekšējo īpašību, var uzminēt, ka malas ir vienādasAB Un CD. Tad viņi saprot, ka jāatrod vienādi leņķi un, izmantojot paralēlo līniju īpašības, jāpierāda vienādām malām blakus esošo leņķu vienādība. Šie posmi ir vizualizēti slaidā. Teorēmas patiesums izriet no trīsstūru vienādības - skolēni to pasaka un slaidā parādās atbilstoša vizualizācija.

(6. slaids)

Skolotājs formulē paralelograma trešo īpašību. Atkarībā no laika, kas atlicis līdz stundas beigām, skolotājs var dot iespēju skolēniem pašiem pierādīt šo īpašību vai arī aprobežoties ar tā formulēšanu, un pašu pierādīšanu atstāt skolēniem kā mājasdarbu. Pierādījumu var balstīt uz ierakstīta daudzstūra leņķu summu, kas tika atkārtota nodarbības sākumā, vai uz divu paralēlu taisnu iekšējo vienpusējo leņķu summuAD Un B.C., un, piemēram, sekantsAB.

4. Materiāla nostiprināšana

Šajā posmā skolēni problēmu risināšanai izmanto iepriekš apgūtās teorēmas. Studenti izvēlas idejas problēmas risināšanai patstāvīgi. Jo iespējamie varianti Dizaina ir daudz un tie visi ir atkarīgi no tā, kā skolēni meklēs problēmas risinājumu, nav problēmu risinājuma vizualizācijas, un studenti patstāvīgi sastāda katru risinājuma posmu uz atsevišķas tāfeles ar risinājuma ierakstīšana piezīmju grāmatiņā.

(7. slaids)

Parādās uzdevuma nosacījums. Skolotājs iesaka formulēt “Dots” atbilstoši nosacījumam. Kad skolēni pareizi pierakstījuši īsu nosacījumu, uz tāfeles parādās “Dots”. Problēmas risināšanas process varētu izskatīties šādi:

Uzzīmēsim augstumu BH (vizualizēts)

Trijstūris AHB ir taisnleņķa trīsstūris. Leņķis A vienāds ar leņķi C un vienāds ar 30 0 (atbilstoši pretējo leņķu īpašībai paralelogramā). 2BH =AB (pēc kājas, kas atrodas pretī 30 0 leņķim taisnleņķa trijstūrī). Tātad AB = 13 cm.

AB = CD, BC = AD (atbilstoši pretējo malu īpašībai paralelogramā) Tātad AB = CD = 13 cm. Tā kā paralelograma perimetrs ir 50 cm, tad BC = AD = (50 – 26): 2 = 12 cm.

Atbilde: AB = CD = 13 cm, BC = AD = 12 cm.

(8. slaids)

Parādās uzdevuma nosacījums. Skolotājs iesaka formulēt “Dots” atbilstoši nosacījumam. Pēc tam ekrānā parādās “Given”. Izmantojot sarkanās līnijas, tiek izcelts četrstūris, par kuru jums jāpierāda, ka tas ir paralelograms. Problēmas risināšanas process varētu izskatīties šādi:

Jo BK un MD ir perpendikulāras vienai taisnei, tad taisnes BK un MD ir paralēlas.

Caur blakus leņķiem var parādīt, ka iekšējo vienpusējo leņķu summa pie taisnēm BM un KD un nogriežņa MD ir vienāda ar 180 0. Tāpēc šīs līnijas ir paralēlas.

Tā kā četrstūrim BMDK ir pa pāriem paralēlas pretējās malas, tad šis četrstūris ir paralelograms.

5. Nodarbības beigas. Rezultātu uzvedība.

(8. slaids)

Slaidā parādās jautājumi par jauno tēmu, uz kuriem skolēni atbild.