समांतर चतुर्भुज एक चतुर्भुज है जिसमें होता है विपरीत दिशाएंसमानांतर, यानी समानांतर रेखाओं पर लेटें

समांतर चतुर्भुज के गुण: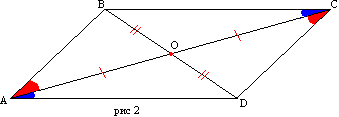
प्रमेय 22. समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।
सबूत। समांतर चतुर्भुज ABCD में हम एक विकर्ण AC बनाते हैं। त्रिभुज ACD और ACB सर्वांगसम हैं, क्योंकि इनकी एक भुजा AC और समान कोणों के दो जोड़े हैं। इसके समीप: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (समानांतर रेखाओं AD और BC के साथ क्रॉसस्वाइज़ कोण के रूप में)। इसका मतलब है कि AB = CD और BC = AD, समान त्रिभुजों की संगत भुजाओं के रूप में, आदि। इन त्रिभुजों की समानता से यह भी पता चलता है कि त्रिभुजों के संगत कोण बराबर हैं:
प्रमेय 23. समांतर चतुर्भुज के विपरीत कोण बराबर हैं: ∠ A=∠ C और ∠ B=∠ D.
पहली जोड़ी की समानता त्रिभुज ABD और CBD की समानता से आती है, और दूसरी - ABC और ACD की समानता से आती है।
प्रमेय 24. समांतर चतुर्भुज के आसन्न कोण, अर्थात् एक तरफ के निकटवर्ती कोणों का योग 180 डिग्री होता है।
ऐसा इसलिए है क्योंकि वे आंतरिक एक तरफा कोण हैं।
प्रमेय 25. समांतर चतुर्भुज के विकर्ण एक दूसरे को उनके प्रतिच्छेदन बिंदु पर समद्विभाजित करते हैं।
सबूत। त्रिभुज BOC और AOD पर विचार करें। पहली संपत्ति के अनुसार AD=BC ∠ OAD=∠ OCB और ∠ ODA=∠OBC समानांतर रेखाओं AD और BC के लिए आड़े-तिरछे पड़े हैं। इसलिए, त्रिभुज BOC और AOD भुजा और आसन्न कोणों में बराबर हैं। इसका मतलब है BO=OD और AO=OS, जैसे समान त्रिभुजों की संगत भुजाएँ, आदि।

समांतर चतुर्भुज के लक्षण
प्रमेय 26. यदि किसी चतुर्भुज की सम्मुख भुजाएँ जोड़े में बराबर हों, तो वह एक समांतर चतुर्भुज होता है।
सबूत। मान लीजिए चतुर्भुज ABCD की भुजाएँ क्रमशः AD और BC, AB और CD बराबर हैं (चित्र 2)। आइए विकर्ण AC बनाएं। त्रिभुज ABC और ACD तीन भुजाओं पर बराबर हैं। तब कोण BAC और DCA बराबर हैं और इसलिए, AB, CD के समानांतर है। भुजाओं BC और AD की समानता कोण CAD और ACB की समानता से होती है।
प्रमेय 27. यदि किसी चतुर्भुज के सम्मुख कोण जोड़े में बराबर हों, तो वह एक समांतर चतुर्भुज होता है।
माना ∠ A=∠ C और ∠ B=∠ D. क्योंकि ∠ A+∠ B+∠ C+∠ D=360 o, फिर ∠ A+∠ B=180 o और भुजाएँ AD और BC समानांतर हैं (सीधी रेखाओं की समानता के आधार पर)। हम भुजाओं AB और CD की समांतरता को भी सिद्ध करेंगे और निष्कर्ष निकालेंगे कि परिभाषा के अनुसार ABCD एक समांतर चतुर्भुज है।
प्रमेय 28. यदि चतुर्भुज के आसन्न कोने, अर्थात् एक भुजा से सटे कोणों का योग 180 डिग्री होता है, तो यह एक समांतर चतुर्भुज है।
यदि आंतरिक एकतरफ़ा कोणों का योग 180 डिग्री हो, तो सीधी रेखाएँ समानांतर होती हैं। अतः AB, CD के समानांतर है और BC, AD के समानांतर है। परिभाषा के अनुसार एक चतुर्भुज एक समांतर चतुर्भुज बन जाता है।
प्रमेय 29. यदि किसी चतुर्भुज के विकर्ण एक दूसरे को प्रतिच्छेद बिंदु पर समद्विभाजित करते हैं, तो चतुर्भुज एक समांतर चतुर्भुज होता है।
सबूत। यदि AO = OC, BO = OD है, तो त्रिभुज AOD और BOC बराबर हैं, क्योंकि शीर्ष O पर समान (ऊर्ध्वाधर) कोण हैं, जो समान भुजाओं के जोड़े के बीच घिरे हुए हैं। त्रिभुजों की समानता से हम यह निष्कर्ष निकालते हैं कि AD और BC बराबर हैं। भुजाएँ AB और CD भी बराबर हैं और मानदंड 1 के अनुसार चतुर्भुज एक समांतर चतुर्भुज बन जाता है।
प्रमेय 30. यदि किसी चतुर्भुज में समान, समानांतर भुजाओं का एक जोड़ा है, तो वह एक समांतर चतुर्भुज है।
माना चतुर्भुज ABCD की भुजाएँ AB और CD समानांतर और बराबर हैं। आइए विकर्ण AC और BD बनाएं। इन रेखाओं की समानता से यह निष्कर्ष निकलता है कि क्रॉसवाइज कोण ABO = CDO और BAO = OCD बराबर हैं। त्रिभुज ABO और CDO भुजा और आसन्न कोणों में बराबर हैं। इसलिए AO=OS, VO=ОD, अर्थात्। विकर्णों को प्रतिच्छेदन बिंदु द्वारा आधे में विभाजित किया जाता है और चतुर्भुज मानदंड 4 के अनुसार एक समांतर चतुर्भुज बन जाता है।

ज्यामिति में, समांतर चतुर्भुज के विशेष मामलों पर विचार किया जाता है।

1. समांतर चतुर्भुज की परिभाषा.

यदि हम समानांतर रेखाओं के एक जोड़े को समानांतर रेखाओं के दूसरे जोड़े के साथ काटते हैं, तो हमें एक चतुर्भुज मिलता है जिसकी विपरीत भुजाएँ जोड़े में समानांतर होती हैं।

चतुर्भुज ABDC और EFNM में (चित्र 224) ВD || एसी और एबी || सीडी;

ईएफ || एमएन और ईएम || एफ.एन.

वह चतुर्भुज जिसकी सम्मुख भुजाएँ जोड़े में समान्तर हों, समांतर चतुर्भुज कहलाता है।

2. समांतर चतुर्भुज के गुण.

प्रमेय. एक समांतर चतुर्भुज का विकर्ण उसे दो समान त्रिभुजों में विभाजित करता है।

मान लीजिए कि एक समांतर चतुर्भुज ABDC है (चित्र 225), जिसमें AB || है सीडी और एसी || वी.डी.

आपको यह सिद्ध करना होगा कि विकर्ण इसे दो समान त्रिभुजों में विभाजित करता है।

आइए समांतर चतुर्भुज ABDC में विकर्ण CB बनाएं। आइए हम सिद्ध करें कि \(\Delta\)CAB = \(\Delta\)СДВ.

इन त्रिभुजों में भुजा NE उभयनिष्ठ है; ∠ABC = ∠BCD, समानांतर AB और CD और छेदक CB के साथ आंतरिक क्रॉसवाइज कोण के रूप में; ∠ACB = ∠СВD, समानांतर AC ​​और BD और छेदक CB के साथ आंतरिक क्रॉसवाइज कोण की तरह।

इसलिए \(\Delta\)CAB = \(\Delta\)СДВ.

इसी प्रकार, कोई यह सिद्ध कर सकता है कि विकर्ण AD समांतर चतुर्भुज को दो समान त्रिभुजों ACD और ABD में विभाजित करेगा।

नतीजे:

1 . समांतर चतुर्भुज के सम्मुख कोण एक दूसरे के बराबर होते हैं।

∠A = ∠D, यह त्रिभुज CAB और CDB की समानता से अनुसरण करता है।

इसी प्रकार, ∠C = ∠B.

2. समांतर चतुर्भुज की सम्मुख भुजाएँ एक दूसरे के बराबर होती हैं।

AB = CD और AC = BD, चूँकि ये समान त्रिभुजों की भुजाएँ हैं और समान कोणों के विपरीत स्थित हैं।

प्रमेय 2. समांतर चतुर्भुज के विकर्ण उनके प्रतिच्छेदन बिंदु पर आधे में विभाजित होते हैं।

मान लीजिए BC और AD समांतर चतुर्भुज ABC के विकर्ण हैं (चित्र 226)। आइए हम सिद्ध करें कि AO = OD और CO = OB है।

ऐसा करने के लिए, विपरीत स्थित त्रिभुजों के कुछ युग्मों की तुलना करें, उदाहरण के लिए \(\Delta\)AOB और \(\Delta\)СOD.

इन त्रिभुजों में AB = CD, समांतर चतुर्भुज की विपरीत भुजाओं की तरह;

∠1 = ∠2, समानांतर AB और CD और छेदक AD के साथ आड़े पड़ने वाले आंतरिक कोण के रूप में;

∠3 = ∠4 उसी कारण से, चूँकि AB || सीडी और एसवी उनके सचिव हैं।

यह इस प्रकार है कि \(\Delta\)AOB = \(\Delta\)СOD. और समान त्रिभुजों में, समान भुजाएँ समान कोणों के विपरीत होती हैं। इसलिए, AO = OD और CO = OB।

प्रमेय 3. एक समांतर चतुर्भुज की एक भुजा से सटे कोणों का योग बराबर होता है 180°.

समांतर चतुर्भुज ABCD में हम एक विकर्ण AC बनाते हैं और दो त्रिभुज ABC और ADC प्राप्त करते हैं।

त्रिभुज बराबर हैं, क्योंकि ∠1 = ∠4, ∠2 = ∠3 (समानांतर रेखाओं को काटने वाले कोण), और भुजा AC उभयनिष्ठ है।
समानता \(\Delta\)ABC = \(\Delta\)ADC से यह निष्कर्ष निकलता है कि AB = CD, BC = AD, ∠B = ∠D.

एक तरफ से सटे कोणों का योग, उदाहरण के लिए कोण ए और डी, समानांतर रेखाओं के लिए एक तरफा कोण के रूप में 180° के बराबर होता है।

समांतर चतुर्भुज एक चतुर्भुज है जिसकी सम्मुख भुजाएँ जोड़े में समांतर होती हैं। निम्नलिखित चित्र समांतर चतुर्भुज ABCD दर्शाता है। इसकी भुजा AB, भुजा CD के समांतर और भुजा BC, भुजा AD के समांतर है।

जैसा कि आपने अनुमान लगाया होगा, एक समांतर चतुर्भुज एक उत्तल चतुर्भुज है। आइए समांतर चतुर्भुज के मूल गुणों पर विचार करें।

समांतर चतुर्भुज के गुण

1. एक समांतर चतुर्भुज में सम्मुख कोण और सम्मुख भुजाएँ बराबर होती हैं। आइए इस गुण को सिद्ध करें - निम्नलिखित चित्र में प्रस्तुत समांतर चतुर्भुज पर विचार करें।

विकर्ण BD इसे दो समान त्रिभुजों में विभाजित करता है: ABD और CBD। वे भुजा BD और उसके निकटवर्ती दो कोणों के अनुदिश बराबर हैं, क्योंकि ये कोण क्रमशः समानांतर रेखाओं BC और AD और AB और CD के छेदक BD पर क्रॉसवाइज स्थित हैं। इसलिए AB = CD और
बीसी = एडी. और कोण 1, 2, 3 और 4 की समानता से यह निष्कर्ष निकलता है कि कोण A = कोण1 + कोण3 = कोण2 + कोण4 = कोण C.

2. समांतर चतुर्भुज के विकर्णों को प्रतिच्छेदन बिंदु द्वारा आधे में विभाजित किया जाता है। मान लीजिए बिंदु O समांतर चतुर्भुज ABCD के विकर्ण AC और BD का प्रतिच्छेदन बिंदु है।

फिर त्रिभुज AOB और त्रिभुज COD, भुजा और दो आसन्न कोणों के अनुदिश एक दूसरे के बराबर हैं। (AB = CD क्योंकि ये समांतर चतुर्भुज की विपरीत भुजाएँ हैं। और कोण1 = कोण2 और कोण3 = कोण4 आड़े कोण की तरह हैं जब रेखाएँ AB और CD क्रमशः छेदक AC और BD पर प्रतिच्छेद करती हैं।) इससे यह निष्कर्ष निकलता है कि AO = OC और OB = OD, जिसे सिद्ध करने की आवश्यकता है।

सभी मुख्य गुण निम्नलिखित तीन आंकड़ों में दर्शाए गए हैं।

पाठ सारांश.

बीजगणित आठवीं कक्षा

शिक्षक सिसोय ए.के.

स्कूल 1828

पाठ विषय: "समांतर चतुर्भुज और उसके गुण"

पाठ का प्रकार: संयुक्त

पाठ मकसद:

1) एक नई अवधारणा को आत्मसात करना सुनिश्चित करें - एक समांतर चतुर्भुज और उसके गुण

2) ज्यामितीय समस्याओं को हल करने के लिए कौशल और क्षमताओं का विकास जारी रखें;

3) गणितीय भाषण की संस्कृति का विकास

शिक्षण योजना:

1. आयोजन का समय

(स्लाइड 1)

स्लाइड में लुईस कैरोल का एक बयान दिखाया गया है। छात्रों को पाठ के उद्देश्य के बारे में सूचित किया जाता है। पाठ के लिए छात्रों की तत्परता की जाँच की जाती है।

2. ज्ञान को अद्यतन करना

(स्लाइड 2)

बोर्ड पर मौखिक कार्य के लिए कार्य हैं। शिक्षक छात्रों को इन समस्याओं के बारे में सोचने और उन लोगों की ओर हाथ उठाने के लिए आमंत्रित करता है जो समझते हैं कि समस्या को कैसे हल किया जाए। दो समस्याओं को हल करने के बाद, एक छात्र को कोणों के योग पर प्रमेय को सिद्ध करने के लिए बोर्ड पर बुलाया जाता है, जो स्वतंत्र रूप से ड्राइंग पर अतिरिक्त निर्माण करता है और प्रमेय को मौखिक रूप से सिद्ध करता है।

छात्र बहुभुज के कोणों के योग के लिए सूत्र का उपयोग करते हैं:

3. मुख्य भाग

(स्लाइड 3)

बोर्ड पर समांतर चतुर्भुज की परिभाषा. शिक्षक एक नई आकृति के बारे में बात करता है और एक परिभाषा तैयार करता है, एक चित्र का उपयोग करके आवश्यक स्पष्टीकरण देता है। फिर, प्रस्तुति के चेकर वाले भाग पर, एक मार्कर और रूलर का उपयोग करके, वह दिखाता है कि एक समांतर चतुर्भुज कैसे बनाया जाता है (कई मामले संभव हैं)

(स्लाइड 4)

शिक्षक समांतर चतुर्भुज का पहला गुण तैयार करता है। विद्यार्थियों को ड्राइंग से यह बताने के लिए आमंत्रित करता है कि क्या दिया गया है और क्या सिद्ध करने की आवश्यकता है। इसके बाद दिया गया टास्क बोर्ड पर दिखने लगता है. छात्र अनुमान लगाते हैं (शायद शिक्षक की मदद से) कि आवश्यक समानताएँ त्रिभुजों की समानताओं के माध्यम से सिद्ध की जानी चाहिए, जिन्हें एक विकर्ण खींचकर प्राप्त किया जा सकता है (बोर्ड पर एक विकर्ण दिखाई देता है)। इसके बाद, छात्र अनुमान लगाते हैं कि त्रिकोण बराबर क्यों हैं और उस चिह्न को नाम दें कि त्रिकोण बराबर हैं (संबंधित आकृति दिखाई देती है)। वे मौखिक रूप से उन तथ्यों को संप्रेषित करते हैं जो त्रिभुजों को बराबर बनाने के लिए आवश्यक हैं (जैसा कि वे उन्हें नाम देते हैं, एक संबंधित दृश्य प्रकट होता है)। इसके बाद, छात्र सर्वांगसम त्रिभुजों का गुणधर्म तैयार करते हैं, यह प्रमाण के बिंदु 3 के रूप में प्रकट होता है, और फिर स्वतंत्र रूप से मौखिक रूप से प्रमेय का प्रमाण पूरा करते हैं।

(स्लाइड 5)

शिक्षक समांतर चतुर्भुज का दूसरा गुण बनाता है। बोर्ड पर एक समांतर चतुर्भुज का चित्र दिखाई देता है। शिक्षक चित्र का उपयोग करके यह बताने का सुझाव देते हैं कि क्या दिया गया है और क्या सिद्ध करने की आवश्यकता है। छात्रों द्वारा सही ढंग से रिपोर्ट करने के बाद कि क्या दिया गया है और क्या सिद्ध करने की आवश्यकता है, प्रमेय की स्थिति सामने आती है। विद्यार्थियों का अनुमान है कि त्रिभुजों की समानता से विकर्णों के भागों की समानता सिद्ध की जा सकती हैएओबीऔर सी.ओ.डी.. समांतर चतुर्भुज की पिछली संपत्ति का उपयोग करके, कोई अनुमान लगाता है कि भुजाएँ बराबर हैंअबऔर सीडी. तब वे समझते हैं कि उन्हें समान कोण खोजने की आवश्यकता है और, समानांतर रेखाओं के गुणों का उपयोग करके, समान भुजाओं से सटे कोणों की समानता साबित करें। इन चरणों को स्लाइड पर दर्शाया गया है। प्रमेय की सत्यता त्रिभुजों की समानता से आती है - छात्र इसे कहते हैं और स्लाइड पर संबंधित दृश्य दिखाई देता है।

(स्लाइड 6)

शिक्षक समांतर चतुर्भुज का तीसरा गुण तैयार करता है। पाठ के अंत तक बचे समय के आधार पर, शिक्षक छात्रों को इस संपत्ति को स्वयं साबित करने का अवसर दे सकता है, या खुद को इसके निर्माण तक सीमित कर सकता है, और सबूत को होमवर्क के रूप में छात्रों पर छोड़ सकता है। प्रमाण एक उत्कीर्ण बहुभुज के कोणों के योग पर आधारित हो सकता है, जिसे पाठ की शुरुआत में दोहराया गया था, या दो समानांतर रेखाओं के आंतरिक एक तरफा कोणों के योग पर आधारित हो सकता हैविज्ञापनऔर ईसा पूर्व, और एक सेकेंट, उदाहरण के लिएअब.

4. सामग्री को ठीक करना

इस स्तर पर, छात्र समस्याओं को हल करने के लिए पहले से सीखे गए प्रमेयों का उपयोग करते हैं। छात्र स्वतंत्र रूप से समस्या को हल करने के लिए विचारों का चयन करते हैं। क्योंकि संभावित विकल्पबहुत सारे डिज़ाइन हैं और वे सभी इस बात पर निर्भर करते हैं कि छात्र समस्या का समाधान कैसे खोजेंगे, समस्याओं के समाधान का कोई दृश्य नहीं है, और छात्र स्वतंत्र रूप से एक अलग बोर्ड पर समाधान के प्रत्येक चरण को तैयार करते हैं समाधान को एक नोटबुक में रिकॉर्ड करना।

(स्लाइड 7)

कार्य स्थिति प्रकट होती है. शिक्षक स्थिति के अनुसार "दिया गया" तैयार करने का सुझाव देता है। छात्रों द्वारा शर्त का एक संक्षिप्त विवरण सही ढंग से लिखने के बाद, बोर्ड पर "दिया गया" दिखाई देता है। समस्या को हल करने की प्रक्रिया इस प्रकार दिख सकती है:

आइए ऊंचाई BH बनाएं (कल्पित)

त्रिभुज AHB एक समकोण त्रिभुज है। कोण ए कोण के बराबर C और 30 0 के बराबर है (समांतर चतुर्भुज में विपरीत कोणों के गुण के अनुसार)। 2BH =AB (एक समकोण त्रिभुज में 30 0 कोण के विपरीत स्थित पैर की संपत्ति के आधार पर)। अतः AB = 13 सेमी.

एबी = सीडी, बीसी = एडी (समांतर चतुर्भुज में विपरीत भुजाओं के गुण के अनुसार) तो एबी = सीडी = 13 सेमी। चूँकि समांतर चतुर्भुज का परिमाप 50 सेमी है, तो BC = AD = (50 – 26): 2 = 12 सेमी.

उत्तर: एबी = सीडी = 13 सेमी, बीसी = एडी = 12 सेमी।

(स्लाइड 8)

कार्य स्थिति प्रकट होती है. शिक्षक स्थिति के अनुसार "दिया गया" तैयार करने का सुझाव देता है। फिर स्क्रीन पर "दिया गया" दिखाई देता है। लाल रेखाओं का उपयोग करके, एक चतुर्भुज को हाइलाइट किया जाता है, जिसके बारे में आपको यह साबित करना होगा कि यह एक समांतर चतुर्भुज है। समस्या को हल करने की प्रक्रिया इस तरह दिख सकती है:

क्योंकि बीके और एमडी एक रेखा पर लंबवत हैं, तो रेखाएं बीके और एमडी समानांतर हैं।

आसन्न कोणों के माध्यम से यह दिखाया जा सकता है कि सीधी रेखाओं बीएम और केडी और छेदक एमडी पर आंतरिक एक तरफा कोणों का योग 180 0 के बराबर है। अतः ये रेखाएँ समानान्तर हैं।

चूँकि चतुर्भुज BMDK की विपरीत भुजाएँ जोड़े में समानांतर हैं, तो यह चतुर्भुज एक समांतर चतुर्भुज है।

5. पाठ का अंत. परिणामों का व्यवहार.

(स्लाइड 8)

नए विषय पर प्रश्न स्लाइड पर दिखाई देते हैं, जिनका छात्र उत्तर देते हैं।