Nodarbības tēma

• Paralelograma diagonāļu īpašības.

Nodarbības mērķi

• Iepazīstieties ar jaunām definīcijām un atcerieties dažas jau pētītas.
• Nosakiet un pierādiet paralelograma diagonāļu īpašību.
• Mācīties pielietot formu īpašības, risinot uzdevumus.
• Attīstošs – attīstīt skolēnu uzmanību, neatlaidību, neatlaidību, loģisko domāšanu, matemātisko runu.
• Izglītojoši - nodarbības laikā audziniet uzmanīgu attieksmi vienam pret otru, ieaudziniet spēju uzklausīt biedrus, savstarpēju palīdzību un neatkarību.

Nodarbības mērķi

• Pārbaudi skolēnu problēmu risināšanas prasmes.

Nodarbības plāns

1. Ievads.
2. Iepriekš pētītā materiāla atkārtošana.
3. Paralelogramma, tās īpašības un pazīmes.
4. Uzdevumu piemēri.
5. Pašpārbaude.

Ievads

"Liels zinātnisks atklājums sniedz risinājumu lielai problēmai, bet jebkuras problēmas risināšanā ir atklājuma grauds."

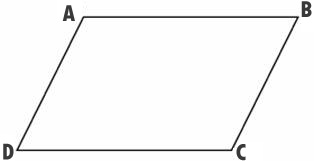
Paralelograma pretējo malu īpašība

Paralelogramam ir vienādas pretējās malas.

Pierādījums.

Dotais paralelograms ir ABCD. Un ļaujiet tās diagonālēm krustoties punktā O.
Tā kā Δ AOB = Δ COD pēc pirmā trijstūra vienādības kritērija (∠ AOB = ∠ COD, kā vertikālie, AO=OC, DO=OB, pēc paralelograma diagonāļu īpašības), tad AB=CD. Tādā pašā veidā no trīsstūru BOC un DOA vienādības izriet, ka BC = DA. Teorēma ir pierādīta.

Paralelograma pretējo leņķu īpašība

Paralelogramā pretējie leņķi ir vienādi.

Pierādījums.

Dotais paralelograms ir ABCD. Un ļaujiet tās diagonālēm krustoties punktā O.
No teorēmā pierādītā par paralelograma pretējo malu īpašībām Δ ABC = Δ CDA uz trim malām (AB=CD, BC=DA no pierādītā, AC – vispārīgi). No trīsstūru vienādības izriet, ka ∠ ABC = ∠ CDA.
Ir arī pierādīts, ka ∠ DAB = ∠ BCD, kas izriet no ∠ ABD = ∠ CDB. Teorēma ir pierādīta.

Paralelograma diagonāļu īpašība

Paralelograma diagonāles krustojas un tiek dalītas krustpunktā.

Pierādījums.

Dotais paralelograms ir ABCD. Zīmēsim diagonāli AC. Atzīmēsim uz tā vidējo O Turpinot segmentu DO, noliksim malā segmentu OB 1, kas vienāds ar DO.
Saskaņā ar iepriekšējo teorēmu AB 1 CD ir paralelograms. Tāpēc līnija AB 1 ir paralēla līdzstrāvai. Bet caur punktu A var novilkt tikai vienu taisni, kas ir paralēla līdzstrāvai. Tas nozīmē, ka līnija AB 1 sakrīt ar līniju AB.
Ir arī pierādīts, ka BC 1 sakrīt ar BC. Tas nozīmē, ka punkts C sakrīt ar C 1. paralelograms ABCD sakrīt ar paralelogramu AB 1 CD. Līdz ar to paralelograma diagonāles krustojas un krustošanās punktā tiek dalītas uz pusēm. Teorēma ir pierādīta.

Mācību grāmatās par parastās skolas(piemēram, Pogorelovā) tas ir pierādīts šādi: diagonāles sadala paralelogramu 4 trīsstūros. Apskatīsim vienu pāri un uzzināsim - tie ir vienādi: to pamati ir - pretējās puses, tam blakus esošie attiecīgie leņķi ir vienādi kā vertikālie leņķi paralēlām līnijām. Tas ir, diagonālie segmenti ir vienādi pa pāriem. Visi.

Vai tas ir viss?
Iepriekš tika pierādīts, ka krustošanās punkts sadala diagonāles uz pusēm - ja tāds pastāv. Iepriekš minētie argumenti nekādā veidā nepierāda tās pastāvēšanu. Tas ir, daļa no teorēmas “paralelograma diagonāles krustojas” paliek nepierādīta.

Smieklīgākais ir tas, ka šo daļu ir daudz grūtāk pierādīt. Tas, starp citu, izriet no vispārīgāka rezultāta: jebkuram izliektam četrstūrim būs diagonāles, kas krustojas, bet jebkuram neizliektam četrstūrim nē.

Par trijstūra vienādību gar malu un diviem blakus leņķiem (otra trijstūra vienādības zīme) un citi.

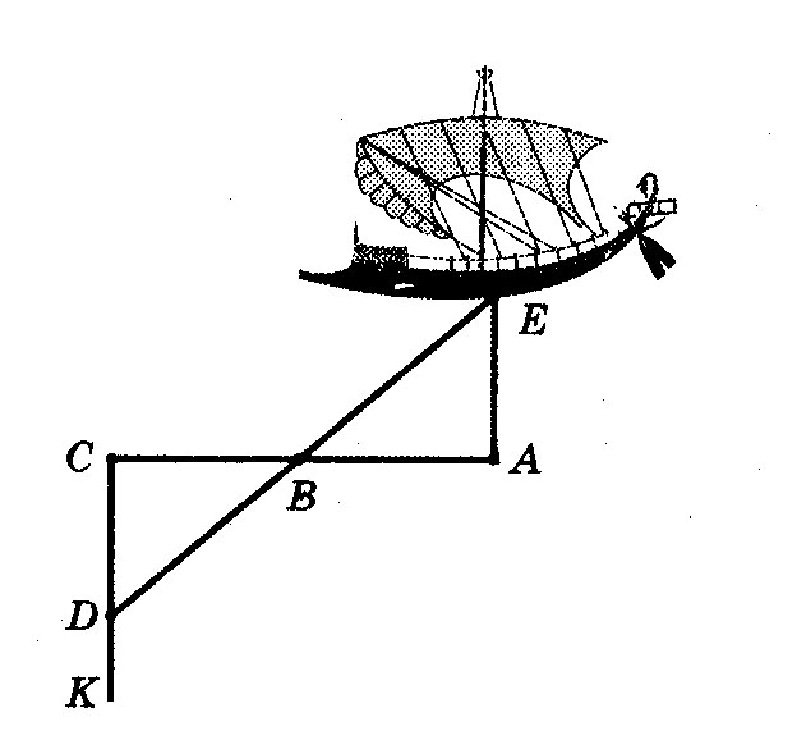
Thales atrada svarīgu teorēmu par divu trīsstūru vienādību gar malu un diviem blakus leņķiem praktiska izmantošana. Milētas ostā tika uzbūvēts attāluma mērītājs, lai noteiktu attālumu līdz kuģim jūrā. Tas sastāvēja no trim dzenām tapām A, B un C (AB = BC) un iezīmētas taisnas līnijas SC, kas bija perpendikulāra CA. Kad uz SK taisnes parādījās kuģis, mēs atradām punktu D tādu, ka punkti D, .B un E atradās vienā taisnē. Kā redzams zīmējumā, attālums CD uz zemes ir vēlamais attālums līdz kuģim.

Jautājumi

1. Vai kvadrāta diagonāles ir dalītas uz pusēm ar krustpunktu?
   
2. Vai paralelograma diagonāles ir vienādas?
3. Vai paralelograma pretējie leņķi ir vienādi?
4. Norādiet paralelograma definīciju?
5. Cik zīmju paralelogramam?
   
6. Vai rombs var būt paralelograms?
   

Izmantoto avotu saraksts

1. Kuzņecovs A.V., matemātikas skolotājs (5.-9.klase), Kijeva
2. "Viens Valsts eksāmens 2006. Matemātika. Mācību un mācību materiāli studentu sagatavošanai / Rosobrnadzor, ISOP - M.: Intellect-Center, 2006"
3. Mazur K. I. “M. I. Skanavi rediģētā krājuma galveno sacensību uzdevumu risināšana matemātikā”
4. L. S. Atanasjans, V. F. Butuzovs, S. B. Kadomcevs, E. G. Pozņaks, I. I. Judina “Ģeometrija, 7–9: mācību grāmata izglītības iestādēm”

Mēs strādājām pie nodarbības

Kuzņecovs A.V.

Poturnak S.A.

Jevgeņijs Petrovs

Jūs varat uzdot jautājumu par mūsdienu izglītību, izteikt ideju vai atrisināt aktuālu problēmu plkst Izglītības forums, kur starptautiski tiekas jaunas domas un darbības izglītības padome. Izveidojot emuārs, Jūs ne tikai uzlabosiet savu kompetenta skolotāja statusu, bet arī sniegsiet nozīmīgu ieguldījumu nākotnes skolas attīstībā. Izglītības vadītāju ģilde atver durvis augstākā līmeņa speciālistiem un aicina viņus sadarboties, veidojot labākās skolas pasaulē.

Četrstūris, kura pretējās malas ir paralēlas, ir paralelograms. Diagonāles ir taisnas līnijas, kas savieno pretējās virsotnes. To krustošanās punkts ir simetrijas centrs. Parasti paralelogramam ir divas diagonāles, D ir garā un d ir īsā.

Atrodiet paralelograma diagonāli, izmantojot kosinusa teorēmu

• Paralelograma leņķu α un β kosinusu vērtība.

D = √a^2 + b^2 — 2ab cosβ

d = √a^2 + b^2 + 2ab cosβ

D = √a^2 + b^2 + 2ab cosα

d = √a^2 + b^2 — 2ab cosα

Atrodiet paralelograma diagonāli, izmantojot vienu zināmu diagonāli un malas

Lai izmantotu šo metodi, jums jāzina:

• Paralelograma a un b malu garumi.

D = √2a^2 + 2b^2 — d^2

Lai izmantotu šo metodi, jums jāzina:

• Paralelograma laukums.
• Vienas diagonāles D vai d garums.
• Leņķis starp diagonālēm γ vai δ.

D = 2S/d sinγ = 2S/d sinδ

d = 2S/D sinγ = 2S/D sinδ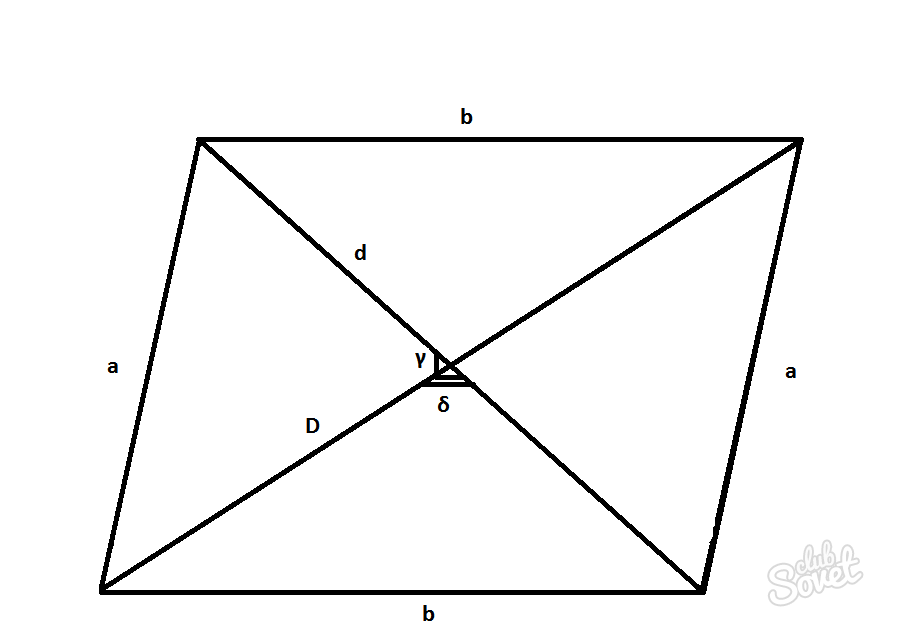

Īpašs paralelograma diagonāles garuma noteikšanas gadījums ir kvadrāts

Kvadrāts ir paralelograms, kura visas malas ir vienādas un leņķi ir 90°. Diagonāļu garumi šajā gadījumā būs vienādi ar D=d, un tos var aprēķināt, izmantojot Pitagora teorēmu.
D=d=a*√2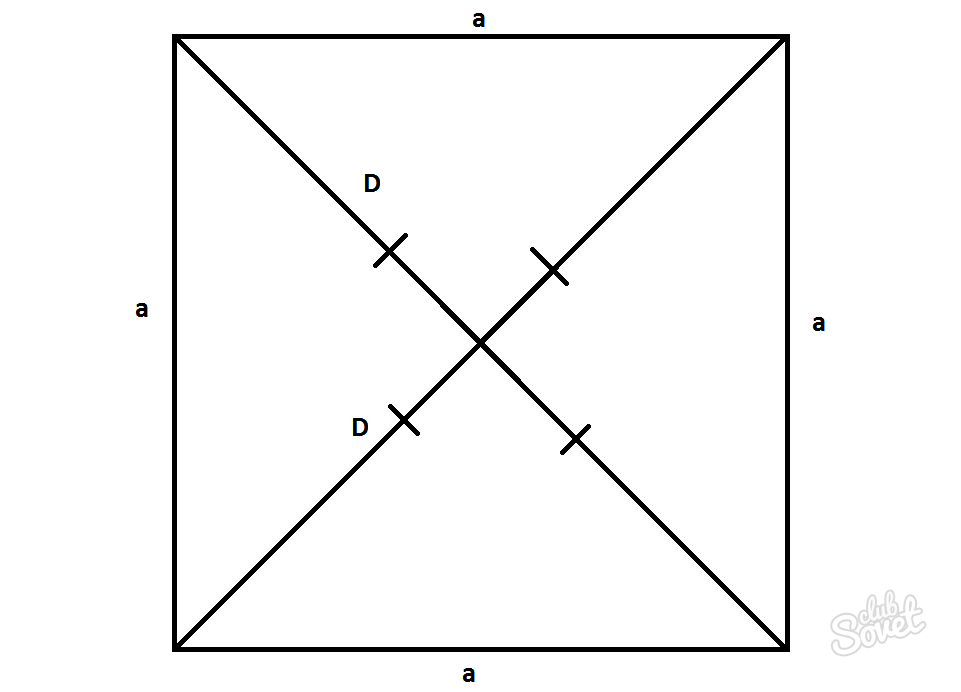

Īpašs paralelograma diagonāles garuma noteikšanas gadījums ir taisnstūris

Taisnstūris ir paralelograms, kura leņķi ir vienādi un vienādi ar 90°. Diagonāļu garumi šajā gadījumā būs vienādi ar D=d, un tos var aprēķināt, izmantojot Pitagora teorēmu.
D=d=√(a^2+b^2)

Paralelograms ir četrstūris, kura pretējās malas ir paralēlas pa pāriem. Šī definīcija jau ir pietiekama, jo no tās izriet pārējās paralelograma īpašības un tiek pierādītas teorēmu veidā.

Paralelograma galvenās īpašības ir:

• paralelograms ir izliekts četrstūris;
• Paralelogramam ir pretējās malas, kas ir vienādas pa pāriem;
• Paralelogramā pretējie leņķi ir vienādi pa pāriem;
• Paralelograma diagonāles tiek dalītas uz pusēm ar krustpunktu.

Paralēlogramma - izliekts četrstūris

Vispirms pierādīsim teorēmu, ka paralelograms ir izliekts četrstūris. Daudzstūris ir izliekts, ja neatkarīgi no tā, kura mala tiek pagarināta līdz taisnai līnijai, visas pārējās daudzstūra malas atradīsies vienā šīs taisnes pusē.

Dots paralelograms ABCD, kurā AB ir pretēja mala CD, bet BC ir pretējā mala AD. Tad no paralelograma definīcijas izriet, ka AB || CD, BC || A.D.

Paralēlajiem segmentiem nav kopīgu punktu un tie nekrustojas. Tas nozīmē, ka CD atrodas vienā AB pusē. Tā kā segments BC savieno segmenta AB punktu B ar segmenta CD punktu C un segments AD savieno citus punktus AB un CD, segmenti BC un AD arī atrodas tajā pašā līnijas AB pusē, kur atrodas CD. Tādējādi visas trīs malas - CD, BC, AD - atrodas vienā AB pusē.

Līdzīgi ir pierādīts, ka attiecībā pret paralelograma pārējām malām pārējās trīs malas atrodas vienā un tajā pašā pusē.

Pretējās malas un leņķi ir vienādi

Viena no paralelograma īpašībām ir tā Paralelogrammā pretējās malas un pretējie leņķi ir vienādi pa pāriem. Piemēram, ja ir dots paralelograms ABCD, tad tam ir AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. Šī teorēma ir pierādīta šādi.

Paralelograms ir četrstūris. Tas nozīmē, ka tam ir divas diagonāles. Tā kā paralelograms ir izliekts četrstūris, jebkurš no tiem sadala to divos trīsstūros. Paralelogramā ABCD aplūkosim trijstūrus ABC un ADC, kas iegūti, novelkot diagonāli AC.

Šiem trijstūriem ir viena kopīga mala – maiņstrāva. Leņķis BCA vienāds ar leņķi CAD kā vertikāla ar paralēlu BC un AD. Leņķi BAC un ACD arī ir vienādi ar vertikālajiem leņķiem, kad AB un CD ir paralēli. Tāpēc ∆ABC = ∆ADC divos leņķos un sānos starp tiem.

Šajos trīsstūros mala AB atbilst malai CD, un mala BC atbilst AD. Tāpēc AB = CD un BC = AD.

Leņķis B atbilst leņķim D, t.i., ∠B = ∠D. Paralelograma leņķis A ir divu leņķu summa - ∠BAC un ∠CAD. Leņķis C ir vienāds ar ∠BCA un ∠ACD. Tā kā leņķu pāri ir vienādi viens ar otru, tad ∠A = ∠C.

Tādējādi ir pierādīts, ka paralelogramā pretējās malas un leņķi ir vienādi.

Diagonāles ir sadalītas uz pusēm

Tā kā paralelograms ir izliekts četrstūris, tam ir divas diagonāles, un tās krustojas. Dots paralelograms ABCD, kura diagonāles AC un BD krustojas punktā E. Aplūkosim to veidotos trijstūrus ABE un CDE.

Šiem trijstūriem ir malas AB un CD, kas vienādas ar paralelograma pretējām malām. Leņķis ABE ir vienāds ar leņķi CDE, kas atrodas šķērsām ar paralēlām līnijām AB un CD. Tā paša iemesla dēļ ∠BAE = ∠DCE. Tas nozīmē, ka ∆ABE = ∆CDE divos leņķos un sānos starp tiem.

Varat arī pamanīt, ka leņķi AEB un CED ir vertikāli un tāpēc arī ir vienādi viens ar otru.

Tā kā trijstūri ABE un CDE ir vienādi, tad visi tiem atbilstošie elementi ir vienādi. Pirmā trīsstūra mala AE atbilst otrā trijstūra malai CE, kas nozīmē, ka AE = CE. Līdzīgi BE = DE. Katrs vienādu segmentu pāris veido paralelograma diagonāli. Tādējādi tiek pierādīts, ka Paralelograma diagonāles sadala uz pusēm pēc to krustpunkta.