V této části budeme diskutovat o kružnici opsané kolem (často se říká „okolo“) trojúhelníku. Nejprve si uveďme definici.

1. Existence a střed opsané kružnice

Zde vyvstává otázka: existuje taková kružnice pro každý trojúhelník? Ukazuje se, že ano, pro všechny. A navíc nyní zformulujeme větu, která odpovídá i na otázku, kde se nachází střed kružnice opsané.

Podívejte, takhle:

Buďme stateční a dokažme tuto větu. Pokud jste již četli téma „“ a pochopili, proč se v jednom bodě protínají tři osy, bude to pro vás jednodušší, ale pokud jste to nečetli, nebojte se: teď na to přijdeme.

Důkaz provedeme pomocí konceptu lokusu bodů (GLP).

Je například sada kuliček „geometrickým místem“ kulatých předmětů? Ne, samozřejmě, protože tam jsou kulaté...vodní melouny. Je to soubor lidí, „geometrické místo“, kteří mohou mluvit? Ani ne, protože jsou děti, které neumí mluvit. V životě je obecně obtížné najít příklad skutečného „geometrického umístění bodů“. V geometrii je to jednodušší. Zde je například přesně to, co potřebujeme:

Zde je množinou kolmice a vlastnost „ “ je „být ve stejné vzdálenosti (bodu) od konců segmentu.

Zkontrolujeme? Musíte se tedy ujistit o dvou věcech:

Spojme c a c. Pak je přímka mediánem a výškou b. To znamená - rovnoramenné - dbali jsme na to, aby každý bod ležící na odvěsně byl stejně vzdálen od bodů a.

Vezmeme střed a spojíme a. Výsledkem je medián. Ale podle podmínky není rovnoramenný pouze medián, ale také výška, tedy odvěsna. To znamená, že bod leží přesně na ose kolmice.

Všechno! Plně jsme si ověřili skutečnost, že kolmice na úsečku je místem bodů stejně vzdálených od konců úsečky.

To je všechno v pořádku, ale zapomněli jsme na circumcircle? Vůbec ne, právě jsme si připravili „odrazový můstek pro útok“.

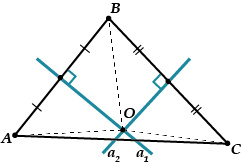
Zvažte trojúhelník. Nakreslete dvě kolmice půlící a řekněme k úsečkám a. Protnou se v nějakém bodě, který pojmenujeme.

Nyní pozor!

Bod leží na odvěsně;
bod leží na odvěsně.
A to znamená, a.

Z toho vyplývá několik věcí:

Za prvé, bod musí ležet na třetí ose kolmé k úsečce.

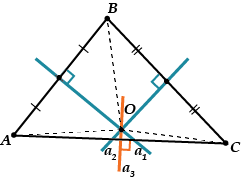
To znamená, že bodem musí procházet i odvěsna a všechny tři odvěsny se protínají v jednom bodě.

Za druhé: nakreslíme-li kružnici se středem v bodě a poloměrem, pak bude i tato kružnice procházet bodem i bodem, to znamená, že půjde o kružnici opsanou. To znamená, že již existuje, že průsečík tří kolmých os je středem kružnice opsané pro jakýkoli trojúhelník.

A poslední věc: o jedinečnosti. Je jasné (téměř), že bod lze získat jedinečným způsobem, a proto je kruh jedinečný. No, necháme „téměř“ na vaše zamyšlení. Takže jsme dokázali větu. Můžete křičet "Hurá!"

Co když se problém zeptá „najít poloměr kružnice opsané“? Nebo naopak, rádius je daný, ale potřebujete najít něco jiného? Existuje vzorec, který spojuje poloměr opsané kružnice s ostatními prvky trojúhelníku?

Definice

Kružnice \(S\) je opsána kolem mnohoúhelníku \(P\), jestliže všechny vrcholy mnohoúhelníku \(P\) leží na kružnici \(S\) .

V tomto případě se říká, že mnohoúhelník \(P\) je vepsán do kruhu.

Definice

Kolmice úsečky je přímka procházející středem dané úsečky, která je k ní kolmá.

Teorém

Každý bod kolmice úsečky je ve stejné vzdálenosti od konců úsečky.

Důkaz

Uvažujme segment \(AB\) a kolmici \(a\) k němu. Dokažme, že pro libovolný bod \(X\v a\) platí: \(AX=BX\) .

Uvažujme \(\trojúhelník AXB\) : segment \(XO\) je medián a nadmořská výška, proto \(\trojúhelník AXB\) je rovnoramenný, proto \(AX=BX\) .

Teorém

Osy kolmice ke stranám trojúhelníku se protínají v jednom bodě.

Důkaz

Zvažte \(\trojúhelník ABC\) . Nakreslete odvěsny ke stranám \(AB\) a \(AC\). Budou se protínat v bodě \(O\) .

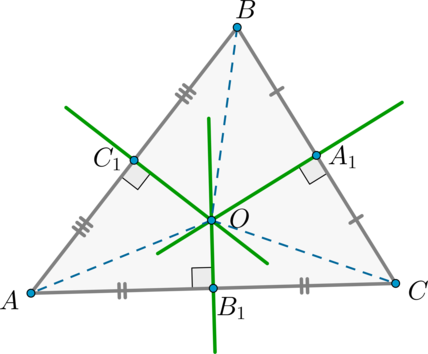
Podle předchozí věty pro odvěsnu \(C_1O\) platí: \(AO=BO\) , a pro \(B_1O\) - \(AO=CO\) . Proto \(BO=CO\) . To znamená, že \(\trojúhelník BOC\) je rovnoramenný, proto výška \(OA_1\) nakreslená k základně \(BC\) bude také mediánem. To znamená, že \(OA_1\) je kolmice na úsečku \(BC\) .

Všechny tři kolmé osy se tedy protínají v jednom bodě \(O\) .

Následek

Pokud je bod stejně vzdálený od konců úsečky, pak leží na její kolmici.

Teorém

Kolu libovolného trojúhelníku lze opsat jednu kružnici a střed opsané kružnice je průsečíkem kolmiček ke stranám trojúhelníku.

Důkaz

Z výše dokázané věty vyplývá, že \(AO=BO=CO\) . To znamená, že všechny vrcholy trojúhelníku jsou stejně vzdálené od bodu \(O\), tedy leží na stejné kružnici.

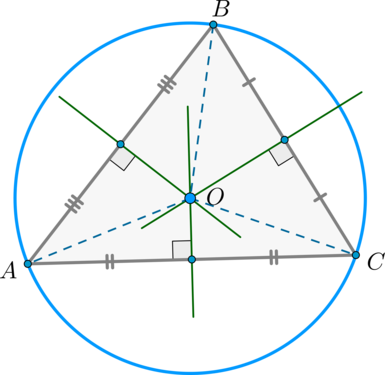
Existuje pouze jeden takový kruh. Předpokládejme, že kolem \(\trojúhelník ABC\) lze popsat další kružnici. Pak by se jeho střed měl shodovat s bodem \(O\) (protože je to jediný bod stejně vzdálený od vrcholů trojúhelníku) a poloměr by se měl rovnat vzdálenosti od středu k některému z vrcholů, tzn. \(OA\) . Protože Pokud mají tyto kružnice stejný střed a poloměr, pak se tyto kružnice také shodují.

Věta o ploše vepsaného trojúhelníku

Pokud \(a, b, c\) – strany trojúhelníku, a \(R\) je poloměr kružnice opsané kolem něj, potom plocha trojúhelníku \

Důkaz*
Po prostudování tématu „Sinesova věta“ se doporučuje seznámit se s důkazem této věty.

Označme úhel mezi stranami \(a\) a \(c\) jako \(\alpha\) . Pak \(S_(\trojúhelník)=\frac12 ac\cdot \sin \alpha\).

Podle věty o sinech \(\dfrac b(\sin\alpha)=2R\) , odkud \(\sin \alpha=\dfrac b(2R)\) . Proto, \(S_(\trojúhelník)=\dfrac(abc)(4R)\).

Teorém

Kruh lze popsat kolem čtyřúhelníku právě tehdy, když součet jeho opačných úhlů je roven \(180^\circ\) .

Důkaz

Nutnost.

Pokud lze popsat kružnici kolem čtyřúhelníku \(ABCD\), pak \(\buildrel\smile\over(ABC) + \buildrel\smile\over(ADC) = 360^\circ\), kde \(\úhel ABC + \úhel ADC = \frac(1)(2)\buildrel\smile\over(ABC) + \frac(1)(2)\buildrel\smile\over(ADC) = \frac(1 )(2)(\buildrel\smile\over(ABC) + \buildrel\smile\over(ADC)) = 180^\circ\). Pro úhly \(BCD\) a \(BAD\) je to podobné.

Přiměřenost.

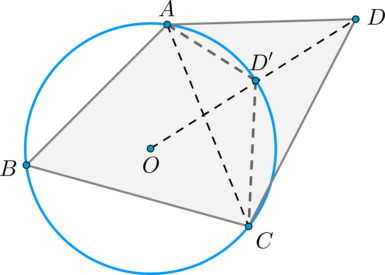
Popišme kružnici kolem trojúhelníku \(ABC\) . Nechť středem této kružnice je bod \(O\) . Na přímce procházející body \(O\) a \(D\) označíme bod \(D"\) průsečíku této přímky a kružnice Předpokládejme, že body \(D\) a \(D"\) se neshodují, pak zvažte čtyřúhelník \(CD"AD\) .

Úhly \(CD"A\) a \(CDA\) doplňují úhel \(ABC\) k \(180^\circ\) (\(\úhel CDA\) doplňuje podle podmínky a \(\úhel CD"A \) jak je dokázáno výše), jsou si tedy rovny, ale pak je součet úhlů čtyřúhelníku \(AD"CD\) větší než \(360^\circ\), což nemůže být (součet úhlů úhly tohoto čtyřúhelníku jsou součtem úhlů dvou trojúhelníků, proto se body \(D\) a \(D"\) shodují.

Komentář. Na obrázku leží bod \(D\) vně kružnice ohraničené kružnicí opsané \(\trojúhelník ABC\), avšak v případě, kdy \(D\) leží uvnitř, zůstává v platnosti i důkaz.

Teorém

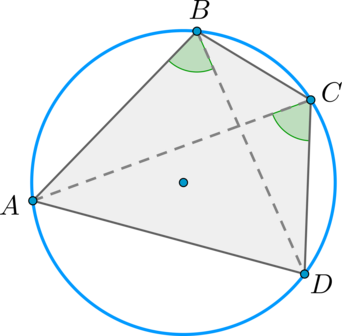
Kruh lze popsat kolem konvexního čtyřúhelníku \(ABCD\) právě tehdy, když \(\úhel ABD=\úhel ACD\) .

Důkaz

Nutnost. Pokud je kruh opsán kolem \(ABCD\), pak jsou úhly \(\úhel ABD\) a \(\úhel ACD\) vepsány a spočívají na jednom oblouku \(\buildrel\úsměv\nad(AD)\) jsou si tedy rovni.

Přiměřenost. Nechat \(\úhel ABD=\úhel ACD=\alpha\). Dokažme, že kolem \(ABCD\) lze popsat kružnici.

Popišme kružnici kolem \(\trojúhelník ABD\) . Nechť přímka \(CD\) protíná tuto kružnici v bodě \(C"\). \(\úhel ABD=\úhel AC"D \Šipka doprava \úhel AC"D=\úhel ACD\).

Proto, \(\úhel CAD=\úhel C"AD=180^\kruh-\úhel ADC-\úhel AC"D\), to je \(\triangle AC"D=\trojuhelník ACD\) podél společné strany \(AD\) a dvou sousedních úhlů (\(\úhel C"AD=\úhel CAD\) , \(\úhel ADC"=\úhel ADC\) – společný). To znamená \(DC"=DC\), to znamená, že body \(C"\) a \(C\) se shodují.

Věty

1. Pokud je rovnoběžníku opsána kružnice, pak je to obdélník (obr. 1).

2. Je-li kruh opsán kolem kosočtverce, pak je to čtverec (obr. 2).

3. Je-li kolem lichoběžníku popsána kružnice, pak je rovnoramenná (obr. 3).

Platí i obrácená tvrzení: kolem obdélníku, kosočtverce a rovnoramenného lichoběžníku lze popsat kruh, a to pouze jeden.

Důkaz

1) Nechť je kolem rovnoběžníku \(ABCD\) opsána kružnice. Potom se součty jeho opačných úhlů rovnají \(180^\circ: \quad \angle A+\angle C=180^\circ\). Ale v rovnoběžníku jsou opačné úhly stejné, protože \(\úhel A=\úhel C\) . Proto, \(\úhel A=\úhel C=90^\circ\). Takže podle definice je \(ABCD\) obdélník.

2) Nechť je kolem kosočtverce \(MNKP\) opsána kružnice. Podobně jako v předchozím bodě (protože kosočtverec je rovnoběžník) je dokázáno, že \(MNKP\) je obdélník. Ale všechny strany tohoto obdélníku jsou stejné (protože je to kosočtverec), což znamená, že \(MNKP\) je čtverec.

Opačné tvrzení je zřejmé.

3) Nechť je kolem lichoběžníku \(QWER\) opsána kružnice. Pak \(\úhel Q+\úhel E=180^\circ\). Ale z definice lichoběžníku to vyplývá \(\úhel Q+\úhel W=180^\circ\). Proto \(\úhel W=\úhel E\) . Protože úhly na základně \(WE\) lichoběžníku jsou stejné, pak je rovnoramenný.

Opačné tvrzení je zřejmé.

Zachování vašeho soukromí je pro nás důležité. Z tohoto důvodu jsme vyvinuli Zásady ochrany osobních údajů, které popisují, jak používáme a uchováváme vaše informace. Přečtěte si prosím naše zásady ochrany osobních údajů a dejte nám vědět, pokud máte nějaké dotazy.

Shromažďování a používání osobních údajů

Osobní údaje jsou údaje, které lze použít k identifikaci nebo kontaktování konkrétní osoby.

Kdykoli nás budete kontaktovat, můžete být požádáni o poskytnutí svých osobních údajů.

Níže jsou uvedeny některé příklady typů osobních údajů, které můžeme shromažďovat, a jak takové informace můžeme používat.

Jaké osobní údaje shromažďujeme:

• Když odešlete žádost na stránce, můžeme shromažďovat různé informace, včetně vašeho jména, telefonního čísla, adresy E-mailem atd.

Jak používáme vaše osobní údaje:

• Osobní údaje, které shromažďujeme, nám umožňují kontaktovat vás s jedinečnými nabídkami, akcemi a dalšími událostmi a nadcházejícími událostmi.
• Čas od času můžeme použít vaše osobní údaje k zasílání důležitých oznámení a sdělení.
• Osobní údaje můžeme také používat pro interní účely, jako je provádění auditů, analýzy dat a různé výzkumy, abychom zlepšili služby, které poskytujeme, a abychom vám poskytli doporučení týkající se našich služeb.
• Pokud se účastníte slosování o ceny, soutěže nebo podobné propagační akce, můžeme vámi poskytnuté informace použít ke správě takových programů.

Zpřístupnění informací třetím stranám

Informace, které od vás obdržíme, nesdělujeme třetím stranám.

Výjimky:

• V případě potřeby v souladu se zákonem soudní řízení, v soudních řízeních a/nebo na základě veřejných dotazů či žádostí od vládní agentury na území Ruské federace – zveřejněte své osobní údaje. Můžeme také zveřejnit informace o vás, pokud usoudíme, že takové zveřejnění je nezbytné nebo vhodné pro účely bezpečnosti, vymáhání práva nebo jiné veřejné důležité účely.
• V případě reorganizace, fúze nebo prodeje můžeme osobní údaje, které shromažďujeme, předat příslušné nástupnické třetí straně.

Ochrana osobních údajů

Přijímáme opatření – včetně administrativních, technických a fyzických – k ochraně vašich osobních údajů před ztrátou, krádeží a zneužitím, stejně jako neoprávněným přístupem, zveřejněním, pozměněním a zničením.

Respektování vašeho soukromí na úrovni společnosti

Abychom zajistili, že jsou vaše osobní údaje v bezpečí, sdělujeme našim zaměstnancům standardy ochrany soukromí a zabezpečení a přísně prosazujeme postupy ochrany osobních údajů.

>>Geometrie: Kružnice opsaná trojúhelníku. Kompletní lekce

TÉMA LEKCE: Kruh opsaný kolem trojúhelníku.

Cíle lekce:

• Prohloubte své znalosti na téma „Kruh v trojúhelníku“

Cíle lekce:

• Systematizovat znalosti na toto téma
• Připravte se na řešení problémů se zvýšenou složitostí.

Plán lekce:

1. Úvod.
2. Teoretická část.
3. Pro trojúhelník.
4. Praktická část.

Úvod.

Téma „Vepsané a opsané kružnice v trojúhelníku“ je jedním z nejobtížnějších v kurzu geometrie. Ve třídě tráví velmi málo času.

Geometrické úlohy tohoto tématu jsou zařazeny do druhé části zkoušky Jednotná státní zkouška na středoškolský kurz.
Úspěšné splnění těchto úkolů vyžaduje solidní znalost základních geometrických faktů a určitou zkušenost s řešením geometrických úloh.

Teoretická část.

Obvod mnohoúhelníku- kružnice obsahující všechny vrcholy mnohoúhelníku. Střed je bod (obvykle označovaný O) průsečíku kolmých os ke stranám mnohoúhelníku.

Vlastnosti.

Střed obvodu konvexního n-úhelníku leží v průsečíku kolmých os k jeho stranám. V důsledku toho: je-li kružnici opsána vedle n-úhelníku, pak se všechny kolmice na její strany protnou v jednom bodě (středu kružnice).
Kolem libovolného pravidelného mnohoúhelníku lze nakreslit kruh.

Pro trojúhelník.

Kruh se nazývá opsaný kolem trojúhelníku, pokud prochází všemi jeho vrcholy.

Kruh lze popsat kolem libovolného trojúhelníku a jen jeden. Jeho střed bude průsečíkem odvěsnic os.

Pro ostroúhlý trojúhelník leží střed kružnice opsané uvnitř, pro tupoúhlý - mimo trojúhelník, pro obdélníkový - uprostřed přepony.

Poloměr kružnice opsané lze zjistit pomocí vzorců:

Kde:
a,b,c- strany trojúhelníku,
α - úhel protilehlé strany a,
S- oblast trojúhelníku.

Dokázat:

t.O - průsečík odvěsnic ke stranám ΔABC

Důkaz:

1. ΔAOC - rovnoramenný, protože OA=OS (jako poloměry)
2. ΔAOC - rovnoramenný, kolmý OD - medián a výška, tzn. takže O leží na ose kolmice na stranu AC
3. Podobně je dokázáno, že t.O leží na odvěsnách ke stranám AB a BC

Q.E.D.

Komentář.

Přímka procházející středem k ní kolmého segmentu se často nazývá kolmice. V tomto ohledu se někdy říká, že střed kružnice opsané trojúhelníku leží v průsečíku odvěsnic ke stranám trojúhelníku.