प्रत्येक समलम्ब चतुर्भुज की दो भुजाएँ और दो आधार होते हैं। इस आकृति का क्षेत्रफल, परिधि या अन्य पैरामीटर जानने के लिए, आपको कम से कम एक पक्ष जानने की आवश्यकता है। इसके अलावा, अक्सर, समस्या की स्थितियों के अनुसार, एक आयताकार ट्रेपेज़ॉइड के पार्श्व पक्ष को खोजने की आवश्यकता होती है।

निर्देश

एक आयताकार समलंब ABCD बनाएं। इस आकृति की भुजाओं को क्रमशः AB और DC के रूप में लेबल करें। डीसी का पहला पार्श्व पक्ष ट्रेपेज़ॉइड की ऊंचाई के साथ मेल खाता है। यह एक आयताकार समलंब के दो आधारों पर लंबवत है।
भुजाओं को खोजने के कई तरीके हैं। इसलिए, उदाहरण के लिए, यदि समस्या को दूसरी भुजा BA और कोण ABH = 60 दिया गया है, तो ऊँचाई BH ज्ञात करके सबसे सरल तरीके से पहली ऊँचाई ज्ञात करें:
बीएच=एबी*पाप?
चूँकि BH=CD, तो CD=AB*sin?=?3AB/2

यदि, इसके विपरीत, आपको एक समलम्ब चतुर्भुज की एक भुजा दी गई है, जिसे सीडी के रूप में नामित किया गया है, और आपको इसकी भुजा AB खोजने की आवश्यकता है, तो यह समस्या थोड़े अलग तरीके से हल हो जाती है। चूँकि BH=CD, और साथ ही, BH त्रिभुज ABH के पैर का प्रतिनिधित्व करता है, हम यह निष्कर्ष निकाल सकते हैं कि भुजा AB इसके बराबर है:
AB=BH/sin?=2BH/?3

यदि कोणों का मान अज्ञात हो तो भी समस्या हल हो सकती है, बशर्ते कि दो आधार और एक भुजा AB दी गई हो। हालाँकि, इस मामले में, आप केवल साइड सीडी पा सकते हैं, जो कि ट्रेपेज़ॉइड की ऊंचाई है। प्रारंभ में, आधारों का मान जानकर, खंड AH की लंबाई ज्ञात करें। यह बड़े और छोटे आधारों के बीच अंतर के बराबर है, क्योंकि यह ज्ञात है कि BH=CD:
एएच=एडी-बीसी
फिर, पाइथागोरस प्रमेय का उपयोग करके, BH की ऊंचाई ज्ञात करें, पक्ष के बराबरसीडी:
BH=?AB^2-AH^2

यदि एक आयताकार समलम्ब चतुर्भुज का विकर्ण BD और कोण 2? है, जैसा कि चित्र 2 में दिखाया गया है, तो भुजा AB को पायथागॉरियन प्रमेय का उपयोग करके भी पाया जा सकता है। ऐसा करने के लिए, पहले आधार AD की लंबाई की गणना करें:
AD=BD*cos2?
फिर भुजा AB इस प्रकार ज्ञात करें:
एबी=?बीडी^2-एडी^2
इसके बाद त्रिभुज ABD और BCD की समानता सिद्ध कीजिए। चूँकि इन त्रिभुजों में एक उभयनिष्ठ भुजा है - विकर्ण, और साथ ही, दो कोण बराबर हैं, जैसा कि चित्र से देखा जा सकता है, तो ये आंकड़े समान हैं। इस साक्ष्य के आधार पर दूसरा पक्ष खोजें। यदि ऊपरी आधार और विकर्ण ज्ञात हैं, तो मानक कोसाइन प्रमेय का उपयोग करके सामान्य तरीके से भुजा ज्ञात करें:
c^2=a^2+b^2-2ab cos?, जहां a, b, c त्रिभुज की भुजाएं हैं, ? - भुजाओं a और b के बीच का कोण।

समलंब चतुर्भुज एक साधारण चतुर्भुज है जिसकी दोनों भुजाओं में समानता का अतिरिक्त गुण होता है, जिन्हें आधार कहा जाता है। अत: इस प्रश्न को सबसे पहले पक्ष खोजने की दृष्टि से समझना चाहिए। दूसरे, कार्य के लिए ट्रेपेज़ोइड्सकम से कम चार पैरामीटर आवश्यक हैं.

निर्देश

इस विशेष मामले में, इसके सबसे सामान्य कार्य (अनावश्यक नहीं) को इस शर्त पर विचार किया जाना चाहिए: ऊपरी और निचले आधारों की लंबाई, साथ ही विकर्णों में से एक का वेक्टर दिया गया है। समन्वय सूचकांक (ताकि लेखन गुणन जैसा न हो) इटैलिक में होगा) समाधान प्रक्रिया को ग्राफ़िक रूप से चित्रित करने के लिए, चित्र 1 बनाएं।

प्रस्तुत समस्या को समलंब चतुर्भुज ABCD पर विचार करने दें। यह आधार BC=b और AD=a की लंबाई, साथ ही वेक्टर p(px, py) द्वारा निर्दिष्ट विकर्ण AC देता है। इसकी लंबाई (मापांक) |p|=p=sqrt(((px)^2 +(py)^2)। चूँकि वेक्टर भी अक्ष के झुकाव के कोण द्वारा दिया जाता है (समस्या में - 0X), तो इसे φ (कोण CAD और इसके समानांतर कोण ACB) से निरूपित करें। इसके बाद, आपको स्कूल पाठ्यक्रम से ज्ञात कोसाइन प्रमेय को लागू करने की आवश्यकता है, इस मामले में, लंबाई CD या AB को x से निरूपित करें।

अब त्रिभुज ABC पर विचार करें। लंबाई दोनों पक्ष AC सदिश के मापांक के बराबर है |p|=p. बीसी=ए. कोसाइन प्रमेय द्वारा x^2=p^2+ a^2-2pacosф. x=AB=sqrt(p^2+ a^2-2pacosф).

हालांकि द्विघात समीकरणऔर इसकी दो जड़ें हैं, में इस मामले मेंकेवल उन्हीं का चयन करना आवश्यक है जहां विवेचक के मूल के सामने धन चिह्न हो, जबकि जानबूझकर नकारात्मक समाधानों को बाहर रखा जाए। यह इस तथ्य के कारण है कि लंबाई दोनों पक्ष ट्रेपेज़ोइड्सस्पष्ट रूप से सकारात्मक होना चाहिए.

तो, इस समस्या को हल करने के लिए एल्गोरिदम के रूप में आवश्यक समाधान प्राप्त कर लिए गए हैं। एक संख्यात्मक समाधान प्रस्तुत करने के लिए, जो कुछ बचा है वह स्थिति से डेटा को प्रतिस्थापित करना है। इस मामले में, cosф की गणना वेक्टर p=px/sqrt(px^2+py^2) के दिशा वेक्टर (ort) के रूप में की जाती है।

टिप्पणी

बेशक, अन्य प्रारंभिक डेटा भी संभव है, उदाहरण के लिए, दो विकर्ण और ट्रेपेज़ॉइड की ऊंचाई निर्दिष्ट करना। लेकिन किसी भी स्थिति में, आपको ट्रेपेज़ॉइड के आधारों के बीच की दूरी के बारे में जानकारी की आवश्यकता होगी।

ट्रैपेज़ॉइड चार कोणों वाली एक ज्यामितीय आकृति है, जिसकी दो भुजाएँ एक दूसरे के समानांतर होती हैं और आधार कहलाती हैं, और अन्य दो समानांतर नहीं होती हैं और पार्श्व कहलाती हैं।

निर्देश

आइए अलग-अलग प्रारंभिक डेटा वाली दो समस्याओं पर विचार करें। समस्या 1. पक्ष खोजें ओरसमद्विबाहु ट्रेपेज़ोइड्स, यदि परिचित हो आधारबीसी = बी, आधार AD = d और पार्श्व कोण BAD = अल्फा समाधान: लंबवत (ऊंचाई) कम करें ट्रेपेज़ोइड्स) शीर्ष B से बड़े वाले चौराहे तक आधारमी, खंड बीई प्राप्त करें। कोण के संदर्भ में सूत्र का उपयोग करके AB लिखें: AB = AE/cos(BAD) = AE/cos(अल्फा)।

एई खोजें. यह आधे में विभाजित दो आधारों की लंबाई के अंतर के बराबर होगा। तो: AE = (AD - BC)/2 = (d - b)/2. अब AB = (d - b)/(2*cos(Alpha)) खोजें। समद्विबाहु में ट्रेपेज़ोइड्सभुजाओं की लंबाई बराबर है, इसलिए, CD = AB = (d - b)/(2*cos(Alpha)).

कार्य 2. पक्ष खोजें ओर ट्रेपेज़ोइड्सएबी, यदि ऊपर वाला ज्ञात हो आधारबीसी = बी- नीचे आधारएडी = डी- ऊंचाई बीई = एच और विपरीत दिशा सीडीए पर कोण अल्फा के बराबर है: शीर्ष सी से नीचे के साथ चौराहे तक दूसरी ऊंचाई बनाएं आधारमी, खंड सीएफ प्राप्त करें। समकोण त्रिभुज CDF पर विचार करें, खोजें ओरनिम्नलिखित सूत्र का उपयोग करके FD: FD = CD*cos(CDA)। दूसरे सूत्र से सीडी की भुजा की लंबाई ज्ञात करें: सीडी = सीएफ/सिन(सीडीए)। तो: FD = CF*cos(CDA)/sin(CDA)। सीएफ = बीई = एच, इसलिए एफडी = एच*कॉस(अल्फा)/सिन(अल्फा) = एच*सीटीजी(अल्फा)।

समकोण त्रिभुज ABE पर विचार करें। इसकी भुजाओं AE और BE की लंबाई जानकर आप तीसरा ज्ञात कर सकते हैं ओर- कर्ण AB. आप भुजा BE की लंबाई जानते हैं, AE इस प्रकार ज्ञात करें: AE = AD - BC - FD = d - b - h*ctg(Alpha).का उपयोग करना अगली संपत्तिसमकोण त्रिभुज - कर्ण का वर्ग पैरों के वर्गों के योग के बराबर है - AB:AB(2) = h(2) + (d - b - h*ctg(Alpha))(2) ज्ञात करें। पक्ष का मूल्य ट्रेपेज़ोइड्सएबी बराबर है वर्गमूलमें स्थित अभिव्यक्ति से दाहिनी ओरसमानता.

सब कुछ दिलचस्प

ट्रैपेज़ॉइड एक गणितीय आकृति है, एक चतुर्भुज जिसमें विपरीत भुजाओं का एक जोड़ा समानांतर होता है और दूसरा नहीं। समलम्ब चतुर्भुज का क्षेत्रफल मुख्य संख्यात्मक विशेषताओं में से एक है। निर्देश 1 समलम्ब चतुर्भुज के क्षेत्रफल की गणना करने का मूल सूत्र इस प्रकार दिखता है...

क्षेत्रफल और परिधि किसी भी ज्यामितीय आकृतियों की मुख्य संख्यात्मक विशेषताएँ हैं। आम तौर पर स्वीकृत फ़ार्मुलों की बदौलत इन मात्राओं को खोजना सरल हो गया है, जिसके अनुसार न्यूनतम या पूर्ण अनुपस्थिति के साथ एक के माध्यम से दूसरे की गणना भी की जा सकती है...

समलंब चतुर्भुज दो समानांतर भुजाओं वाला एक चतुर्भुज है। इन पक्षों को आधार कहा जाता है। उनके अंतिम बिंदु खंडों से जुड़े होते हैं जिन्हें भुजाएँ कहते हैं। एक समद्विबाहु समलम्ब चतुर्भुज की भुजाएँ समान होती हैं।
…

समलंब चतुर्भुज एक चतुर्भुज है जिसके दो समानांतर आधार और गैर-समानांतर भुजाएँ हैं। एक आयताकार समलम्ब चतुर्भुज के एक तरफ समकोण होता है। अनुदेश 1 एक आयताकार समलम्ब चतुर्भुज का परिमाप दो आधारों की भुजाओं की लंबाई के योग के बराबर होता है...

चार कोनों वाली एक गणितीय आकृति को समलंब चतुर्भुज कहा जाता है यदि इसकी विपरीत भुजाओं का एक जोड़ा समानांतर हो और दूसरा जोड़ा समानांतर न हो। समानांतर भुजाएँसमलम्ब चतुर्भुज के आधार कहलाते हैं, अन्य दो पार्श्व आधार कहलाते हैं। एक आयताकार समलम्ब चतुर्भुज में, कोणों में से एक...

एक समलम्ब चतुर्भुज जिसकी भुजाओं की लंबाई बराबर हो और आधार समानांतर हों, समद्विबाहु या समद्विबाहु कहलाता है। दोनों विकर्ण इस प्रकार हैं ज्यामितीय आकृतिसमान लंबाई होती है, जो कि ट्रेपेज़ॉइड के ज्ञात मापदंडों के आधार पर हो सकती है...

ज्यामिति एक विज्ञान है जिसका अध्ययन स्कूल में शुरू होता है। यह सोचना भूल है कि यह जीवन में उपयोगी नहीं होगा। कभी-कभी बनाने के लिए आकृतियों के सटीक आयामों की आवश्यकता होती है, उदाहरण के लिए, एक कमरे के लिए वेब डिज़ाइन। और ट्रेपेज़ॉइड सहित विभिन्न आकृतियाँ हैं। अक्सर आपको उनकी भुजाओं या आधारों का मान ज्ञात करने की आवश्यकता होती है। आइए विस्तार से देखें कि विभिन्न आकृतियों के किसी दिए गए चतुर्भुज की पार्श्व भुजा कैसे ज्ञात की जाए, यदि उसके कोण, आधार, विकर्ण, क्षेत्रफल आदि ज्ञात हों।

यदि आधार ज्ञात हैं तो समलम्ब चतुर्भुज की भुजा कैसे ज्ञात करें?

समलंब चतुर्भुज एक चतुर्भुज है जिसकी केवल दो समानांतर भुजाएँ होती हैं। और इन गैर-प्रतिच्छेदी खंडों को इस आकृति का आधार कहा जाता है। ट्रैपेज़ विभिन्न किस्मों में आते हैं:

• आइसोलेटरल वे होते हैं जिनकी भुजाएँ बराबर होती हैं।
• आयताकार - आधार पर एक समकोण होता है।
• न्यून कोण वाला, बहुमुखी - आधार पर दो न्यून कोणों के साथ।
• अधिक-कोण, स्केलीन - आधार पर एक अधिक कोण के साथ।

यदि आपको आधारों का मान दिया गया है तो एक आयताकार समलम्ब चतुर्भुज की भुजा (ऊंचाई) ज्ञात करने के विकल्प पर विचार करें।

इस समस्या को हल करने के लिए, आपको निम्नलिखित कार्य करने होंगे:

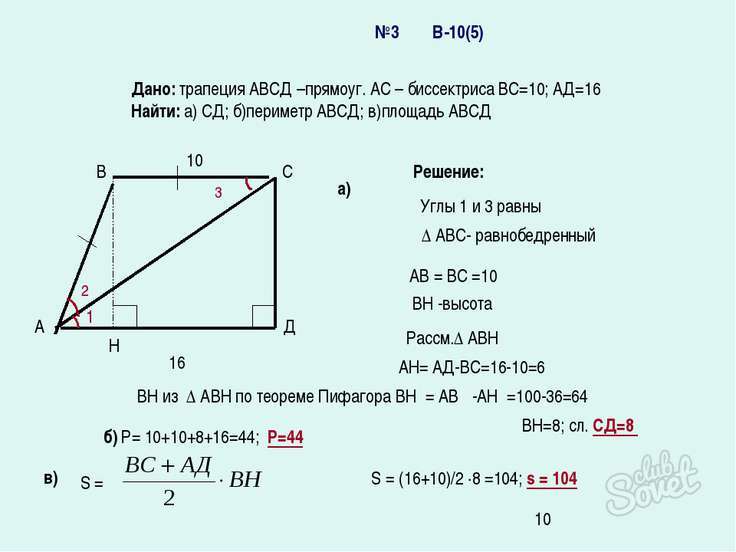
• चतुर्भुज में दूसरी ऊँचाई - BH खींचिए।
• परिणामी खंड बीएन = एसडी, क्योंकि बीसी का आधार एडी के समानांतर है।
• परिणामी त्रिभुज ABC समद्विबाहु है, क्योंकि AC एक समद्विभाजक है, आधार पर कोण क्रमशः बराबर हैं और AB = CB = 10 सेमी है।
• आइए त्रिभुज ABN पर विचार करें, वास्तव में, हम इसकी दो भुजाएँ जानते हैं: BA और AN। एएन = बीपी - सीडी = 16 - 10 = 6 सेमी।
• इसलिए, पाइथागोरस प्रमेय के अनुसार: ВН² = AB² - HA² = 64; वीएन = 8 सेमी, क्रमशः, एसडी भी 8 सेंटीमीटर के बराबर है।

इसके अलावा, यदि आप कोण VAD जानते हैं, तो SD = (AD - BC) tan α या SD = AB syn α।

बड़े पार्श्व पक्ष की गणना निम्नलिखित सूत्रों का उपयोग करके की जाती है:

• एबी² = सीडी² + (एडी - बीसी)²
• एबी = (एडी - बीसी)/कॉस ∠BAN
• एबी = सीडी/सिन ∠VAN

यदि विकर्ण, क्षेत्रफल और मध्य रेखा ज्ञात हो तो आयताकार समलंब की पार्श्व भुजा कैसे ज्ञात करें?

यदि हम समलम्ब चतुर्भुज की ऊँचाई - b, बड़ी भुजा - c, आधार - a और k, विकर्ण - d1 और d2 दर्शाते हैं। उनके बीच बड़ा कोण β है, छोटा α है, तो ऊंचाई (ट्रेपेज़ॉइड का किनारा) निम्नलिखित सूत्रों का उपयोग करके पाया जा सकता है:

बी = डी2 डी1/ (ए + के) पाप α;

या b = d2 d1/ (a + k) पाप β

यह निर्धारित करने के लिए कि बी - एक आयताकार ट्रेपेज़ॉइड का छोटा पक्ष, सी - आकृति का बड़ा पक्ष, ज्ञात डेटा के साथ एस - क्षेत्र, एन - मध्य रेखा, निम्नलिखित गणनाओं का उपयोग करें:

बी = एस/एन = 2एस/ (ए + के)

सी = एस/एन पाप α = 2एस/ (ए + के) पाप α

समद्विबाहु समलम्ब चतुर्भुज की भुजाएँ कैसे ज्ञात करें?

तो, एक समद्विबाहु समलंब के लिए, AB = DC। यदि आपको अलग-अलग मान दिए गए हैं, तो नीचे दिए गए सूत्रों का उपयोग करके भुजाएँ पाई जा सकती हैं:

• यदि ऊँचाई - h और कोण - α ज्ञात हो, तो AB = DC = h/sin α;
• यदि आधार और कोण का मान दिया गया है - α, तो AB = DC = (a - b)/ cos α;
• यदि विकर्ण d और आधार दिए गए हैं, तो AB² = DC² = d² - b a;
• यदि मान ज्ञात हैं मध्य रेखा- एल, क्षेत्र - एस, कोण - α या - β (आधार बी के पास शीर्ष पर, फिर एबी = डीसी = एस/ एल पाप α = एस/ एल पाप α।

एबी = डीसी = एस/ (बी + ए) पाप α = एस/ (बी + ए) पाप β

भविष्य में, यदि आप सूत्र सीखते हैं और इन आकृतियों के चित्र सही ढंग से बनाना सीखते हैं, तो ज्यामिति समस्या को हल करना आपके लिए मुश्किल नहीं होगा। आख़िरकार, सही तस्वीर के साथ, समस्या का उत्तर लगभग तुरंत दिखाई देता है।