यदि समद्विबाहु समलंब में विकर्ण लंबवत हैं, तो निम्नलिखित सैद्धांतिक सामग्री समस्या को हल करने में उपयोगी होगी।

1. यदि समद्विबाहु समलंब में विकर्ण लंबवत हैं, तो समलंब की ऊंचाई आधारों के योग के आधे के बराबर है।

आइए बिंदु C से होकर BD के समानांतर एक रेखा CF खींचें और रेखा AD को तब तक बढ़ाएं जब तक कि वह CF पर प्रतिच्छेद न कर दे।

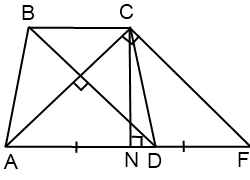
चतुर्भुज बीसीएफडी एक समांतर चतुर्भुज है (बीसी∥ डीएफ एक ट्रेपेज़ॉइड के आधार के रूप में, बीडी∥ सीएफ निर्माण के अनुसार)। तो CF=BD, DF=BC और AF=AD+BC।

त्रिभुज ACF समकोण है (यदि एक रेखा दो समानांतर रेखाओं में से एक पर लंबवत है, तो वह दूसरी रेखा पर भी लंबवत होती है)। चूँकि एक समद्विबाहु समलंब में विकर्ण बराबर होते हैं और CF=BD, तो CF=AC, अर्थात, त्रिभुज ACF आधार AF वाला समद्विबाहु है। इसका मतलब यह है कि इसकी ऊंचाई CN भी माध्यिका है। और चूँकि कर्ण पर खींचे गए समकोण त्रिभुज की माध्यिका उसके आधे के बराबर होती है, तो

क्या अंदर सामान्य रूप से देखेंके रूप में लिखा जा सकता है

जहां h समलम्ब चतुर्भुज की ऊंचाई है, a और b इसके आधार हैं।

2. यदि किसी समद्विबाहु समलंब में विकर्ण लंबवत हैं, तो इसकी ऊंचाई मध्य रेखा के बराबर होती है।

चूँकि समलम्ब चतुर्भुज m की मध्य रेखा आधारों के योग के आधे के बराबर है

3. यदि समद्विबाहु समलंब में विकर्ण लंबवत हैं, तो समलंब का क्षेत्रफल समलंब की ऊंचाई के वर्ग (या आधारों के आधे योग का वर्ग, या मध्य रेखा के वर्ग) के बराबर होता है ).

चूँकि समलम्ब चतुर्भुज का क्षेत्रफल सूत्र द्वारा ज्ञात किया जाता है

और ऊंचाई, आधारों का आधा योग और लंबवत विकर्णों के साथ एक समद्विबाहु समलंब की मध्य रेखा एक दूसरे के बराबर होती है:

ट्रेपेज़ॉइड है विशेष मामलाएक चतुर्भुज जिसकी भुजाओं का एक जोड़ा समानांतर हो। शब्द "ट्रेपेज़ॉइड" से आया है ग्रीक शब्दτράπεζα, जिसका अर्थ है "टेबल", "टेबल"। इस लेख में हम ट्रेपेज़ॉइड के प्रकार और उसके गुणों को देखेंगे। इसके अलावा, हम यह पता लगाएंगे कि इसके व्यक्तिगत तत्वों की गणना कैसे करें, उदाहरण के लिए, एक समद्विबाहु समलंब का विकर्ण, केंद्र रेखा, क्षेत्र, आदि। सामग्री को प्राथमिक लोकप्रिय ज्यामिति की शैली में प्रस्तुत किया गया है, अर्थात। आसानी से सुलभ रूप में .

सामान्य जानकारी

सबसे पहले, आइए जानें कि चतुर्भुज क्या है। यह आकृति चार भुजाओं और चार शीर्षों वाले बहुभुज का एक विशेष मामला है। चतुर्भुज के दो शीर्ष जो आसन्न नहीं हैं, विपरीत कहलाते हैं। यही बात दो गैर-आसन्न भुजाओं के बारे में भी कही जा सकती है। चतुर्भुज के मुख्य प्रकार समांतर चतुर्भुज, आयत, समचतुर्भुज, वर्ग, समलंब और डेल्टॉइड हैं।

तो चलिए ट्रैपेज़ॉइड्स पर वापस आते हैं। जैसा कि हम पहले ही कह चुके हैं, इस आकृति की दो समानांतर भुजाएँ हैं। इन्हें आधार कहा जाता है। अन्य दो (गैर-समानांतर) पार्श्व भुजाएँ हैं। परीक्षा सामग्री और विभिन्न में परीक्षणबहुत बार आपको ट्रेपेज़ॉइड से संबंधित समस्याएं मिल सकती हैं, जिनके समाधान के लिए अक्सर छात्र के पास उस ज्ञान की आवश्यकता होती है जो कार्यक्रम में प्रदान नहीं किया गया है। स्कूल ज्यामिति पाठ्यक्रम छात्रों को कोणों और विकर्णों के गुणों के साथ-साथ एक समद्विबाहु समलंब की मध्य रेखा से परिचित कराता है। लेकिन, इसके अतिरिक्त, उल्लिखित ज्यामितीय आकृति में अन्य विशेषताएं भी हैं। लेकिन उनके बारे में थोड़ा बाद में...

ट्रेपेज़ॉइड के प्रकार

यह आकृति कई प्रकार की होती है. हालाँकि, अक्सर उनमें से दो पर विचार करने की प्रथा है - समद्विबाहु और आयताकार।

1. एक आयताकार समलम्ब चतुर्भुज एक आकृति है जिसमें एक भुजा आधारों के लंबवत होती है। उसके दोनों कोण सदैव नब्बे डिग्री के बराबर होते हैं।

2. समद्विबाहु समलम्ब एक ज्यामितीय आकृति है जिसकी भुजाएँ एक दूसरे के बराबर होती हैं। इसका मतलब यह है कि आधारों पर बने कोण भी जोड़े में बराबर होते हैं।

ट्रैपेज़ॉइड के गुणों का अध्ययन करने की पद्धति के मुख्य सिद्धांत

मुख्य सिद्धांत में तथाकथित कार्य दृष्टिकोण का उपयोग शामिल है। वास्तव में, ज्यामिति के सैद्धांतिक पाठ्यक्रम में इस आकृति के नए गुणों को शामिल करने की कोई आवश्यकता नहीं है। उन्हें विभिन्न समस्याओं (अधिमानतः सिस्टम वाली) को हल करने की प्रक्रिया में खोजा और तैयार किया जा सकता है। साथ ही, यह बहुत महत्वपूर्ण है कि शिक्षक को पता हो कि शैक्षिक प्रक्रिया के दौरान किसी न किसी समय छात्रों को कौन से कार्य सौंपे जाने चाहिए। इसके अलावा, ट्रैपेज़ॉइड की प्रत्येक संपत्ति को कार्य प्रणाली में एक महत्वपूर्ण कार्य के रूप में दर्शाया जा सकता है।

दूसरा सिद्धांत ट्रेपेज़ॉइड के "उल्लेखनीय" गुणों के अध्ययन का तथाकथित सर्पिल संगठन है। इसका तात्पर्य सीखने की प्रक्रिया में किसी दिए गए व्यक्तिगत विशेषताओं की वापसी से है ज्यामितीय आकृति. इससे छात्रों को उन्हें याद रखना आसान हो जाता है। उदाहरण के लिए, चार बिंदुओं की संपत्ति. समानता का अध्ययन करते समय और बाद में वैक्टर का उपयोग करते समय इसे सिद्ध किया जा सकता है। और किसी आकृति की पार्श्व भुजाओं से सटे त्रिभुजों की समतुल्यता को न केवल एक ही सीधी रेखा पर स्थित भुजाओं पर समान ऊँचाई वाले त्रिभुजों के गुणों को लागू करके, बल्कि सूत्र S = 1/2( का उपयोग करके भी सिद्ध किया जा सकता है। अब*पाप)। इसके अलावा, आप एक खुदे हुए ट्रैपेज़ॉइड पर या एक खुदे हुए ट्रैपेज़ॉइड पर एक समकोण त्रिभुज आदि पर काम कर सकते हैं।

स्कूली पाठ्यक्रम की सामग्री में ज्यामितीय आकृति की "पाठ्येतर" विशेषताओं का उपयोग उन्हें पढ़ाने के लिए एक कार्य-आधारित तकनीक है। अन्य विषयों से गुजरते समय अध्ययन किए जा रहे गुणों का लगातार जिक्र करने से छात्रों को ट्रैपेज़ॉइड का गहरा ज्ञान प्राप्त करने की अनुमति मिलती है और निर्दिष्ट समस्याओं को हल करने की सफलता सुनिश्चित होती है। तो चलिए इस अद्भुत आंकड़े का अध्ययन शुरू करते हैं।

समद्विबाहु समलम्ब चतुर्भुज के तत्व और गुण

जैसा कि हम पहले ही नोट कर चुके हैं, इस ज्यामितीय आकृति की भुजाएँ समान हैं। इसे सही ट्रेपेज़ॉइड के रूप में भी जाना जाता है। यह इतना उल्लेखनीय क्यों है और इसे ऐसा नाम क्यों मिला? इस आकृति की ख़ासियत यह है कि न केवल आधार पर भुजाएँ और कोण समान हैं, बल्कि विकर्ण भी समान हैं। इसके अलावा, एक समद्विबाहु समलंब के कोणों का योग 360 डिग्री होता है। लेकिन वह सब नहीं है! सभी ज्ञात समलम्ब चतुर्भुजों में से केवल एक समद्विबाहु को एक वृत्त के रूप में वर्णित किया जा सकता है। यह इस तथ्य के कारण है कि इस आकृति के विपरीत कोणों का योग 180 डिग्री के बराबर है, और केवल इस स्थिति के तहत ही चतुर्भुज के चारों ओर एक वृत्त का वर्णन किया जा सकता है। विचाराधीन ज्यामितीय आकृति की अगली संपत्ति यह है कि आधार के शीर्ष से सीधी रेखा पर विपरीत शीर्ष के प्रक्षेपण तक की दूरी जिसमें यह आधार शामिल है, मध्य रेखा के बराबर होगी।

अब आइए जानें कि समद्विबाहु समलम्ब चतुर्भुज के कोण कैसे ज्ञात करें। आइए इस समस्या के समाधान पर विचार करें, बशर्ते कि आकृति की भुजाओं के आयाम ज्ञात हों।

समाधान

आमतौर पर, एक चतुर्भुज को आमतौर पर ए, बी, सी, डी अक्षरों द्वारा दर्शाया जाता है, जहां बीएस और एडी आधार हैं। एक समद्विबाहु समलंब में, भुजाएँ बराबर होती हैं। हम मान लेंगे कि उनका आकार X के बराबर है, और आधारों का आकार Y और Z (क्रमशः छोटा और बड़ा) के बराबर है। गणना करने के लिए, कोण बी से ऊंचाई एच खींचना आवश्यक है। परिणाम एक समकोण त्रिभुज एबीएन है, जहां एबी कर्ण है, और बीएन और एएन पैर हैं। हम पैर AN के आकार की गणना करते हैं: हम बड़े आधार से छोटे को घटाते हैं, और परिणाम को 2 से विभाजित करते हैं। हम इसे एक सूत्र के रूप में लिखते हैं: (Z-Y)/2 = F। अब, तीव्र की गणना करने के लिए त्रिभुज के कोण के लिए, हम कॉस फ़ंक्शन का उपयोग करते हैं। हमें निम्नलिखित प्रविष्टि मिलती है: cos(β) = X/F. अब हम कोण की गणना करते हैं: β=arcos (X/F)। इसके अलावा, एक कोण को जानकर, हम दूसरा निर्धारित कर सकते हैं, इसके लिए हम एक प्रारंभिक अंकगणितीय ऑपरेशन करते हैं: 180 - β। सभी कोण परिभाषित हैं.

इस समस्या का दूसरा समाधान भी है. सबसे पहले, हम इसे कोने से ऊंचाई एच तक कम करते हैं। हम पैर बीएन के मूल्य की गणना करते हैं। हम जानते हैं कि एक समकोण त्रिभुज के कर्ण का वर्ग पैरों के वर्गों के योग के बराबर होता है। हमें मिलता है: BN = √(X2-F2)। अगला हम उपयोग करते हैं त्रिकोणमितीय फलनटीजी. परिणामस्वरूप, हमारे पास है: β = आर्कटान (बीएन/एफ)। एक न्यून कोण पाया गया है. इसके बाद, हम पहली विधि की तरह ही अधिक कोण का निर्धारण करते हैं।

एक समद्विबाहु समलम्ब चतुर्भुज के विकर्णों की संपत्ति

सबसे पहले, आइए चार नियम लिखें। यदि एक समद्विबाहु समलंब में विकर्ण लंबवत हैं, तो:

आकृति की ऊंचाई दो से विभाजित आधारों के योग के बराबर होगी;

इसकी ऊंचाई और मध्य रेखा बराबर हैं;

वृत्त का केंद्र वह बिंदु है जिस पर;

यदि पार्श्व पक्ष को स्पर्शरेखा के बिंदु से खंड एच और एम में विभाजित किया गया है, तो यह बराबर है वर्गमूलइन खंडों के उत्पाद;

स्पर्शरेखा बिंदुओं, समलम्ब चतुर्भुज के शीर्ष और अंकित वृत्त के केंद्र से बनने वाला चतुर्भुज एक वर्ग होता है जिसकी भुजा त्रिज्या के बराबर होती है;

किसी आकृति का क्षेत्रफल आधारों के गुणनफल और आधारों के योग के आधे भाग और उसकी ऊँचाई के गुणनफल के बराबर होता है।

समान ट्रेपेज़ॉइड

यह विषय इसके गुणों का अध्ययन करने के लिए बहुत सुविधाजनक है। उदाहरण के लिए, विकर्ण एक समलंब को चार त्रिभुजों में विभाजित करते हैं, और जो आधार से सटे होते हैं वे समान होते हैं, और जो भुजाओं से सटे होते हैं उनका आकार समान होता है। इस कथन को उन त्रिभुजों का गुण कहा जा सकता है जिनमें समलम्ब चतुर्भुज को उसके विकर्णों द्वारा विभाजित किया जाता है। इस कथन का प्रथम भाग दो कोणों पर समानता के चिह्न से सिद्ध होता है। दूसरे भाग को सिद्ध करने के लिए नीचे दी गई विधि का उपयोग करना बेहतर है।

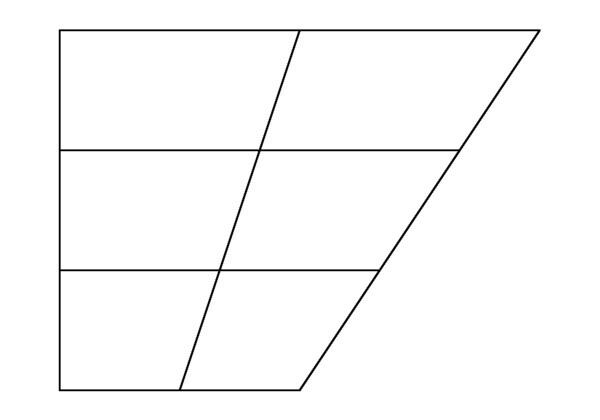
प्रमेय का प्रमाण

हम स्वीकार करते हैं कि आकृति ABSD (AD और BS समलम्ब चतुर्भुज के आधार हैं) को विकर्ण VD और AC द्वारा विभाजित किया गया है। उनके प्रतिच्छेदन का बिंदु O है। हमें चार त्रिकोण मिलते हैं: AOS - निचले आधार पर, BOS - ऊपरी आधार पर, ABO और SOD भुजाओं पर। यदि खंड BO और OD उनके आधार हैं तो त्रिभुज SOD और BOS की ऊँचाई समान है। हम पाते हैं कि उनके क्षेत्रों (पी) के बीच का अंतर इन खंडों के बीच के अंतर के बराबर है: पीबीओएस/पीएसओडी = बीओ/ओडी = के। इसलिए, पीएसओडी = पीबीओएस/के। इसी प्रकार, त्रिभुज BOS और AOB की ऊँचाई समान है। हम खंड CO और OA को उनके आधार के रूप में लेते हैं। हमें PBOS/PAOB = CO/OA = K और PAOB = PBOS/K मिलता है। इससे यह निष्कर्ष निकलता है कि PSOD = PAOB.

सामग्री को समेकित करने के लिए, छात्रों को निम्नलिखित समस्या को हल करके परिणामी त्रिभुजों के क्षेत्रों के बीच संबंध खोजने की सलाह दी जाती है जिसमें समलम्ब चतुर्भुज को उसके विकर्णों द्वारा विभाजित किया गया है। यह ज्ञात है कि त्रिभुज BOS और AOD का क्षेत्रफल समान है, समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात करना आवश्यक है। चूँकि PSOD = PAOB, इसका अर्थ है PABSD = PBOS+PAOD+2*PSOD। त्रिभुज BOS और AOD की समानता से यह निष्कर्ष निकलता है कि BO/OD = √(PBOS/PAOD)। इसलिए, पीबीओएस/पीएसओडी = बीओ/ओडी = √(पीबीओएस/पीएओडी)। हमें PSOD = √(PBOS*PAOD) मिलता है। तब PABSD = PBOS+PAOD+2*√(PBOS*PAOD) = (√PBOS+√PAOD)2.

समानता के गुण

इस विषय को विकसित करना जारी रखते हुए, कोई अन्य को साबित कर सकता है दिलचस्प विशेषताएंसमलम्बाकार। इस प्रकार, समानता का उपयोग करके, कोई उस खंड की संपत्ति को साबित कर सकता है जो आधारों के समानांतर, इस ज्यामितीय आकृति के विकर्णों के चौराहे से बने बिंदु से गुजरता है। ऐसा करने के लिए, आइए निम्नलिखित समस्या को हल करें: हमें बिंदु O से गुजरने वाले खंड RK की लंबाई ज्ञात करने की आवश्यकता है। त्रिकोण AOD और BOS की समानता से यह पता चलता है कि AO/OS = AD/BS। त्रिभुज AOP और ASB की समानता से यह निष्कर्ष निकलता है कि AO/AC=RO/BS=AD/(BS+AD)। यहां से हमें पता चलता है कि RO=BS*BP/(BS+BP)। इसी प्रकार, त्रिभुज DOC और DBS की समानता से यह निष्कर्ष निकलता है कि OK = BS*AD/(BS+AD)। यहां से हमें पता चलता है कि RO=OK और RK=2*BS*AD/(BS+AD)। आधारों के समानांतर और दो पार्श्व भुजाओं को जोड़ने वाले विकर्णों के प्रतिच्छेदन बिंदु से गुजरने वाला एक खंड, प्रतिच्छेदन बिंदु से आधे में विभाजित होता है। इसकी लंबाई आकृति के आधारों का हार्मोनिक माध्य है।

एक समलम्ब चतुर्भुज के निम्नलिखित गुण पर विचार करें, जिसे चार बिंदुओं का गुण कहा जाता है। विकर्णों (O) के प्रतिच्छेदन बिंदु, भुजाओं की निरंतरता का प्रतिच्छेदन (E), साथ ही आधारों (T और F) के मध्य बिंदु हमेशा एक ही रेखा पर स्थित होते हैं। इसे समानता विधि से आसानी से सिद्ध किया जा सकता है। परिणामी त्रिभुज BES और AED समान हैं, और उनमें से प्रत्येक में माध्यिकाएँ ET और EJ शीर्ष कोण E को समान भागों में विभाजित करती हैं। इसलिए, बिंदु E, T और F एक ही सीधी रेखा पर स्थित हैं। इसी प्रकार, बिंदु T, O, और Zh एक ही सीधी रेखा पर स्थित हैं। यह सब त्रिभुज BOS और AOD की समानता से होता है। यहां से हम यह निष्कर्ष निकालते हैं कि सभी चार बिंदु - ई, टी, ओ और एफ - एक ही सीधी रेखा पर स्थित होंगे।

समान ट्रेपेज़ॉइड का उपयोग करके, आप छात्रों से उस खंड (एलएस) की लंबाई खोजने के लिए कह सकते हैं जो आकृति को दो समान खंडों में विभाजित करता है। यह खंड आधारों के समानांतर होना चाहिए. चूँकि परिणामी समलम्बाकार ALFD और LBSF समान हैं, तो BS/LF = LF/AD। यह इस प्रकार है कि LF=√(BS*AD). हम पाते हैं कि समलम्ब चतुर्भुज को दो समान भागों में विभाजित करने वाले खंड की लंबाई आकृति के आधारों की लंबाई के ज्यामितीय माध्य के बराबर है।

चलो गौर करते हैं अगली संपत्तिसमानता यह एक खंड पर आधारित है जो समलंब को दो समान आकृतियों में विभाजित करता है। हम मानते हैं कि ट्रेपेज़ॉइड एबीएसडी को खंड ईएच द्वारा दो समान भागों में विभाजित किया गया है। शीर्ष B से एक ऊंचाई हटा दी जाती है, जिसे खंड EN द्वारा दो भागों - B1 और B2 में विभाजित किया जाता है। हमें मिलता है: PABSD/2 = (BS+EN)*B1/2 = (AD+EN)*B2/2 और PABSD = (BS+AD)*(B1+B2)/2। इसके बाद, हम एक सिस्टम बनाते हैं जिसका पहला समीकरण (BS+EN)*B1 = (AD+EN)*B2 और दूसरा (BS+EN)*B1 = (BS+AD)*(B1+B2)/2 है। यह इस प्रकार है कि B2/B1 = (BS+EN)/(AD+EN) और BS+EN = ((BS+AD)/2)*(1+B2/B1)। हम पाते हैं कि समलम्ब चतुर्भुज को दो बराबर भागों में विभाजित करने वाले खंड की लंबाई आधारों की लंबाई के मूल माध्य वर्ग के बराबर है: √((BS2+AD2)/2)।

समानता निष्कर्ष

इस प्रकार, हमने यह सिद्ध कर दिया है कि:

1. एक ट्रेपेज़ॉइड के पार्श्व पक्षों के मध्य बिंदुओं को जोड़ने वाला खंड AD और BS के समानांतर है और BS और AD के अंकगणितीय माध्य (ट्रेपेज़ॉइड के आधार की लंबाई) के बराबर है।

2. AD और BS के समानांतर विकर्णों के प्रतिच्छेदन के बिंदु O से गुजरने वाली रेखा संख्या AD और BS (2*BS*AD/(BS+AD)) के हार्मोनिक माध्य के बराबर होगी।

3. समलम्ब चतुर्भुज को समान भागों में विभाजित करने वाले खंड की लंबाई आधार बीएस और एडी के ज्यामितीय माध्य की होती है।

4. एक आकृति को दो बराबर भागों में विभाजित करने वाले तत्व की लंबाई AD और BS संख्याओं के मूल माध्य वर्ग की होती है।

सामग्री को समेकित करने और विचारित खंडों के बीच संबंध को समझने के लिए, छात्र को उन्हें एक विशिष्ट ट्रेपोज़ॉइड के लिए बनाने की आवश्यकता है। वह आसानी से मध्य रेखा और उस खंड को प्रदर्शित कर सकता है जो बिंदु O से होकर गुजरता है - आकृति के विकर्णों का प्रतिच्छेदन - आधारों के समानांतर। लेकिन तीसरा और चौथा कहाँ स्थित होगा? यह उत्तर छात्र को औसत मूल्यों के बीच वांछित संबंध की खोज की ओर ले जाएगा।

समलम्ब चतुर्भुज के विकर्णों के मध्यबिंदुओं को जोड़ने वाला एक खंड

इस आकृति की निम्नलिखित संपत्ति पर विचार करें। हम मानते हैं कि खंड MH आधारों के समानांतर है और विकर्णों को समद्विभाजित करता है। आइए प्रतिच्छेदन बिंदुओं को Ш और Ш कहते हैं। यह खंड आधारों के आधे अंतर के बराबर होगा। आइए इसे और अधिक विस्तार से देखें। MS, ABS त्रिभुज की मध्य रेखा है, यह BS/2 के बराबर है। MSH त्रिभुज ABD की मध्य रेखा है, यह AD/2 के बराबर है। तब हम पाते हैं कि ShShch = MSh-MSh, इसलिए, ShShch = AD/2-BS/2 = (AD+VS)/2।

ग्रैविटी केंद्र

आइए देखें कि किसी दिए गए ज्यामितीय आकृति के लिए यह तत्व कैसे निर्धारित किया जाता है। ऐसा करने के लिए, मैदान को अंदर तक विस्तारित करना आवश्यक है विपरीत दिशाएं. इसका मतलब क्या है? आपको निचले आधार को ऊपरी आधार से जोड़ने की आवश्यकता है - किसी भी दिशा में, उदाहरण के लिए, दाईं ओर। और हम निचले हिस्से को ऊपरी हिस्से की लंबाई से बाईं ओर बढ़ाते हैं। अगला, हम उन्हें तिरछे जोड़ते हैं। आकृति की मध्य रेखा के साथ इस खंड का प्रतिच्छेदन बिंदु समलम्ब चतुर्भुज का गुरुत्वाकर्षण केंद्र है।

उत्कीर्ण और परिचालित समलम्बाकार

आइए ऐसी आकृतियों की विशेषताएं सूचीबद्ध करें:

1. एक समलम्ब चतुर्भुज को एक वृत्त में तभी अंकित किया जा सकता है जब वह समद्विबाहु हो।

2. एक समलंब को एक वृत्त के चारों ओर वर्णित किया जा सकता है, बशर्ते कि उनके आधारों की लंबाई का योग भुजाओं की लंबाई के योग के बराबर हो।

अंतःवृत्त के परिणाम:

1. वर्णित ट्रेपेज़ॉइड की ऊंचाई हमेशा दो त्रिज्याओं के बराबर होती है।

2. वर्णित समलम्ब चतुर्भुज का किनारा वृत्त के केंद्र से समकोण पर देखा जाता है।

पहला परिणाम स्पष्ट है, लेकिन दूसरे को साबित करने के लिए यह स्थापित करना आवश्यक है कि कोण एसओडी सही है, जो वास्तव में मुश्किल भी नहीं है। लेकिन इस संपत्ति का ज्ञान आपको समस्याओं को हल करते समय एक समकोण त्रिभुज का उपयोग करने की अनुमति देगा।

आइए अब हम एक वृत्त में अंकित समद्विबाहु समलम्ब चतुर्भुज के लिए इन परिणामों को निर्दिष्ट करें। हम पाते हैं कि ऊँचाई आकृति के आधारों का ज्यामितीय माध्य है: H=2R=√(BS*AD)। समलम्ब चतुर्भुज (दो ऊँचाइयाँ खींचने का सिद्धांत) की समस्याओं को हल करने की बुनियादी तकनीक का अभ्यास करते समय, छात्र को निम्नलिखित कार्य को हल करना होगा। हम मानते हैं कि BT समद्विबाहु आकृति ABSD की ऊंचाई है। एटी और टीडी खंडों को खोजना आवश्यक है। ऊपर वर्णित सूत्र का उपयोग करके ऐसा करना कठिन नहीं होगा।

अब आइए जानें कि परिचालित समलम्ब चतुर्भुज के क्षेत्रफल का उपयोग करके किसी वृत्त की त्रिज्या कैसे निर्धारित की जाए। हम शीर्ष B से आधार AD तक ऊँचाई कम करते हैं। चूँकि वृत्त एक समलम्ब चतुर्भुज में अंकित है, तो BS+AD = 2AB या AB = (BS+AD)/2. त्रिभुज ABN से हम पाते हैं कि synα = BN/AB = 2*BN/(BS+AD)। पीएबीएसडी = (बीएस+बीपी)*बीएन/2, बीएन=2आर। हमें PABSD = (BS+BP)*R मिलता है, यह इस प्रकार है कि R = PABSD/(BS+BP)।

.

समलम्ब चतुर्भुज की मध्य रेखा के लिए सभी सूत्र

अब इस ज्यामितीय आकृति के अंतिम तत्व पर आगे बढ़ने का समय आ गया है। आइए जानें कि समलम्ब चतुर्भुज (M) की मध्य रेखा किसके बराबर है:

1. आधारों के माध्यम से: एम = (ए+बी)/2.

2. ऊंचाई, आधार और कोनों के माध्यम से:

एम = ए-एच*(ctgα+ctgβ)/2;

एम = बी+एन*(ctgα+ctgβ)/2.

3. ऊंचाई, विकर्ण और उनके बीच का कोण। उदाहरण के लिए, D1 और D2 एक समलम्ब चतुर्भुज के विकर्ण हैं; α, β - उनके बीच के कोण:

एम = D1*D2*sinα/2Н = D1*D2*sinβ/2Н।

4. क्षेत्रफल और ऊंचाई के माध्यम से: एम = पी/एन।

इससे पहले कि हम यह समझें कि समलम्ब चतुर्भुज का विकर्ण कैसे ज्ञात किया जाए, आइए याद रखें कि समलम्ब चतुर्भुज क्या है। प्लैनिमेट्री में, ट्रैपेज़ॉइड एक चतुर्भुज है जिसकी दो विपरीत भुजाएँ एक दूसरे के समानांतर होती हैं। इन समानांतर भुजाओं को समलम्ब चतुर्भुज का आधार कहा जाता है, और शेष को पार्श्व भुजाएँ कहा जाता है। भुजाएँ समान हो सकती हैं, तो हम एक समद्विबाहु समलंब के साथ काम कर रहे हैं।

इसके बाद, हम सामान्य मामले - एक समद्विबाहु समलंब के लिए विकर्णों की लंबाई ज्ञात करने की प्रक्रिया का विस्तार से विश्लेषण करेंगे। इस मामले में, हम इस तथ्य से आगे बढ़ेंगे कि प्रारंभिक डेटा ट्रेपेज़ॉइड के सभी चार पक्षों की लंबाई है, आधार पर कोण अज्ञात हैं।

समलम्ब चतुर्भुज के विकर्ण की गणना

चित्र में दिखाए गए समलम्ब चतुर्भुज ABCD के दो विकर्ण AC और BD हैं। उनकी लंबाई ज्ञात करने का क्रम समान है, तो आइए ˂BAD के विपरीत विकर्ण BD खोजने के उदाहरण का उपयोग करके सब कुछ पर विचार करें।

विकर्ण BD भी त्रिभुज ABD की एक भुजा है और सूत्र का उपयोग करके कोज्या के नियम का उपयोग करके इसकी गणना की जा सकती है:

BD = √(AB 2 +AD 2 -2AB . AD . cos ˂BAD)

इस सूत्र में हम कोज्या ˂BAD को छोड़कर सभी मात्राएँ जानते हैं। इसकी गणना करने के लिए, हमें ड्राइंग पर एक छोटा सा परिवर्तन करने की आवश्यकता होगी। आइए मूल ट्रैपेज़ॉइड से एक बीएनएमसी आयत को "काटें"। परिणामस्वरूप, हमें एक त्रिभुज ABD" प्राप्त होता है, जिसमें भुजा BD" समलम्ब चतुर्भुज CD की भुजा के बराबर होगी।

एक त्रिभुज में ˂BAD" एक समलम्ब चतुर्भुज में ˂BAD के बराबर है, क्योंकि हमने त्रिभुज ABN के साथ कोई परिवर्तन नहीं किया है। इसलिए, इस त्रिभुज में ABD" भुजा AB हमें ज्ञात है, भुजा BD" = CD, और भुजा AD" = एडी - एनएम = एडी - बी.सी.

यह पता चलता है कि कोसाइन प्रमेय से cos ˂BAD = cos ˂BAD" = (AB 2 + AD" 2 - BD" 2)/2AB. AD" = (AB 2 + (AD - BC) 2 - CD 2)/ 2AB. (एडी-बीसी)

अब परिणामी अभिव्यक्ति को पहले पाए गए सूत्र में प्रतिस्थापित करने पर, हमें मिलता है:

BD = √(AB 2 +AD 2 -2AB . AD . cos ˂BAD) = √(AB 2 +AD 2 -2AB . AD . (AB 2 +(AD – BC) 2 – CD 2)/2AB . (AD – BC)) = √(AB 2 + AD 2 – AD. (AB 2 +(AD – BC) 2 – CD 2)/(AD – BC)) = √(AB 2 + AD 2 – AD. (AD – BC) 2 /(AD – BC) – AD . (AB 2 – CD 2)/(AD – BC)) = √(AB 2 + AD 2 – AD 2 + AD . BC – AD . (AB 2 – CD 2) )/(AD - BC)) = √(AB 2 + AD . BC - AD . (AB 2 - CD 2)/(AD - BC))

बीडी = √(एबी 2 + एडी । बीसी - एडी । (एबी 2 - सीडी 2)/(एडी - बीसी))

समलम्ब चतुर्भुज के विकर्ण का परिणामी सूत्र मूल चतुर्भुज की भुजाओं की लंबाई के किसी भी मान के लिए मान्य है।

दूसरे विकर्ण के लिए, सूत्र तदनुसार रूप लेगा:

एसी = √(सीडी 2 + एडी . बीसी - एडी . (सीडी 2 - एबी 2)/(एडी - बीसी))

एक समद्विबाहु समलंब चतुर्भुज का विकर्ण

यदि आप इस बात में रुचि रखते हैं कि समद्विबाहु समलम्ब चतुर्भुज का विकर्ण कैसे ज्ञात किया जाए, तो परिणामी सूत्र को बहुत सरल बनाया जा सकता है। वास्तव में, एक समद्विबाहु समलम्ब चतुर्भुज AB = CD में, इसलिए AB 2 - CD 2 = 0 और विकर्ण की लंबाई का सूत्र इस रूप में घटाया गया है:

बीडी = √(एबी 2 + एडी बीसी)

एक समद्विबाहु समलम्ब चतुर्भुज के विकर्ण एक दूसरे के बराबर होते हैं, इसलिए दूसरा विकर्ण उसी सूत्र का उपयोग करके पाया जाता है।

यदि प्रारंभिक डेटा ट्रेपेज़ॉइड के आधारों की लंबाई, पार्श्व पक्षों में से एक और आधार पर कोण हैं, तो ट्रेपेज़ॉइड के विकर्ण को खोजने का कार्य कोसाइन प्रमेय का उपयोग करके त्रिकोण के किनारे की गणना करने के लिए कम हो जाता है।

(प्राचीन ग्रीक τραπέζιον से - "टेबल"; τράπεζα - "टेबल, भोजन") - एक चतुर्भुज जिसमें विपरीत भुजाओं का केवल एक जोड़ा समानांतर होता है।

कभी-कभी एक ट्रेपेज़ॉइड को एक चतुर्भुज के रूप में परिभाषित किया जाता है जिसमें विपरीत भुजाओं का एक जोड़ा समानांतर होता है (अन्य निर्दिष्ट नहीं है), इस मामले में यह एक ट्रेपेज़ॉइड का एक विशेष मामला है। विशेष रूप से, एक वक्ररेखीय समलम्बाकार की अवधारणा है।

ट्रेपेज़ॉइड तत्व

• समानांतर भुजाएँकहा जाता है कारणसमलम्ब चतुर्भुज।
• बाकी दो पक्षों को बुलाया जाता है दोनों पक्ष.
• पार्श्व भुजाओं के मध्यबिंदुओं को जोड़ना कहलाता है मध्य रेखासमलम्ब चतुर्भुज।
• आधारों के बीच की दूरी कहलाती है ऊंचाईसमलम्ब चतुर्भुज।

ट्रेपेज़ॉइड के प्रकार

• वह समलम्ब चतुर्भुज जिसकी भुजाएँ बराबर हों, कहलाता है समद्विबाहु.
• एक समलम्ब चतुर्भुज जिसमें एक कोण "सीधा" होता है, कहलाता है आयताकार.

सामान्य विशेषता

• समलम्ब चतुर्भुज की मध्य रेखा आधारों के समानांतर और उनके आधे योग के बराबर है।
• विकर्णों के मध्यबिंदुओं को जोड़ने वाला खंड आधारों के अंतर के आधे के बराबर है।
• (सामान्यीकृत थेल्स)। किसी कोण की भुजाओं को प्रतिच्छेद करने वाली समानांतर रेखाएँ कोण की भुजाओं से आनुपातिक खंडों को काट देती हैं।

एक समद्विबाहु समलम्ब चतुर्भुज के गुण

• , आधारों के मध्य बिंदुओं से गुजरते हुए, आधारों के लंबवत है और समलम्ब चतुर्भुज की समरूपता की धुरी है।
• शीर्ष से बड़े आधार तक कम की गई ऊँचाई इसे दो खंडों में विभाजित करती है, जिनमें से एक आधारों के योग के आधे के बराबर है, दूसरा - आधारों के अंतर का आधा।
• समद्विबाहु समलम्ब चतुर्भुज में, किसी भी आधार पर कोण बराबर होते हैं।
• एक समद्विबाहु समलम्ब चतुर्भुज में, विकर्णों की लंबाई बराबर होती है।
• एक समद्विबाहु समलम्बाकार के बारे में वर्णित किया जा सकता है।
• यदि समद्विबाहु समलंब में विकर्ण लंबवत हैं, तो ऊंचाई आधारों के योग के आधे के बराबर है,

वह चतुर्भुज जिसमें केवल दो भुजाएँ समान्तर हों, कहलाता है चतुर्भुज.

किसी समलम्ब चतुर्भुज की समानांतर भुजाएँ उसकी कहलाती हैं कारण, और वे भुजाएँ जो समानांतर नहीं हैं, कहलाती हैं दोनों पक्ष. यदि भुजाएँ समान हों, तो ऐसा समलम्ब चतुर्भुज समद्विबाहु होता है। आधारों के बीच की दूरी को समलम्ब चतुर्भुज की ऊँचाई कहा जाता है।

मध्य रेखा समलम्ब चतुर्भुज

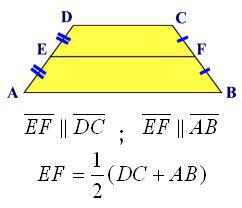
मध्य रेखा ट्रेपेज़ॉइड के पार्श्व पक्षों के मध्य बिंदुओं को जोड़ने वाला एक खंड है। समलम्ब चतुर्भुज की मध्य रेखा इसके आधारों के समानांतर होती है।

प्रमेय:

यदि एक सीधी रेखा एक भुजा के मध्य को काटती हुई समलम्ब चतुर्भुज के आधारों के समानांतर है, तो यह दूसरी भुजा को समद्विभाजित करती है ओरसमलम्ब चतुर्भुज।

प्रमेय:

मध्य रेखा की लंबाई उसके आधारों की लंबाई के अंकगणितीय माध्य के बराबर होती है

एमएन मध्य रेखा, एबी और सीडी - आधार, एडी और बीसी - पार्श्व पक्ष

एमएन = (एबी + डीसी)/2

प्रमेय:

एक समलम्ब चतुर्भुज की मध्य रेखा की लंबाई उसके आधारों की लंबाई के अंकगणितीय माध्य के बराबर होती है।

मुख्य कार्य: सिद्ध करें कि एक समलम्ब चतुर्भुज की मध्य रेखा एक खंड को समद्विभाजित करती है जिसके सिरे समलम्ब चतुर्भुज के आधारों के मध्य में स्थित होते हैं।

त्रिभुज की मध्य रेखा

किसी त्रिभुज की दो भुजाओं के मध्यबिंदुओं को जोड़ने वाला खंड त्रिभुज की मध्य रेखा कहलाता है। यह तीसरी भुजा के समानांतर है और इसकी लंबाई तीसरी भुजा की आधी लंबाई के बराबर है।
प्रमेय: यदि किसी त्रिभुज की एक भुजा के मध्यबिंदु को प्रतिच्छेद करने वाली रेखा त्रिभुज की दूसरी भुजा के समानांतर हो, तो वह तीसरी भुजा को समद्विभाजित करती है।

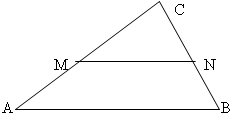
एएम = एमसी और बीएन = एनसी =>

एक त्रिभुज और समलम्ब चतुर्भुज की मध्य रेखा गुणों को लागू करना

किसी खंड को निश्चित संख्या में बराबर भागों में बाँटना।
कार्य: खंड AB को 5 बराबर भागों में विभाजित करें।
समाधान:
मान लीजिए p एक यादृच्छिक किरण है जिसका मूल बिंदु A है और जो रेखा AB पर स्थित नहीं है। हम क्रमिक रूप से पी एए 1 = ए 1 ए 2 = ए 2 ए 3 = ए 3 ए 4 = ए 4 ​​ए 5 पर 5 समान खंड अलग रखते हैं।
हम A 5 को B से जोड़ते हैं और A 4, A 3, A 2 और A 1 से होकर ऐसी रेखाएँ खींचते हैं जो A 5 B के समानांतर हैं। वे AB को क्रमशः बिंदु B 4, B 3, B 2 और B 1 पर काटते हैं। ये बिंदु खंड AB को 5 बराबर भागों में विभाजित करते हैं। दरअसल, समलम्ब चतुर्भुज BB 3 A 3 A 5 से हम देखते हैं कि BB 4 = B 4 B 3. इसी प्रकार, समलम्ब चतुर्भुज B 4 B 2 A 2 A 4 से हमें B 4 B 3 = B 3 B 2 प्राप्त होता है।

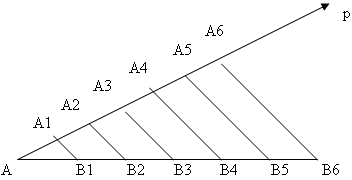
जबकि समलंब से B 3 B 1 A 1 A 3, B 3 B 2 = B 2 B 1.
फिर बी 2 एए 2 से यह निष्कर्ष निकलता है कि बी 2 बी 1 = बी 1 ए। निष्कर्ष में हम पाते हैं:
एबी 1 = बी 1 बी 2 = बी 2 बी 3 = बी 3 बी 4 = बी 4 बी
यह स्पष्ट है कि खंड AB को अन्य समान भागों में विभाजित करने के लिए, हमें समान संख्या में समान खंडों को किरण p पर प्रक्षेपित करने की आवश्यकता है। और फिर ऊपर वर्णित तरीके से जारी रखें।