Діаметр описаного кола трикутника. Конспект уроку "описане коло". Як знайти радіус кола, описаного біля трикутника - загальна формула
У цій частині ми обговоримо коло, описане навколо (часто кажуть «біля») трикутника. Насамперед дамо визначення.
1. Існування та центр описаного кола
Тут виникає запитання: а чи для будь-якого трикутника існує таке коло? Ось виявляється, що так, для кожного. Більше того, ми зараз сформулюємо теорему, яка ще й відповідає на питання, де ж знаходиться центр описаного кола.
Формули для знаходження довжини діагоналі прямокутника
Формула на стороні прямокутника по діаметру та куту β. Він називається діагоналлю прямокутника для будь-якого сегмента, що з'єднує дві вершини протилежних кутів прямокутника. Формула діагоналі прямокутника через дві сторони прямокутника.
Формула діагоналі прямокутника за площею та з обох сторін. Формула діагоналі прямокутника по периметру та з обох боків. Формула діагоналі прямокутника через радіус описаного кола. Формула діагоналі прямокутника по колу кола.
Дивись, ось так:
Давай наберемося мужності та доведемо цю теорему. Якщо ти читав уже тему « » розбирався в тому, чому три бісектриси перетинаються в одній точці, то тобі буде легше, але і якщо не читав - не переживай: зараз у всьому розберемося.
Доказ проводитимемо, використовуючи поняття геометричного місця точок (ГМТ).
Формула діагоналі прямокутника через синус кута, що прилягає до діагоналі, та довжину сторони, протилежну цьому куту. Формула діагоналі прямокутника через косинус кута, що прилягає до діагоналі, і довжину сторони, що прилягає до цього кута. Формула діагоналі прямокутника через синус гострого кута між діагоналями та площею прямокутника.
Формули визначення довжини периметра прямокутника
Периметр прямокутника називається сумою довжин усіх сторін прямокутника. Формула периметра прямокутника через дві сторони прямокутника. Формула периметра прямокутника за площею та з обох сторін. Формула периметра прямокутника по діагоналі та з обох сторін.
Ну от, наприклад, чи є безліч м'ячів – геометричним місцем круглих предметів? Ні, звичайно, тому що бувають круглі кавуни. А чи є безліч людей, «геометричним місцем», які вміють говорити? Теж ні, бо є немовлята, які не вміють говорити. У житті взагалі складно знайти приклад справжнього геометричного місця точок. У геометрії простіше. Ось, наприклад, саме те, що нам потрібно:
Формула периметра прямокутника через радіус описаного кола та з обох сторін. Формула периметра прямокутника по діаметру описаного кола та з обох сторін. Він називається площею прямокутника у просторі, обмеженому сторонами прямокутника, тобто усередині області периметра прямокутника.
Формули для визначення області прямокутника
Формула площі прямокутника із двох сторін. Формула площі прямокутника по периметру та з обох сторін. Формула площі прямокутника по діагоналі та з обох сторін. Формула площі прямокутника по діагоналі та синус гострого кута між діагоналями.
Тут безліч - це серединний перпендикуляр, а властивість "" - це "бути рівновіддаленою (точкою) від кінців відрізка".
Перевіримо? Отже, потрібно впевнитись у двох речах:
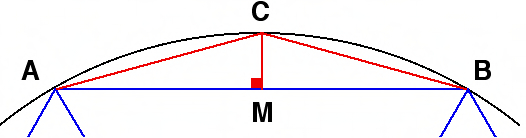
З'єднаємо з і с. Тоді лінія є медіаною та висотою ст. Значить, рівнобедрений, переконалися, що будь-яка точка, що лежить на серединному перпендикулярі, однаково віддалена від точок і.
Окружність, обмежена навколо прямокутника
Формула площі прямокутника по радіусу описаного кола та будь-якої сторони. Формула площі прямокутника по колу кола кола та з обох сторін. Він називається колом, обмеженим навколо прямокутника, до кола, що проходить через чотири вершини прямокутника, центром якого є перетин діагоналей прямокутника.
Формули для знаходження радіуса кола, описаного навколо прямокутника
Формула радіуса кола обмежена прямокутником через дві сторони. Формула радіуса кола описана навколо прямокутника по периметру квадрата і будь-якої зі сторін. Формула радіуса кола описана навколо прямокутника через площу прямокутника і довжину однієї з її сторін.
Візьмемо – середину і з'єднаємо в. Вийшла медіана. Але – рівнобедрений за умовою не лише медіана, а й висота, тобто – серединний перпендикуляр. Значить, точка – точно лежить на серединному перпендикулярі.
Всі! Повністю перевірили те що, що серединний перпендикуляр до відрізка є геометричним місцем точок, рівновіддалених від кінців відрізка.
Формула радіуса кола описана навколо прямокутника по діагоналі прямокутника. Формула радіуса кола, описана навколо прямокутника по окружному діаметру кола. Формула радіуса кола, описана навколо прямокутника через синус кута, що прилягає до діагоналі, і довжину сторони, протилежну цьому куту.
Колом, що оточує даний багатокутник, є описане коло. Більшість людей чули терміни коло та радіус, але обмежене коло - менш знайомий термін. Уявіть багатокутник двовимірної форми з прямими сторонами, як трикутник. Уявіть собі коло навколо трикутника, щоб він торкався всіх трьох його вершин; це обмежене коло. Щоб обчислити свій радіус, просто використовуйте просту алгебру та калькулятор.
Це все добре, але чи не забули ми про описане коло? Зовсім ні, ми якраз підготували собі «плацдарм для нападу».
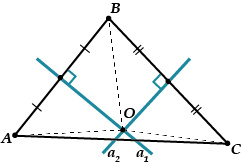
Розглянемо трикутник. Проведемо два серединні перпендикуляри і, скажімо, до відрізків і. Вони перетнуться в якійсь точці, яку ми назвемо.
Перевірте всі ваші вимірювання і переконайтеся, що компас говорить не змінюється, поки ви кружляли.
- Надзвичайно важливо точно та точно виміряти.
- Не всі полігони можуть мати обмежене коло.
Отже, площа кола, вписаного шестикутник, дорівнює. Тепер переходимо до вписаного квадрата. Оскільки діагональ квадрата дорівнює стороні кореневих часів, ми маємо. Тоді радіус кола, вписаного у квадрат, матиме половину міри сторони. Таким чином, ви побачите, що радіус кола, вписаного в трикутник, становить половину радіуса кола, описаного в трикутнику, оскільки коло кола описується розділеним середовищем на дві частини, пропорційні 1, а потім радіус вписаного кола буде.
А тепер, увага!
Крапка лежить на серединному перпендикулярі;
точка лежить на серединному перпендикулярі.
Отже, в.
Звідси випливає відразу кілька речей:
По перше, точка повинна лежати третьому серединному перпендикулярі, до відрізку.
Вимірювання кола та наближення
Таким чином, площа вписаного кола буде. І проблема полягає в тому, щоб довести, що сума цих площ дорівнює площі внутрішнього кола. Отже, зробіть суму областей коронок. Це сума площ коронок. Вам видно, що у нас є 3 кола променів. У цій статті пропонується гіпотеза, привід для розгляду деяких пунктів математики цього періоду в Месопотамії.
Утворюючи коло між двома шестикутниками, периметр яких легко підраховується, потім послідовно подвоюючи кількість сторін, він отримує багатокутники з 96 сторонами раму. Ймовірно, легше оцінити продуктивність, вказавши числові значення.
Тобто серединний перпендикуляр теж повинен пройти через точку, і всі три серединні перпендикуляри перетнулися в одній точці.
По-друге: якщо ми проведемо коло з центром у точці і радіусом, то це коло також пройде і через точку, і через точку, тобто буде описаним колом. Отже, вже є, що перетин трьох перпендикулярів – центр описаного кола для будь-якого трикутника.
Ми бачимо тут інтерес та ефективність методів спостереження: з одного боку, вони забезпечують наближення, з другого боку, дозволяють контролювати досконалу помилку. Наскільки мені відомо, Архімед першим явно обґрунтовує свої результати щодо кола і дає крок за кроком низку аргументів, які пояснюють, чому те, що він стверджує, є істинним. Але він не перший, хто цікавиться навколо та його мірою. У нас є дуже давні свідчення, один у Єгипті та деякі інші в Месопотамії, що йдуть у цьому напрямі.
І є деякі «вавилонські» глиняні таблички, що належать до того ж періоду і по периметру чи площі диска. Це предмет цієї статті. Прогулянка може початися, але перед від'їздом до Вавилону 17 або 18 століть до нашої ери. Було знайдено вавілонську пігулку з глини, яка дає відношення периметра шестикутника до периметру його обмеженого кола.
І останнє: про єдиність. Ясно (майже), що точку можна отримати єдиним чином, тому й коло – єдине. Ну, а "майже" - залишимо на твоє роздуми. Ось і довели теорему. Можна кричати "Ура!".
А якщо в задачі стоїть питання «знайдіть радіус описаного кола»? Або навпаки, радіус дано, а потрібно знайти щось інше? Чи є формула, що зв'язує радіус описаного кола з іншими елементами трикутника?
І вони часто додають у тій чи іншій формі. Це було другим, що викликало в мене проблему: чи могли вавилоняни справді знайти це значення експериментально? В даний час досвід простий у використанні, з метром швачки та повсякденними предметами різного діаметру: сковорода, каструля, бляшанки. Вимірюється периметр та діаметр, і проводиться поділ. Відмінності були у третьому знаку після коми. Звичайно, немає таких точних промислових предметів, ні метрів швачки, градуйованих у міліметрах.
Для виміру він тонший: мотузка, шкіряний ремінець, можуть розтягуватися під напругою і укладати контракт у спокої. З іншого боку, висушена кора папірусу не подовжується. На жаль, я його не мав. Очевидно, що вони не градуйовані, але це несерйозно: нас цікавить співвідношення двох довжин: від периметра та діаметра, а не від самих довжин. Легко обійти об'єкт із ротаном та розрізати його. Цікаво, що менш легко точно відрізати нитку ротанга, відповідну діаметру. Справді, верхній край кераміки часто заокруглюється.
Найчастіше під час вирішення геометричних завдань доводиться робити події з допоміжними постатями. Наприклад, знаходити радіус вписаного або описаного кола тощо. Ця стаття покаже, як знаходити радіус кола, описаного біля трикутника. Або, іншими словами, радіус кола, в яке вписано трикутник.
Тому необхідно виправити ротанг по периметру, а потім розрізати другий ротанг-ніж, що відповідає внутрішньому діаметру першого. Залишається розрахувати співвідношення двох довжин, не знаючи їх точних значеньЩо можна зробити, повернувшись до самого походження поділу. 
Моя найкраща продуктивність була у 6, 8 разів, тобто 6 разів, із чудовим відпочинком. Тим не менш, ці експерименти переконали мене, що вавилоняни не отримали експериментальної цінності, принаймні не від цього шлях. Але в цьому випадку виникають два питання.
Як знайти радіус кола, описаного біля трикутника - загальна формула
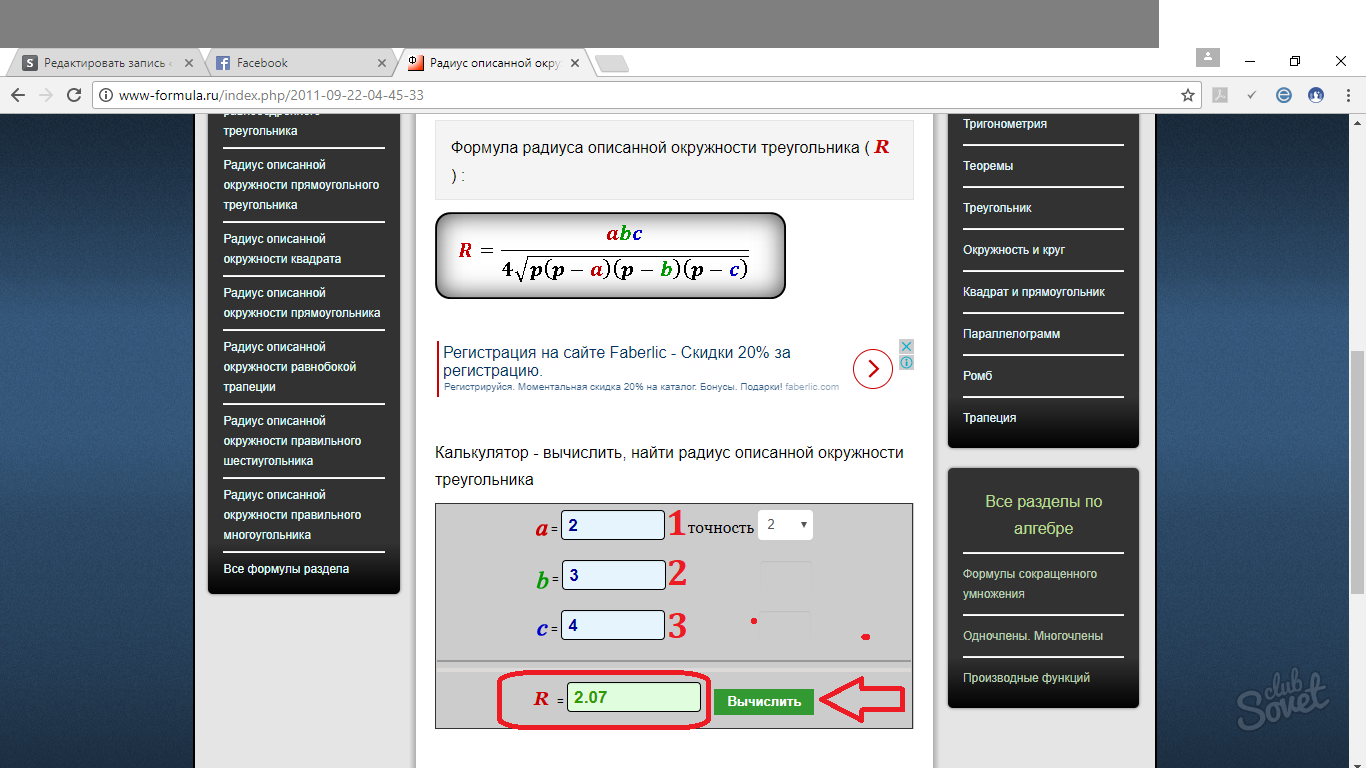
Загальна формула виглядає наступним чином: R = abc/4√p(p - a) (p - b) (p - c), де R - радіус описаного кола, p - периметр трикутника поділений на 2 (напівпериметр). a, b, c - Сторони трикутника.
Знайти радіус описаного кола трикутника, якщо a = 3, b = 6, c = 7.
Запитання 1: Якщо він не є експериментальним, він теоретичний, геометричний. 
Таким чином, периметр Р кола більше, ніж у шестикутника, і співвідношення між ними дорівнює. Для нас цілком природно оцінити периметр кола, невідомий стосовно того, що відомо самому шестикутнику.
Пізніше ми побачимо, що думати про це. Гіпотеза 1: Вавилонці знали теорему Піфагора за тисячу років до цього. Гіпотеза 2 вони знали, що знайшли прямокутники цілих сторін. Можливо, не всі, але принаймні ті, чия гіпотенуза і одна зі сторін є цілими цілими числами.
Таким чином, виходячи з наведеної вище формули, обчислюємо напівпериметр:
p = (a + b + c) / 2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Підставляємо значення формулу і отримуємо:
R = 3×6×7/4√8(8 — 3)(8 — 6)(8 — 7) = 126/4√(8×5×2×1) = 126/4√80 = 126/16 √5.
Відповідь: R = 126/16√5
Як знайти радіус кола, описаного біля рівностороннього трикутника
Для знаходження радіуса кола, описаного біля рівностороннього трикутника, є досить проста формула: R = a/√3, де a — величина його сторони.
Зрозуміло, немає жодних доказів того, що вавилоняни це зробили. Лише відкриття нової глиняної пігулки може зробити це. Більше того, ця ідея ґрунтується на гіпотезах 1 і чи справді вавилоняни знали, як знайти такі трикутники? 
Останні 15 рядків поділено на 4 стовпці, перші два рядки яких визначають вміст. Стовпець 4 містить знак, за яким йдуть цифри від 1 до.
Приклад: Сторона рівностороннього трикутника дорівнює 5. Знайти радіус описаного кола.
Так як у рівностороннього трикутника всі сторони рівні, для вирішення завдання потрібно лише вписати її значення у формулу. Отримаємо: R = 5/3.
Відповідь: R = 5/√3.
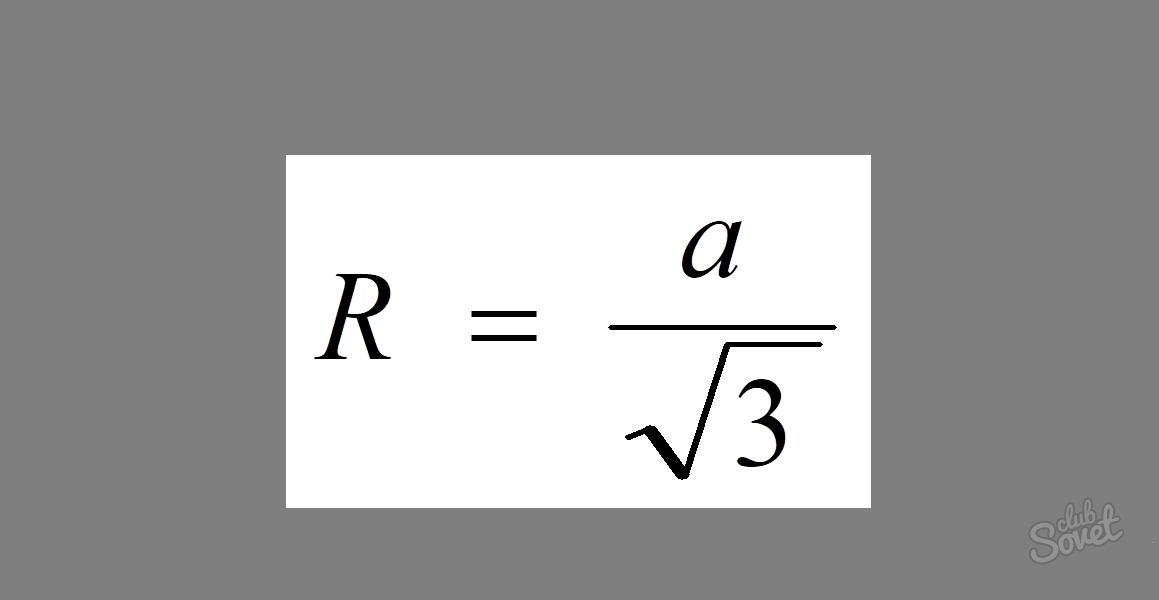
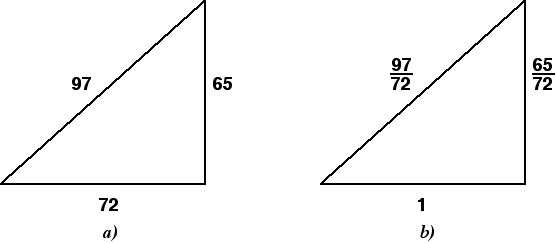
Як знайти радіус кола, описаного біля прямокутного трикутника
Формула виглядає так: R = 1/2 × √(a² + b²) = c/2, де a і b — катети і c — гіпотенуза. Якщо скласти квадрати катетів у прямокутному трикутнику, отримаємо квадрат гіпотенузи. Як видно з формули, цей вираз знаходиться під коренем. Обчисливши корінь із квадрата гіпотенузи, ми отримаємо саму довжину. Множення виразу, що вийшов, на 1/2 в результаті призводить нас до виразу 1/2 × c = c/2.
Стовпці 1, 2 та 3 відносяться до прямокутних трикутників. Стовпці 2 і 3 дають відповідно найменшу сторону і гіпотенузу кожного трикутника. Колонка 1 дає квадрат відношення по обидва боки правого кута. Наприклад, рядок 5 починається у сексуальній системі.
Це занадто точно, щоб бути правдою, але ви можете перевірити, що це те саме для інших рядків. Існує суперечки щодо методів, які вавилоняни могли використовувати для складання цієї таблиці. Також є помилки в копії переписувача і невеликі таємниці, наприклад рядок 11, який дає як сторони 45 і 1 15, тобто в десятковій нумерації: 45, і обидва вони кратні 15, і цей трикутник - це не що інше, як трикутник сторін . Чому це не дано у цій формі, набагато простіше? І що може бути перевагою, щоб дати квадрат схилу, а не самого схилу?
Приклад: Обчислити радіус описаного кола, якщо катети трикутника дорівнюють 3 і 4. Підставимо значення формулу. Отримаємо: R = 1/2 × √ (3 ² + 4 ²) = 1/2 × √25 = 1/2 × 5 = 2.5.
У цьому виразі 5 — довжина гіпотенузи.
Відповідь: R = 2.5.
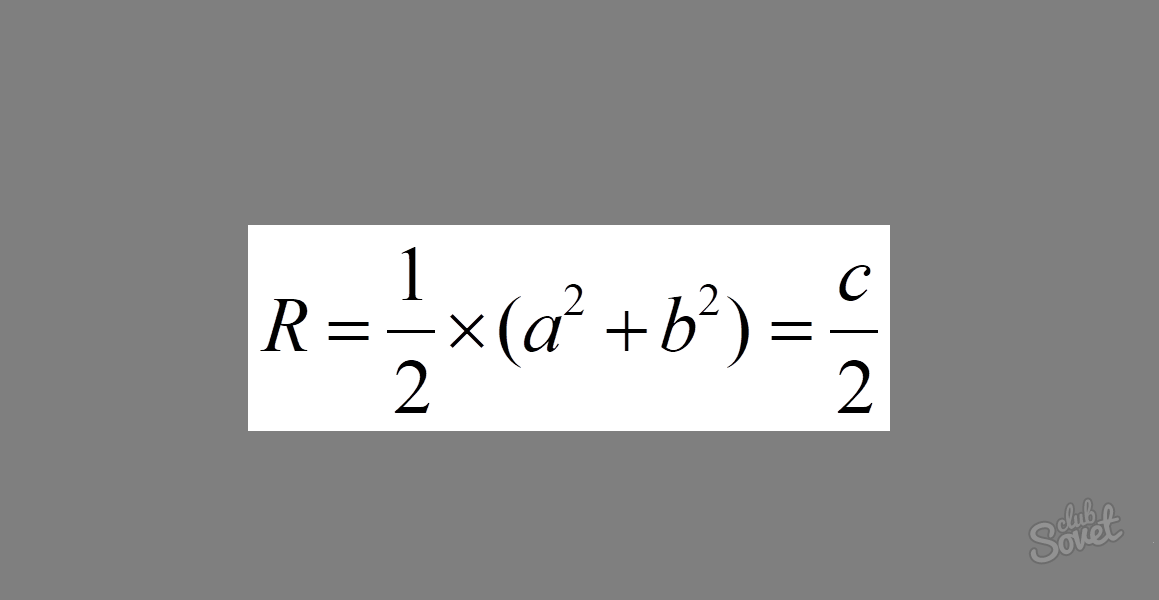
Як знайти радіус кола, описаного біля рівнобедреного трикутника
Формула виглядає так: R = a²/√(4a² — b²), де a — довжина стегна трикутника і b — довжина основи.
Приклад: Обчислити радіус кола, якщо його стегно = 7, а основа = 8.
Рішення: Підставляємо у формулу дані значення та одержуємо: R = 7²/√(4 × 7² — 8²).
R = 49/√(196 - 64) = 49/√132. Відповідь можна записати прямо так.
Відповідь: R = 49/√132
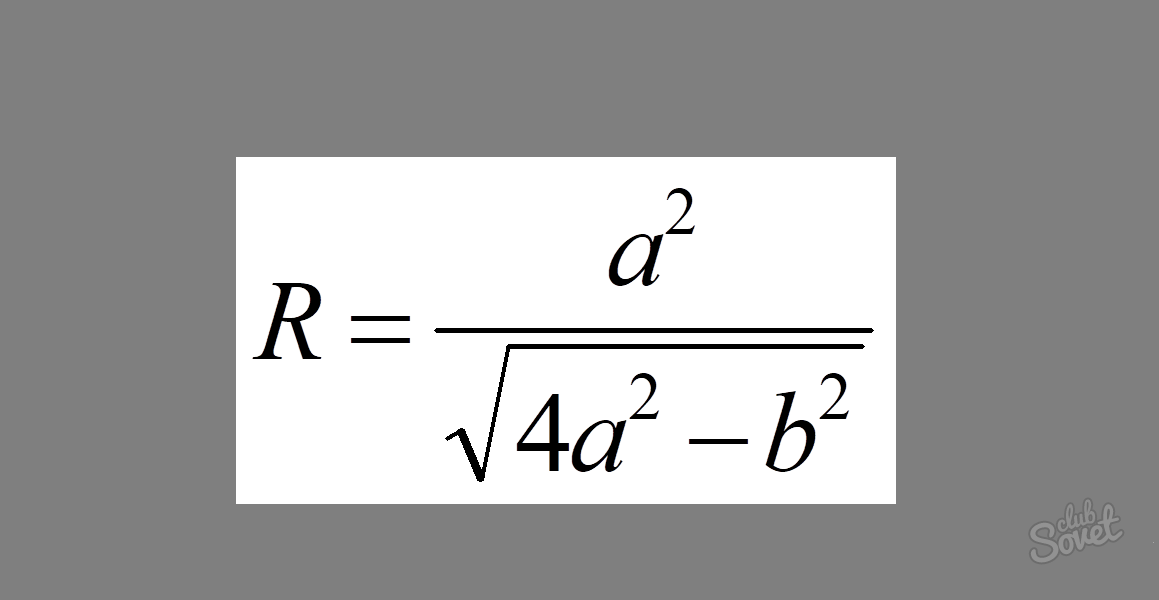
Онлайн ресурси для обчислення радіуса кола
Можна дуже легко заплутатися у всіх цих формулах. Тому за потреби можна скористатися онлайн калькуляторамиякі допоможуть вам у вирішенні завдань на знаходження радіусу. Принцип роботи таких міні-програм дуже простий. Підставляєте значення сторони у відповідне поле та отримуєте готову відповідь. Можна вибрати кілька варіантів заокруглення відповіді: до десяткових, сотих, тисячних і т.д.